
Question Number 21354 by Tinkutara last updated on 21/Sep/17
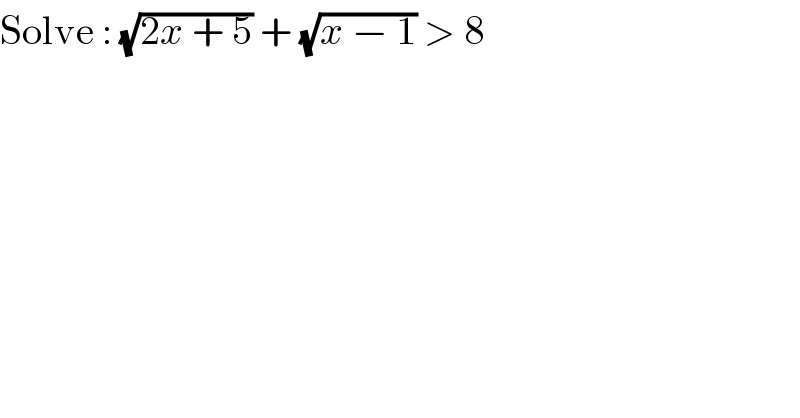
$$\mathrm{Solve}\::\:\sqrt{\mathrm{2}{x}\:+\:\mathrm{5}}\:+\:\sqrt{{x}\:−\:\mathrm{1}}\:>\:\mathrm{8} \\ $$
Commented byTinkutara last updated on 22/Sep/17
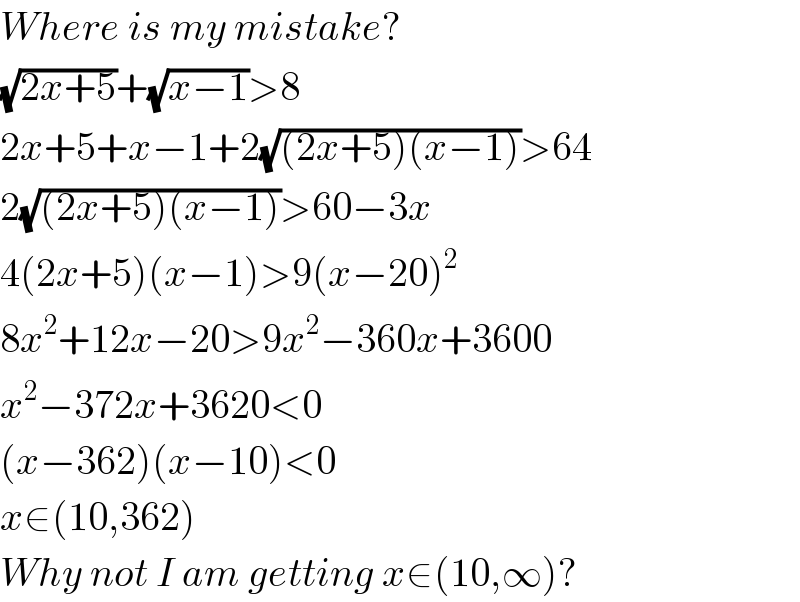
$${Where}\:{is}\:{my}\:{mistake}? \\ $$ $$\sqrt{\mathrm{2}{x}+\mathrm{5}}+\sqrt{{x}−\mathrm{1}}>\mathrm{8} \\ $$ $$\mathrm{2}{x}+\mathrm{5}+{x}−\mathrm{1}+\mathrm{2}\sqrt{\left(\mathrm{2}{x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)}>\mathrm{64} \\ $$ $$\mathrm{2}\sqrt{\left(\mathrm{2}{x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)}>\mathrm{60}−\mathrm{3}{x} \\ $$ $$\mathrm{4}\left(\mathrm{2}{x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)>\mathrm{9}\left({x}−\mathrm{20}\right)^{\mathrm{2}} \\ $$ $$\mathrm{8}{x}^{\mathrm{2}} +\mathrm{12}{x}−\mathrm{20}>\mathrm{9}{x}^{\mathrm{2}} −\mathrm{360}{x}+\mathrm{3600} \\ $$ $${x}^{\mathrm{2}} −\mathrm{372}{x}+\mathrm{3620}<\mathrm{0} \\ $$ $$\left({x}−\mathrm{362}\right)\left({x}−\mathrm{10}\right)<\mathrm{0} \\ $$ $${x}\in\left(\mathrm{10},\mathrm{362}\right) \\ $$ $${Why}\:{not}\:{I}\:{am}\:{getting}\:{x}\in\left(\mathrm{10},\infty\right)? \\ $$
Commented byalex041103 last updated on 22/Sep/17
![Ok. First lets consider the folowing Let x<y if we square both sides we get x^2 <y^2 , but x<y→−x>−y→(−x)^2 >(−y)^2 or x^2 >y^2 →contradiction. Before we explore why this is a problem let′s consider an easier case: −x>2⇒x<−2(not >) We know that we reverse the signs. Squaring both sides of the inequality is similar to multiplying both sides by −1 (or taking the reciprical of both sides). So let′s consider the general case: if g(x)≷h(x) then f(g(x)) ≷ or ≶ f(h(x) for some function f(x)≠const. Let s=sgn((d/dx)f(x))=const. for some x∈I where [g(x),h(x)]∈I (suppose there is such I), then { ((f(g(x))≷f(h(x)), s=1)),((f(g(x))≶f(h(x)), s=−1)) :} In conclusion we do reverse the inequality g≷h if (d/dx)f(x)<0 for x∈[g,h] and we don′t if (d/dx)f(x)>0 for x∈[g,h] In our case of f(x)=x^2 sgn((d/dx)f(x))=sgn(x) So in order to be even able to square both sides the sign of both sides must be the same. In the case of (√(2x+5))+(√(x−1))>8 for x∈[1,∞], sgn((√(2x+5))+(√(x−1)))=sgn(8)=1 ⇒ There is no problem in squaring and we don′t reverse the inequality But for 2(√((2x+5)(x−1)))>60−3x sgn(LHS)=1 and sgn(60−3x)=1 or −1 When x∈(20,∞), sgn(60−3x)=−1 and then 0>60−3x and 2(√((2x+5)(x−1)))>0 ⇒x∈(20,∞) then 2(√((2x+5)(x−1)))>60−3x When x∈(1, 20) (starting from one in order for the square root to be real) sgn(60−3x)=1 Then as in your solution we see that for x∈(1,20),x∈(10,362) or x∈[10,20](the ineq. is true for x=20,10) ⇒Ans. x∈[10,∞)](Q21385.png)
$${Ok}.\:{First}\:{lets}\:{consider}\:{the}\:{folowing} \\ $$ $${Let} \\ $$ $${x}<{y} \\ $$ $${if}\:{we}\:{square}\:{both}\:{sides}\:{we}\:{get} \\ $$ $${x}^{\mathrm{2}} <{y}^{\mathrm{2}} ,\:{but} \\ $$ $${x}<{y}\rightarrow−{x}>−{y}\rightarrow\left(−{x}\right)^{\mathrm{2}} >\left(−{y}\right)^{\mathrm{2}} \\ $$ $${or}\:{x}^{\mathrm{2}} >{y}^{\mathrm{2}} \rightarrow{contradiction}. \\ $$ $${Before}\:{we}\:{explore}\:{why}\:{this}\:{is}\:{a}\:{problem} \\ $$ $${let}'{s}\:{consider}\:{an}\:{easier}\:{case}: \\ $$ $$−{x}>\mathrm{2}\Rightarrow{x}<−\mathrm{2}\left({not}\:>\right) \\ $$ $${We}\:{know}\:{that}\:{we}\:{reverse}\:{the}\:{signs}. \\ $$ $${Squaring}\:{both}\:{sides}\:{of}\:{the}\:{inequality} \\ $$ $${is}\:{similar}\:{to}\:{multiplying}\:{both}\:{sides} \\ $$ $${by}\:−\mathrm{1}\:\left({or}\:{taking}\:{the}\:{reciprical}\:{of}\:{both}\right. \\ $$ $$\left.{sides}\right). \\ $$ $${So}\:{let}'{s}\:{consider}\:{the}\:{general}\:{case}: \\ $$ $${if}\:{g}\left({x}\right)\gtrless{h}\left({x}\right)\:{then}\:{f}\left({g}\left({x}\right)\right)\:\gtrless\:{or}\:\lessgtr\:{f}\left({h}\left({x}\right)\right. \\ $$ $${for}\:{some}\:{function}\:{f}\left({x}\right)\neq{const}. \\ $$ $${Let}\:{s}={sgn}\left(\frac{{d}}{{dx}}{f}\left({x}\right)\right)={const}.\:{for}\:{some} \\ $$ $${x}\in{I}\:{where}\:\left[{g}\left({x}\right),{h}\left({x}\right)\right]\in{I}\:\left({suppose}\:{there}\right. \\ $$ $$\left.{is}\:{such}\:{I}\right),\:{then}\: \\ $$ $$\begin{cases}{{f}\left({g}\left({x}\right)\right)\gtrless{f}\left({h}\left({x}\right)\right),\:{s}=\mathrm{1}}\\{{f}\left({g}\left({x}\right)\right)\lessgtr{f}\left({h}\left({x}\right)\right),\:{s}=−\mathrm{1}}\end{cases} \\ $$ $${In}\:{conclusion}\:{we}\:{do}\:{reverse}\:{the}\:{inequality} \\ $$ $${g}\gtrless{h}\:{if}\:\:\frac{{d}}{{dx}}{f}\left({x}\right)<\mathrm{0}\:{for}\:{x}\in\left[{g},{h}\right] \\ $$ $${and}\:{we}\:{don}'{t}\:{if}\:\:\frac{{d}}{{dx}}{f}\left({x}\right)>\mathrm{0}\:{for}\:{x}\in\left[{g},{h}\right] \\ $$ $${In}\:{our}\:{case}\:{of}\:{f}\left({x}\right)={x}^{\mathrm{2}} \: \\ $$ $${sgn}\left(\frac{{d}}{{dx}}{f}\left({x}\right)\right)={sgn}\left({x}\right) \\ $$ $${So}\:{in}\:{order}\:{to}\:{be}\:{even}\:{able}\:{to}\:{square} \\ $$ $${both}\:{sides}\:{the}\:{sign}\:{of}\:{both}\:{sides}\:{must} \\ $$ $${be}\:{the}\:{same}. \\ $$ $${In}\:{the}\:{case}\:{of} \\ $$ $$\sqrt{\mathrm{2}{x}+\mathrm{5}}+\sqrt{{x}−\mathrm{1}}>\mathrm{8} \\ $$ $${for}\:{x}\in\left[\mathrm{1},\infty\right],\:{sgn}\left(\sqrt{\mathrm{2}{x}+\mathrm{5}}+\sqrt{{x}−\mathrm{1}}\right)={sgn}\left(\mathrm{8}\right)=\mathrm{1} \\ $$ $$\Rightarrow\:{There}\:{is}\:{no}\:{problem}\:{in}\:{squaring}\: \\ $$ $${and}\:{we}\:{don}'{t}\:{reverse}\:{the}\:{inequality} \\ $$ $${But}\:{for}\:\mathrm{2}\sqrt{\left(\mathrm{2}{x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)}>\mathrm{60}−\mathrm{3}{x} \\ $$ $${sgn}\left({LHS}\right)=\mathrm{1}\:{and}\:{sgn}\left(\mathrm{60}−\mathrm{3}{x}\right)=\mathrm{1}\:{or}\:−\mathrm{1} \\ $$ $${When}\:{x}\in\left(\mathrm{20},\infty\right),\:{sgn}\left(\mathrm{60}−\mathrm{3}{x}\right)=−\mathrm{1} \\ $$ $${and}\:{then}\:\mathrm{0}>\mathrm{60}−\mathrm{3}{x}\:{and}\:\mathrm{2}\sqrt{\left(\mathrm{2}{x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)}>\mathrm{0} \\ $$ $$\Rightarrow{x}\in\left(\mathrm{20},\infty\right)\:{then}\:\mathrm{2}\sqrt{\left(\mathrm{2}{x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)}>\mathrm{60}−\mathrm{3}{x} \\ $$ $${When}\:{x}\in\left(\mathrm{1},\:\mathrm{20}\right)\:\left({starting}\:{from}\:{one}\right. \\ $$ $$\left.{in}\:{order}\:{for}\:{the}\:{square}\:{root}\:{to}\:{be}\:{real}\right) \\ $$ $${sgn}\left(\mathrm{60}−\mathrm{3}{x}\right)=\mathrm{1} \\ $$ $${Then}\:{as}\:{in}\:{your}\:{solution} \\ $$ $${we}\:{see}\:{that}\:{for}\:{x}\in\left(\mathrm{1},\mathrm{20}\right),{x}\in\left(\mathrm{10},\mathrm{362}\right) \\ $$ $${or}\:{x}\in\left[\mathrm{10},\mathrm{20}\right]\left({the}\:{ineq}.\:{is}\:{true}\:{for}\:{x}=\mathrm{20},\mathrm{10}\right) \\ $$ $$\Rightarrow{Ans}.\:{x}\in\left[\mathrm{10},\infty\right) \\ $$
Commented byTinkutara last updated on 22/Sep/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented byalex041103 last updated on 22/Sep/17
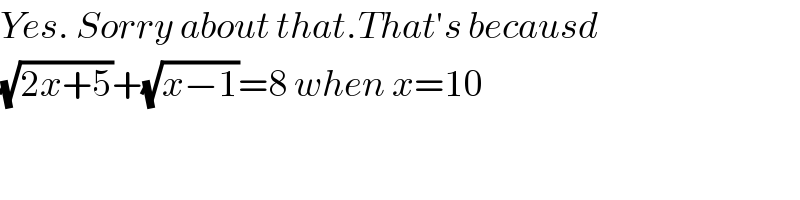
$${Yes}.\:{Sorry}\:{about}\:{that}.{That}'{s}\:{becausd} \\ $$ $$\sqrt{\mathrm{2}{x}+\mathrm{5}}+\sqrt{{x}−\mathrm{1}}=\mathrm{8}\:{when}\:{x}=\mathrm{10} \\ $$
