Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 21423 by Tinkutara last updated on 23/Sep/17

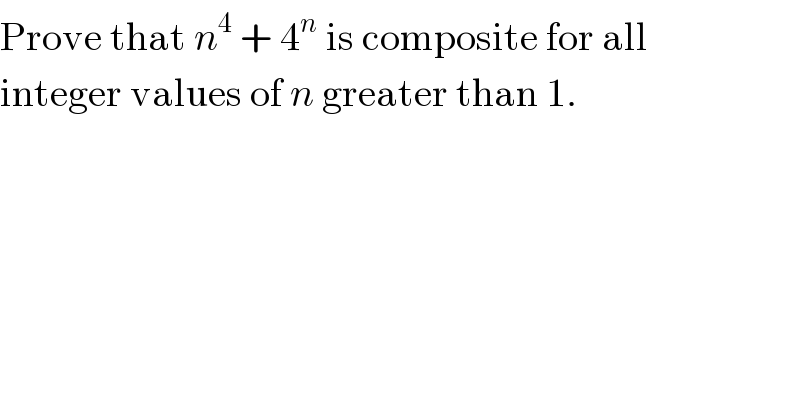
Prove that n^4 + 4^n is composite for all integer values of n greater than 1.

$$\mathrm{Prove}\:\mathrm{that}\:{n}^{\mathrm{4}} \:+\:\mathrm{4}^{{n}} \:\mathrm{is}\:\mathrm{composite}\:\mathrm{for}\:\mathrm{all} \\ $$$$\mathrm{integer}\:\mathrm{values}\:\mathrm{of}\:{n}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{1}. \\ $$

Answered by dioph last updated on 24/Sep/17

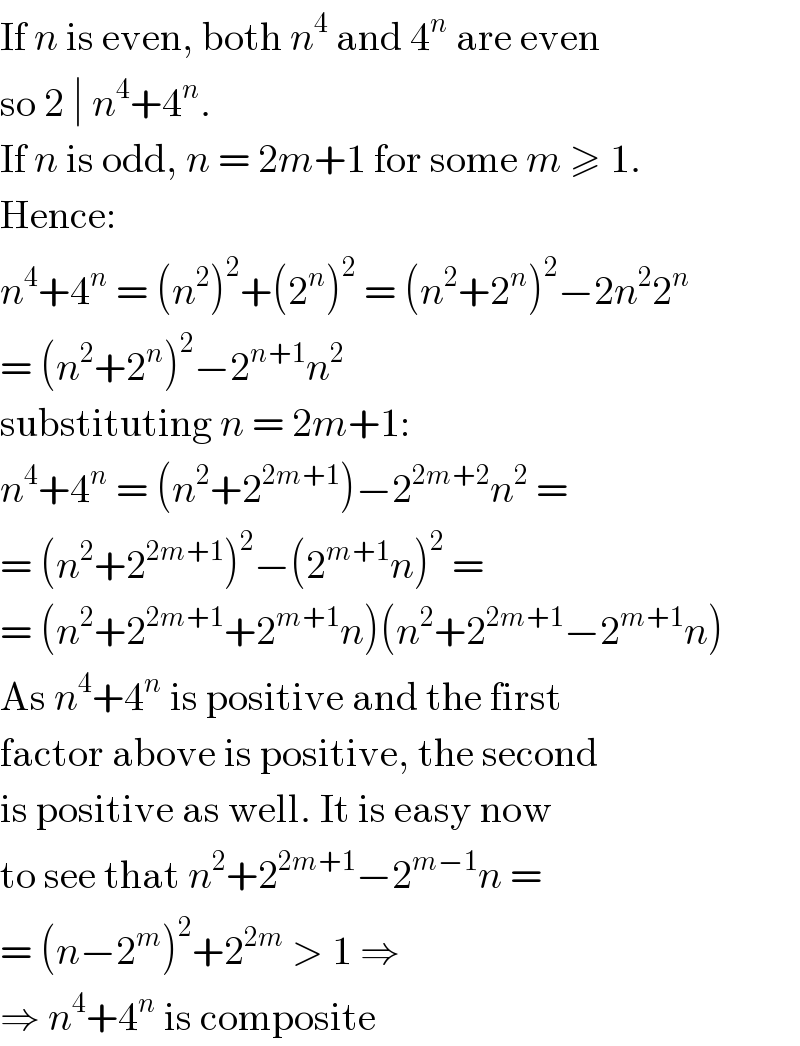
If n is even, both n^4 and 4^n are even so 2 ∣ n^4 +4^n . If n is odd, n = 2m+1 for some m ≥ 1. Hence: n^4 +4^n = (n^2 )^2 +(2^n )^2 = (n^2 +2^n )^2 −2n^2 2^n = (n^2 +2^n )^2 −2^(n+1) n^2 substituting n = 2m+1: n^4 +4^n = (n^2 +2^(2m+1) )−2^(2m+2) n^2 = = (n^2 +2^(2m+1) )^2 −(2^(m+1) n)^2 = = (n^2 +2^(2m+1) +2^(m+1) n)(n^2 +2^(2m+1) −2^(m+1) n) As n^4 +4^n is positive and the first factor above is positive, the second is positive as well. It is easy now to see that n^2 +2^(2m+1) −2^(m−1) n = = (n−2^m )^2 +2^(2m) > 1 ⇒ ⇒ n^4 +4^n is composite

$$\mathrm{If}\:{n}\:\mathrm{is}\:\mathrm{even},\:\mathrm{both}\:{n}^{\mathrm{4}} \:\mathrm{and}\:\mathrm{4}^{{n}} \:\mathrm{are}\:\mathrm{even} \\ $$$$\mathrm{so}\:\mathrm{2}\:\mid\:{n}^{\mathrm{4}} +\mathrm{4}^{{n}} . \\ $$$$\mathrm{If}\:{n}\:\mathrm{is}\:\mathrm{odd},\:{n}\:=\:\mathrm{2}{m}+\mathrm{1}\:\mathrm{for}\:\mathrm{some}\:{m}\:\geqslant\:\mathrm{1}. \\ $$$$\mathrm{Hence}: \\ $$$${n}^{\mathrm{4}} +\mathrm{4}^{{n}} \:=\:\left({n}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{2}^{{n}} \right)^{\mathrm{2}} \:=\:\left({n}^{\mathrm{2}} +\mathrm{2}^{{n}} \right)^{\mathrm{2}} −\mathrm{2}{n}^{\mathrm{2}} \mathrm{2}^{{n}} \\ $$$$=\:\left({n}^{\mathrm{2}} +\mathrm{2}^{{n}} \right)^{\mathrm{2}} −\mathrm{2}^{{n}+\mathrm{1}} {n}^{\mathrm{2}} \\ $$$$\mathrm{substituting}\:{n}\:=\:\mathrm{2}{m}+\mathrm{1}: \\ $$$${n}^{\mathrm{4}} +\mathrm{4}^{{n}} \:=\:\left({n}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{m}+\mathrm{1}} \right)−\mathrm{2}^{\mathrm{2}{m}+\mathrm{2}} {n}^{\mathrm{2}} \:=\: \\ $$$$=\:\left({n}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{m}+\mathrm{1}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{{m}+\mathrm{1}} {n}\right)^{\mathrm{2}} \:= \\ $$$$=\:\left({n}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{m}+\mathrm{1}} +\mathrm{2}^{{m}+\mathrm{1}} {n}\right)\left({n}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{m}+\mathrm{1}} −\mathrm{2}^{{m}+\mathrm{1}} {n}\right) \\ $$$$\mathrm{As}\:{n}^{\mathrm{4}} +\mathrm{4}^{{n}} \:\mathrm{is}\:\mathrm{positive}\:\mathrm{and}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{factor}\:\mathrm{above}\:\mathrm{is}\:\mathrm{positive},\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{is}\:\mathrm{positive}\:\mathrm{as}\:\mathrm{well}.\:\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{now} \\ $$$$\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:{n}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{m}+\mathrm{1}} −\mathrm{2}^{{m}−\mathrm{1}} {n}\:= \\ $$$$=\:\left({n}−\mathrm{2}^{{m}} \right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}{m}} \:>\:\mathrm{1}\:\Rightarrow \\ $$$$\Rightarrow\:{n}^{\mathrm{4}} +\mathrm{4}^{{n}} \:\mathrm{is}\:\mathrm{composite} \\ $$

Commented by Tinkutara last updated on 25/Sep/17

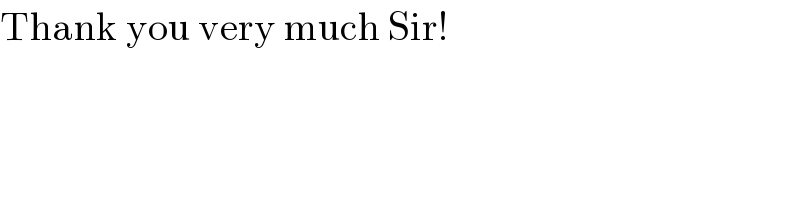
Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com