
Question Number 21503 by mondodotto@gmail.com last updated on 25/Sep/17

Answered by $@ty@m last updated on 26/Sep/17
![Let 4x^2 =t ⇒8xdx=dt Change of limits: As x→4, t→64 As x→y, t→4y^2 I=∫_(64) ^(4y^2 ) (√(1−t))(dt/8) ATQ, 0=(1/8)∫_(64) ^(4y^2 ) (√(1−t))dt 0=[((2(1−t)^(3/2) )/3)]_(64) ^(4y^2 ) (1−4y^2 )^(3/2) −(−63)^(3/2) =0 (1−4y^2 )^(3/2) =(−63)^(3/2) 1−4y^2 =−63 4y^2 =64 y=±4](Q21511.png)
$${Let}\:\mathrm{4}{x}^{\mathrm{2}} ={t} \\ $$$$\Rightarrow\mathrm{8}{xdx}={dt} \\ $$$${Change}\:{of}\:{limits}: \\ $$$${As}\:{x}\rightarrow\mathrm{4},\:{t}\rightarrow\mathrm{64} \\ $$$${As}\:{x}\rightarrow{y},\:{t}\rightarrow\mathrm{4}{y}^{\mathrm{2}} \\ $$$${I}=\underset{\mathrm{64}} {\overset{\mathrm{4}{y}^{\mathrm{2}} } {\int}}\sqrt{\mathrm{1}−{t}}\frac{{dt}}{\mathrm{8}} \\ $$$${ATQ},\:\:\:\mathrm{0}=\frac{\mathrm{1}}{\mathrm{8}}\underset{\mathrm{64}} {\overset{\mathrm{4}{y}^{\mathrm{2}} } {\int}}\sqrt{\mathrm{1}−{t}}{dt} \\ $$$$\mathrm{0}=\left[\frac{\mathrm{2}\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}\right]_{\mathrm{64}} ^{\mathrm{4}{y}^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(−\mathrm{63}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{0} \\ $$$$\left(\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\left(−\mathrm{63}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{1}−\mathrm{4}{y}^{\mathrm{2}} =−\mathrm{63} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} =\mathrm{64} \\ $$$${y}=\pm\mathrm{4} \\ $$
Commented by mrW1 last updated on 26/Sep/17
![1−4x^2 ≥0 ⇒x^2 ≤(1/4) ⇒−(1/2)≤x≤(1/2) i.e. function x(√(1−4x^2 )) is defined only for x∈[−(1/2),(1/2)].](Q21515.png)
$$\mathrm{1}−\mathrm{4x}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \leqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{function}\:\mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{defined}\:\mathrm{only}\:\mathrm{for} \\ $$$$\mathrm{x}\in\left[−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right]. \\ $$
Commented by $@ty@m last updated on 26/Sep/17
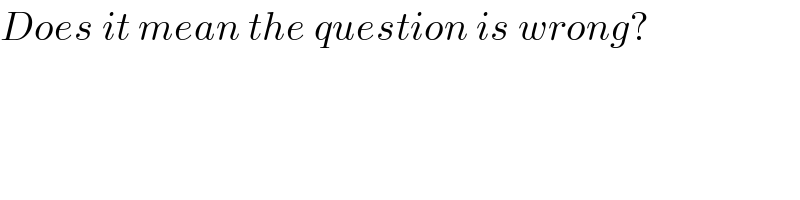
$${Does}\:{it}\:{mean}\:{the}\:{question}\:{is}\:{wrong}? \\ $$
Commented by mrW1 last updated on 26/Sep/17

$$\mathrm{yes} \\ $$
Commented by abwayh last updated on 26/Sep/17
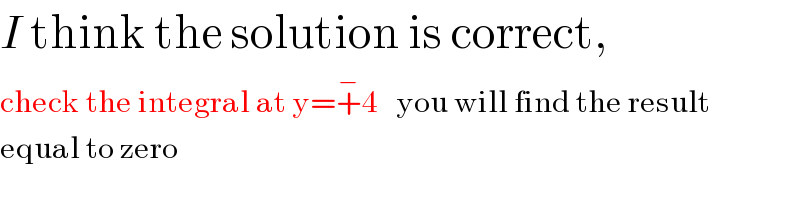
$${I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{correct}, \\ $$$$\mathrm{check}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{at}\:\mathrm{y}=\overset{−} {+}\mathrm{4}\:\:\:\mathrm{you}\:\mathrm{will}\:\mathrm{find}\:\mathrm{the}\:\mathrm{result} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{zero} \\ $$
Commented by mrW1 last updated on 26/Sep/17
![as for the definition of definite integral ∫_a ^( b) f(x), the function f(x) must be continuous on the interval [a, b]. but x(√(1−4x^2 )) is not defined on [−4, −(1/2)] and [(1/2), 4]. so ∫_(−4) ^( −(1/2)) x(√(1−4x^2 )) dx and ∫_(1/2) ^( 4) x(√(1−4x^2 )) dx are also not defined. ∫_(−4) ^( 4) x(√(1−4x^2 )) dx is also not defined, since ∫_(−4) ^( 4) x(√(1−4x^2 )) dx=∫_(−4) ^( −(1/2)) x(√(1−4x^2 )) dx +∫_(−(1/2)) ^( (1/2)) x(√(1−4x^2 )) dx+ ∫_(1/2) ^( 4) x(√(1−4x^2 )) dx](Q21539.png)
$$\mathrm{as}\:\mathrm{for}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{definite} \\ $$$$\mathrm{integral}\:\int_{\mathrm{a}} ^{\:\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right),\:\mathrm{the}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{must} \\ $$$$\mathrm{be}\:\mathrm{continuous}\:\mathrm{on}\:\mathrm{the}\:\mathrm{interval}\:\left[\mathrm{a},\:\mathrm{b}\right]. \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{on}\: \\ $$$$\left[−\mathrm{4},\:−\frac{\mathrm{1}}{\mathrm{2}}\right]\:\mathrm{and}\:\left[\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{4}\right].\:\mathrm{so} \\ $$$$\int_{−\mathrm{4}} ^{\:−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx}\:\mathrm{and}\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\:\mathrm{4}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\mathrm{are}\:\mathrm{also}\:\mathrm{not}\:\mathrm{defined}. \\ $$$$ \\ $$$$\int_{−\mathrm{4}} ^{\:\mathrm{4}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx}\:\mathrm{is}\:\mathrm{also}\:\mathrm{not}\:\mathrm{defined},\:\mathrm{since} \\ $$$$\int_{−\mathrm{4}} ^{\:\mathrm{4}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx}=\int_{−\mathrm{4}} ^{\:−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx}\:+\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx}+\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\:\mathrm{4}} \mathrm{x}\sqrt{\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$
Commented by abwayh last updated on 26/Sep/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir};\mathrm{I}^{'} \mathrm{m}\:\mathrm{understand} \\ $$
