
Question and Answers Forum
Question Number 215640 by BaliramKumar last updated on 12/Jan/25
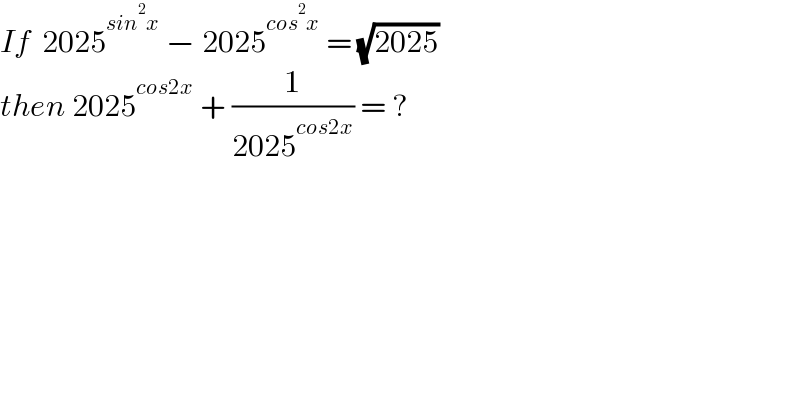
Answered by Frix last updated on 13/Jan/25
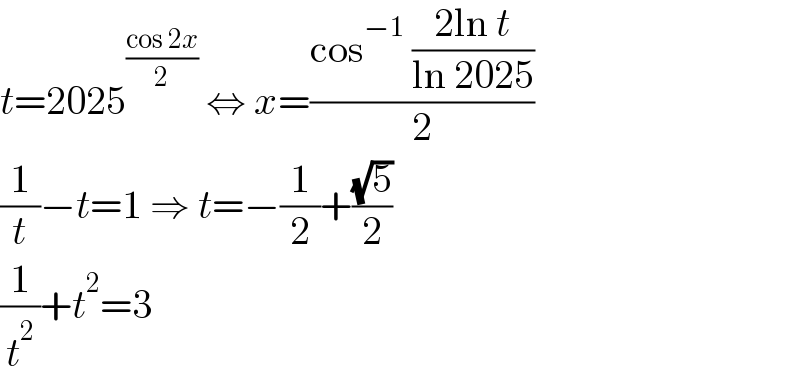
Answered by som(math1967) last updated on 13/Jan/25
![2025^((1−cox2x)/2) −2025^((1+cox2x)/2) =(√(2025)) ⇒(√(2025))[2025^(−((cos2x)/2)) −2025^((cos2x)/2) ]=(√(2025)) ⇒[2025^(−((cos2x)/2)) −2025^((cos2x)/2) ]^2 =1^2 ⇒2025^(−cos2x) +2025^(cox2x) −2.(2025)^0 =1 ∴2025^(cos2x) +(1/(2025^(cos2x) ))=3](Q215648.png)
| ||
Question and Answers Forum | ||
Question Number 215640 by BaliramKumar last updated on 12/Jan/25 | ||
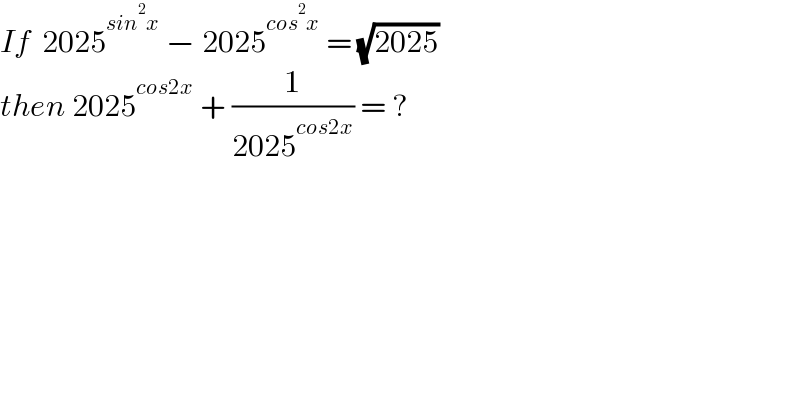 | ||
Answered by Frix last updated on 13/Jan/25 | ||
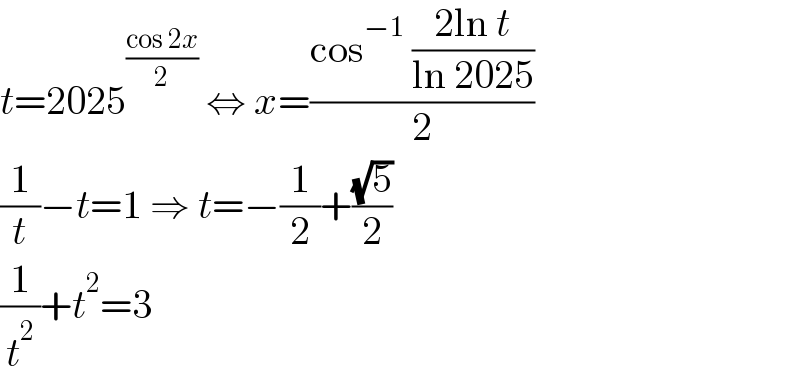 | ||
| ||
Answered by som(math1967) last updated on 13/Jan/25 | ||
![2025^((1−cox2x)/2) −2025^((1+cox2x)/2) =(√(2025)) ⇒(√(2025))[2025^(−((cos2x)/2)) −2025^((cos2x)/2) ]=(√(2025)) ⇒[2025^(−((cos2x)/2)) −2025^((cos2x)/2) ]^2 =1^2 ⇒2025^(−cos2x) +2025^(cox2x) −2.(2025)^0 =1 ∴2025^(cos2x) +(1/(2025^(cos2x) ))=3](Q215648.png) | ||
| ||