Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 21574 by Tinkutara last updated on 27/Sep/17

The cyclic octagon ABCDEFGH has sides a, a, a, a, b, b, b, b respectively. Find the radius of the circle that circumscribes ABCDEFGH in terms of a and b.

$$\mathrm{The}\:\mathrm{cyclic}\:\mathrm{octagon}\:{ABCDEFGH}\:\mathrm{has} \\ $$$$\mathrm{sides}\:{a},\:{a},\:{a},\:{a},\:{b},\:{b},\:{b},\:{b}\:\mathrm{respectively}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{that} \\ $$$$\mathrm{circumscribes}\:{ABCDEFGH}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:{a}\:\mathrm{and}\:{b}. \\ $$

Answered by mrW1 last updated on 05/Oct/17

8×[sin^(−1) ((a/(2R)))+sin^(−1) ((b/(2R)))]=2π let α=sin^(−1) ((a/(2R))) let β=sin^(−1) ((b/(2R))) ⇒8(α+β)=2π ⇒α+β=(π/4) α=(π/4)−β sin α=((√2)/2)(cos β−sin β) (√2)sin α+sin β=cos β (√2)×(a/(2R))+(b/(2R))=cos β (1/(2R))((√2)a+b)=cos β ((2a^2 +2(√2)ab+b^2 )/(4R^2 ))=cos^2 β=1−sin^2 β=1−(b^2 /(4R^2 )) ((2a^2 +2(√2)ab+2b^2 )/(4R^2 ))=1 ((a^2 +(√2)ab+b^2 )/(2R^2 ))=1 ⇒R=(√((a^2 +b^2 +(√2)ab)/2))

$$\mathrm{8}×\left[\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2R}}\right)+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{2R}}\right)\right]=\mathrm{2}\pi \\ $$$$\mathrm{let}\:\alpha=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2R}}\right) \\ $$$$\mathrm{let}\:\beta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{2R}}\right) \\ $$$$\Rightarrow\mathrm{8}\left(\alpha+\beta\right)=\mathrm{2}\pi \\ $$$$\Rightarrow\alpha+\beta=\frac{\pi}{\mathrm{4}} \\ $$$$\alpha=\frac{\pi}{\mathrm{4}}−\beta \\ $$$$\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{cos}\:\beta−\mathrm{sin}\:\beta\right) \\ $$$$\sqrt{\mathrm{2}}\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta=\mathrm{cos}\:\beta \\ $$$$\sqrt{\mathrm{2}}×\frac{\mathrm{a}}{\mathrm{2R}}+\frac{\mathrm{b}}{\mathrm{2R}}=\mathrm{cos}\:\beta \\ $$$$\frac{\mathrm{1}}{\mathrm{2R}}\left(\sqrt{\mathrm{2}}\mathrm{a}+\mathrm{b}\right)=\mathrm{cos}\:\beta \\ $$$$\frac{\mathrm{2a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\mathrm{ab}+\mathrm{b}^{\mathrm{2}} }{\mathrm{4R}^{\mathrm{2}} }=\mathrm{cos}^{\mathrm{2}} \:\beta=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\beta=\mathrm{1}−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{4R}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}\mathrm{ab}+\mathrm{2b}^{\mathrm{2}} }{\mathrm{4R}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{ab}+\mathrm{b}^{\mathrm{2}} }{\mathrm{2R}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\mathrm{R}=\sqrt{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{ab}}{\mathrm{2}}} \\ $$

Commented by mrW1 last updated on 28/Sep/17

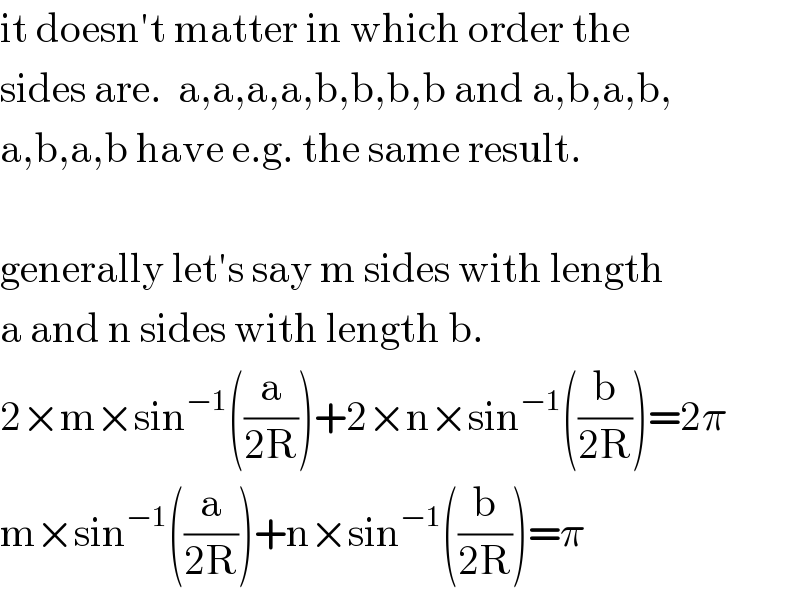
it doesn′t matter in which order the sides are. a,a,a,a,b,b,b,b and a,b,a,b, a,b,a,b have e.g. the same result. generally let′s say m sides with length a and n sides with length b. 2×m×sin^(−1) ((a/(2R)))+2×n×sin^(−1) ((b/(2R)))=2π m×sin^(−1) ((a/(2R)))+n×sin^(−1) ((b/(2R)))=π

$$\mathrm{it}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{matter}\:\mathrm{in}\:\mathrm{which}\:\mathrm{order}\:\mathrm{the} \\ $$$$\mathrm{sides}\:\mathrm{are}.\:\:\mathrm{a},\mathrm{a},\mathrm{a},\mathrm{a},\mathrm{b},\mathrm{b},\mathrm{b},\mathrm{b}\:\mathrm{and}\:\mathrm{a},\mathrm{b},\mathrm{a},\mathrm{b}, \\ $$$$\mathrm{a},\mathrm{b},\mathrm{a},\mathrm{b}\:\mathrm{have}\:\mathrm{e}.\mathrm{g}.\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}. \\ $$$$ \\ $$$$\mathrm{generally}\:\mathrm{let}'\mathrm{s}\:\mathrm{say}\:\mathrm{m}\:\mathrm{sides}\:\mathrm{with}\:\mathrm{length} \\ $$$$\mathrm{a}\:\mathrm{and}\:\mathrm{n}\:\mathrm{sides}\:\mathrm{with}\:\mathrm{length}\:\mathrm{b}. \\ $$$$\mathrm{2}×\mathrm{m}×\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2R}}\right)+\mathrm{2}×\mathrm{n}×\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{2R}}\right)=\mathrm{2}\pi \\ $$$$\mathrm{m}×\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{a}}{\mathrm{2R}}\right)+\mathrm{n}×\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{2R}}\right)=\pi \\ $$

Commented by Tinkutara last updated on 06/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Commented by mrW1 last updated on 05/Oct/17

thank you sir!

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com