Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 2160 by Yozzis last updated on 05/Nov/15

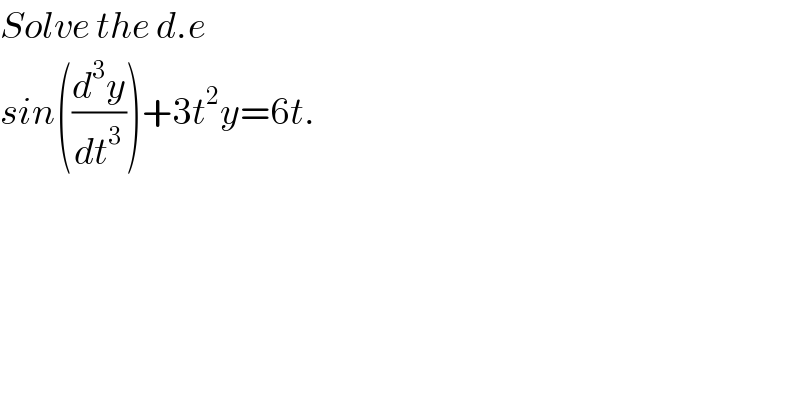
Solve the d.e sin((d^3 y/dt^3 ))+3t^2 y=6t.

$${Solve}\:{the}\:{d}.{e} \\ $$$${sin}\left(\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{3}} }\right)+\mathrm{3}{t}^{\mathrm{2}} {y}=\mathrm{6}{t}. \\ $$

Commented by Yozzi last updated on 07/Nov/15

I was helping a friend with his engineering math homework and he therefore took a picture of the problem. It was a worksheet. I answered the question but but in that picture I saw a number of strange D.Es as part of another exercise. The exercise was to simply identify the type of D.E but I thought, ′How would one solve it or prove it is unsolvable?′ The D.E problem above this problem was also from the set of strange D.Es I saw. Yozzis=Yozzi

$${I}\:{was}\:{helping}\:{a}\:{friend}\:{with}\:{his}\: \\ $$$${engineering}\:{math}\:{homework}\:{and}\: \\ $$$${he}\:{therefore}\:{took}\:{a}\:{picture}\:{of}\:{the}\:{problem}. \\ $$$${It}\:{was}\:{a}\:{worksheet}.\:{I}\:{answered}\:{the}\:{question}\:{but} \\ $$$${but}\:{in}\:{that}\:{picture}\:{I}\:{saw}\:{a}\:{number}\:{of}\: \\ $$$${strange}\:{D}.{Es}\:{as}\:{part}\:{of}\:{another}\:{exercise}.\:{The}\:{exercise}\:{was}\:{to}\:{simply} \\ $$$${identify}\:{the}\:{type}\:{of}\:{D}.{E}\:{but}\:{I}\:{thought}, \\ $$$$'{How}\:{would}\:{one}\:{solve}\:{it}\:{or}\:{prove}\:{it}\:{is} \\ $$$${unsolvable}?'\:{The}\:{D}.{E}\:{problem}\:{above} \\ $$$${this}\:{problem}\:{was}\:{also}\:{from}\:{the}\:{set} \\ $$$${of}\:{strange}\:{D}.{Es}\:{I}\:{saw}. \\ $$$${Yozzis}={Yozzi} \\ $$

Commented by prakash jain last updated on 07/Nov/15

Difficult. Did you come across this while working on physics problem?

$$\mathrm{Difficult}.\:\mathrm{Did}\:\mathrm{you}\:\mathrm{come}\:\mathrm{across}\:\mathrm{this}\:\mathrm{while} \\ $$$$\mathrm{working}\:\mathrm{on}\:\mathrm{physics}\:\mathrm{problem}? \\ $$

Commented by prakash jain last updated on 08/Nov/15

assuming y can be differentiated 4 times cos ((d^3 y/dt^4 ))(d^4 y/dt^4 )=6−6ty−3t^2 (dy/dt) cos ((d^3 y/dt^4 ))=((d^4 y/dt^4 ))^(−1) (6−6ty−3t^2 (dy/dt)) 1=36t^2 +((d^4 y/dt^4 ))^((−2)) (6−6ty−3t^2 (dy/dt))^2 The above equation appears solvable with series expansion.

$${assuming}\:{y}\:{can}\:{be}\:{differentiated}\:\mathrm{4}\:{times} \\ $$$$\mathrm{cos}\:\left(\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{4}} }\right)\frac{{d}^{\mathrm{4}} {y}}{{dt}^{\mathrm{4}} }=\mathrm{6}−\mathrm{6}{ty}−\mathrm{3}{t}^{\mathrm{2}} \:\frac{{dy}}{{dt}} \\ $$$$\mathrm{cos}\:\left(\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{4}} }\right)=\left(\frac{{d}^{\mathrm{4}} {y}}{{dt}^{\mathrm{4}} }\right)^{−\mathrm{1}} \left(\mathrm{6}−\mathrm{6}{ty}−\mathrm{3}{t}^{\mathrm{2}} \:\frac{{dy}}{{dt}}\right) \\ $$$$\mathrm{1}=\mathrm{36}{t}^{\mathrm{2}} +\left(\frac{{d}^{\mathrm{4}} {y}}{{dt}^{\mathrm{4}} }\right)^{\left(−\mathrm{2}\right)} \left(\mathrm{6}−\mathrm{6}{ty}−\mathrm{3}{t}^{\mathrm{2}} \frac{{dy}}{{dt}}\right)^{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{above}\:\mathrm{equation}\:\mathrm{appears}\:\mathrm{solvable}\:\mathrm{with} \\ $$$$\mathrm{series}\:\mathrm{expansion}. \\ $$

Answered by prakash jain last updated on 08/Nov/15

Trying with variable substitution to remove sin function of a differnetial. y=(2/t)−(1/(3t^2 ))sin u sin ((d^3 y/dt^3 ))=6t−3t^2 y=6t−6t+sin u (d^3 y/dt^3 )= u computing (d^3 y/dt^3 ) in terms of u and t (dy/dt)=−(2/t^2 )+(2/(3t^3 ))sin u−(1/(3t^2 ))cos u(du/dt) (d^2 y/dt^2 )=(4/t^3 )+(2/(3t^3 ))cos u(du/dt)−(2/t^4 )sin u+(2/(3t^3 ))cos u(du/dt) −(1/(3t^2 ))cos u(d^2 u/dt^2 )+(1/(3t^2 ))sin u((du/dt))^2 =(4/t^3 )+(4/(3t^3 ))cos u(du/dt)−(2/t^4 )sin u−(1/(3t^2 ))cos u(d^2 u/dt^2 )+(1/(3t^2 ))sin u((du/dt))^2 (d^3 y/dt^3 )=−((12)/t^4 )−(4/t^4 )cos u(du/dt)+(4/(3t^3 ))cos u(d^2 u/dt^2 )−(4/(3t^3 ))sin u((du/dt))^2 +(8/t^5 )sin u−(2/t^4 )cos u(du/dt) +(2/(3t^3 ))cos u(d^2 u/dt^3 )+(1/(3t^2 ))sin u((du/dt))−(1/(3t^2 ))cos u(d^3 u/dt^3 ) +(4/t^4 )sin u((du/dt))^2 −(4/(3t^3 ))cos u((du/dt))^3 −(4/(3t^3 ))sin u(2(du/dt))((d^2 u/dt^2 )) we get an equation between t and u. still a very difficult equation

$$\mathrm{Trying}\:\mathrm{with}\:\mathrm{variable}\:\mathrm{substitution} \\ $$$$\mathrm{to}\:\mathrm{remove}\:\mathrm{sin}\:\mathrm{function}\:\mathrm{of}\:\mathrm{a}\:\mathrm{differnetial}. \\ $$$${y}=\frac{\mathrm{2}}{{t}}−\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{sin}\:{u} \\ $$$$\mathrm{sin}\:\left(\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{3}} }\right)=\mathrm{6}{t}−\mathrm{3}{t}^{\mathrm{2}} {y}=\mathrm{6}{t}−\mathrm{6}{t}+\mathrm{sin}\:{u} \\ $$$$\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{3}} }=\:{u} \\ $$$${computing}\:\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{3}} }\:{in}\:{terms}\:{of}\:{u}\:{and}\:{t} \\ $$$$\frac{{dy}}{{dt}}=−\frac{\mathrm{2}}{{t}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{sin}\:{u}−\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{cos}\:{u}\frac{{du}}{{dt}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }=\frac{\mathrm{4}}{{t}^{\mathrm{3}} }+\frac{\mathrm{2}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{cos}\:{u}\frac{{du}}{{dt}}−\frac{\mathrm{2}}{{t}^{\mathrm{4}} }\mathrm{sin}\:{u}+\frac{\mathrm{2}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{cos}\:{u}\frac{{du}}{{dt}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{cos}\:{u}\frac{{d}^{\mathrm{2}} {u}}{{dt}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{sin}\:{u}\left(\frac{{du}}{{dt}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{4}}{{t}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{cos}\:{u}\frac{{du}}{{dt}}−\frac{\mathrm{2}}{{t}^{\mathrm{4}} }\mathrm{sin}\:{u}−\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{cos}\:{u}\frac{{d}^{\mathrm{2}} {u}}{{dt}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{sin}\:{u}\left(\frac{{du}}{{dt}}\right)^{\mathrm{2}} \\ $$$$\frac{{d}^{\mathrm{3}} {y}}{{dt}^{\mathrm{3}} }=−\frac{\mathrm{12}}{{t}^{\mathrm{4}} }−\frac{\mathrm{4}}{{t}^{\mathrm{4}} }\mathrm{cos}\:{u}\frac{{du}}{{dt}}+\frac{\mathrm{4}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{cos}\:{u}\frac{{d}^{\mathrm{2}} {u}}{{dt}^{\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{sin}\:{u}\left(\frac{{du}}{{dt}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{8}}{{t}^{\mathrm{5}} }\mathrm{sin}\:{u}−\frac{\mathrm{2}}{{t}^{\mathrm{4}} }\mathrm{cos}\:{u}\frac{{du}}{{dt}} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{2}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{cos}\:{u}\frac{{d}^{\mathrm{2}} {u}}{{dt}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{sin}\:{u}\left(\frac{{du}}{{dt}}\right)−\frac{\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\mathrm{cos}\:{u}\frac{{d}^{\mathrm{3}} {u}}{{dt}^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:+\frac{\mathrm{4}}{{t}^{\mathrm{4}} }\mathrm{sin}\:{u}\left(\frac{{du}}{{dt}}\right)^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{cos}\:{u}\left(\frac{{du}}{{dt}}\right)^{\mathrm{3}} −\frac{\mathrm{4}}{\mathrm{3}{t}^{\mathrm{3}} }\mathrm{sin}\:{u}\left(\mathrm{2}\frac{{du}}{{dt}}\right)\left(\frac{{d}^{\mathrm{2}} {u}}{{dt}^{\mathrm{2}} }\right) \\ $$$${we}\:{get}\:{an}\:{equation}\:{between}\:{t}\:{and}\:{u}. \\ $$$${still}\:{a}\:{very}\:{difficult}\:{equation} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com