Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 21682 by Tinkutara last updated on 30/Sep/17

Prove that the ten′s digit of any power of 3 is even. [e.g. the ten′s digit of 3^6 = 729 is 2].

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{ten}'\mathrm{s}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{any}\:\mathrm{power} \\ $$$$\mathrm{of}\:\mathrm{3}\:\mathrm{is}\:\mathrm{even}.\:\left[\mathrm{e}.\mathrm{g}.\:\mathrm{the}\:\mathrm{ten}'\mathrm{s}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{3}^{\mathrm{6}} \:=\right. \\ $$$$\left.\mathrm{729}\:\mathrm{is}\:\mathrm{2}\right]. \\ $$

Answered by alex041103 last updated on 30/Sep/17

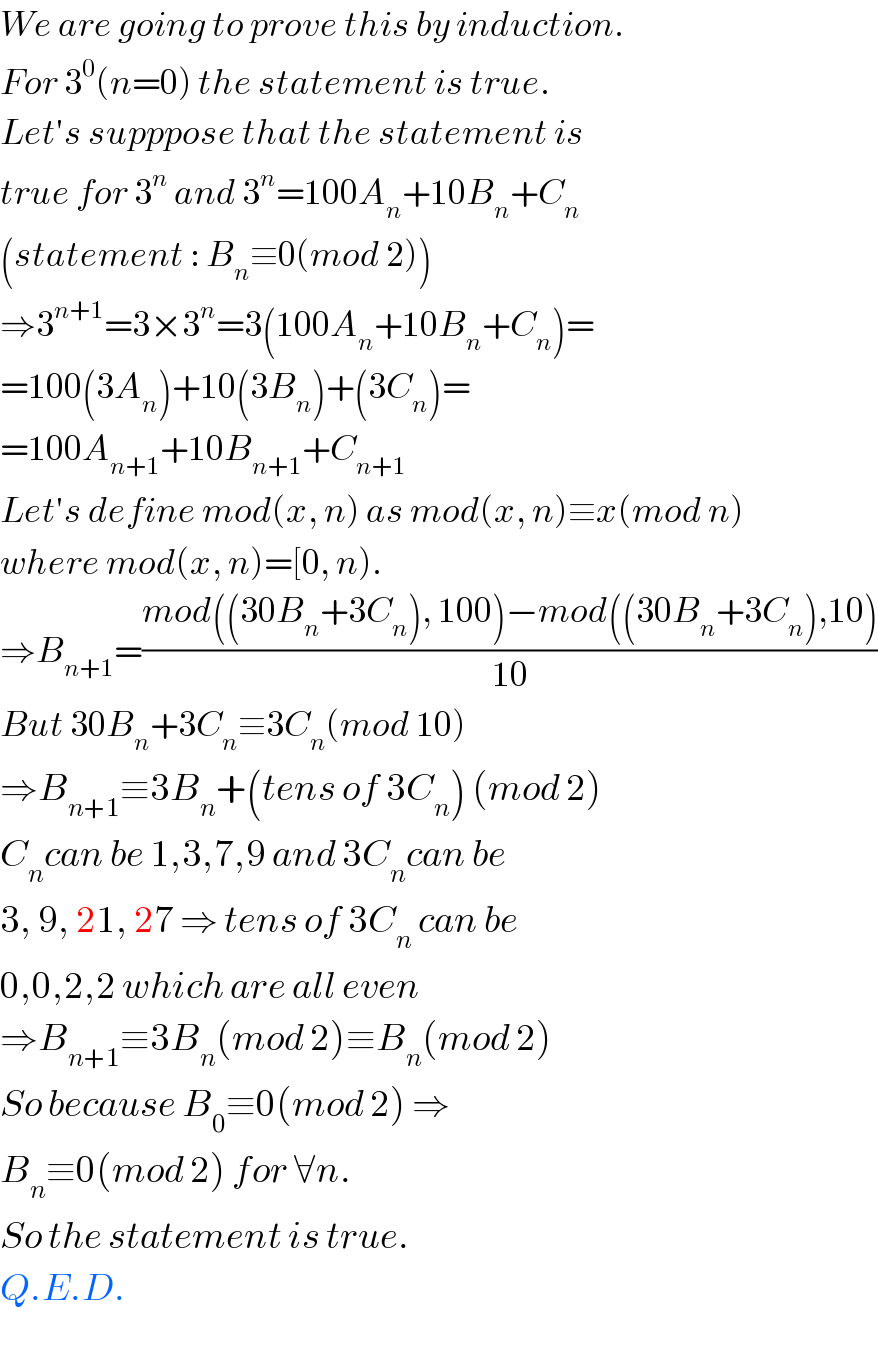
We are going to prove this by induction. For 3^0 (n=0) the statement is true. Let′s supppose that the statement is true for 3^n and 3^n =100A_n +10B_n +C_n (statement : B_n ≡0(mod 2)) ⇒3^(n+1) =3×3^n =3(100A_n +10B_n +C_n )= =100(3A_n )+10(3B_n )+(3C_n )= =100A_(n+1) +10B_(n+1) +C_(n+1) Let′s define mod(x, n) as mod(x, n)≡x(mod n) where mod(x, n)=[0, n). ⇒B_(n+1) =((mod((30B_n +3C_n ), 100)−mod((30B_n +3C_n ),10))/(10)) But 30B_n +3C_n ≡3C_n (mod 10) ⇒B_(n+1) ≡3B_n +(tens of 3C_n ) (mod 2) C_n can be 1,3,7,9 and 3C_n can be 3, 9, 21, 27 ⇒ tens of 3C_n can be 0,0,2,2 which are all even ⇒B_(n+1) ≡3B_n (mod 2)≡B_n (mod 2) So because B_0 ≡0(mod 2) ⇒ B_n ≡0(mod 2) for ∀n. So the statement is true. Q.E.D.

$${We}\:{are}\:{going}\:{to}\:{prove}\:{this}\:{by}\:{induction}. \\ $$$${For}\:\mathrm{3}^{\mathrm{0}} \left({n}=\mathrm{0}\right)\:{the}\:{statement}\:{is}\:{true}. \\ $$$${Let}'{s}\:{supppose}\:{that}\:{the}\:{statement}\:{is} \\ $$$${true}\:{for}\:\mathrm{3}^{{n}} \:{and}\:\mathrm{3}^{{n}} =\mathrm{100}{A}_{{n}} +\mathrm{10}{B}_{{n}} +{C}_{{n}} \\ $$$$\left({statement}\::\:{B}_{{n}} \equiv\mathrm{0}\left({mod}\:\mathrm{2}\right)\right) \\ $$$$\Rightarrow\mathrm{3}^{{n}+\mathrm{1}} =\mathrm{3}×\mathrm{3}^{{n}} =\mathrm{3}\left(\mathrm{100}{A}_{{n}} +\mathrm{10}{B}_{{n}} +{C}_{{n}} \right)= \\ $$$$=\mathrm{100}\left(\mathrm{3}{A}_{{n}} \right)+\mathrm{10}\left(\mathrm{3}{B}_{{n}} \right)+\left(\mathrm{3}{C}_{{n}} \right)= \\ $$$$=\mathrm{100}{A}_{{n}+\mathrm{1}} +\mathrm{10}{B}_{{n}+\mathrm{1}} +{C}_{{n}+\mathrm{1}} \\ $$$${Let}'{s}\:{define}\:{mod}\left({x},\:{n}\right)\:{as}\:{mod}\left({x},\:{n}\right)\equiv{x}\left({mod}\:{n}\right) \\ $$$${where}\:{mod}\left({x},\:{n}\right)=\left[\mathrm{0},\:{n}\right). \\ $$$$\Rightarrow{B}_{{n}+\mathrm{1}} =\frac{{mod}\left(\left(\mathrm{30}{B}_{{n}} +\mathrm{3}{C}_{{n}} \right),\:\mathrm{100}\right)−{mod}\left(\left(\mathrm{30}{B}_{{n}} +\mathrm{3}{C}_{{n}} \right),\mathrm{10}\right)}{\mathrm{10}} \\ $$$${But}\:\mathrm{30}{B}_{{n}} +\mathrm{3}{C}_{{n}} \equiv\mathrm{3}{C}_{{n}} \left({mod}\:\mathrm{10}\right) \\ $$$$\Rightarrow{B}_{{n}+\mathrm{1}} \equiv\mathrm{3}{B}_{{n}} +\left({tens}\:{of}\:\mathrm{3}{C}_{{n}} \right)\:\left({mod}\:\mathrm{2}\right) \\ $$$${C}_{{n}} {can}\:{be}\:\mathrm{1},\mathrm{3},\mathrm{7},\mathrm{9}\:{and}\:\mathrm{3}{C}_{{n}} {can}\:{be} \\ $$$$\mathrm{3},\:\mathrm{9},\:\mathrm{21},\:\mathrm{27}\:\Rightarrow\:{tens}\:{of}\:\mathrm{3}{C}_{{n}} \:{can}\:{be} \\ $$$$\mathrm{0},\mathrm{0},\mathrm{2},\mathrm{2}\:{which}\:{are}\:{all}\:{even} \\ $$$$\Rightarrow{B}_{{n}+\mathrm{1}} \equiv\mathrm{3}{B}_{{n}} \left({mod}\:\mathrm{2}\right)\equiv{B}_{{n}} \left({mod}\:\mathrm{2}\right) \\ $$$${So}\:{because}\:{B}_{\mathrm{0}} \equiv\mathrm{0}\left({mod}\:\mathrm{2}\right)\:\Rightarrow \\ $$$${B}_{{n}} \equiv\mathrm{0}\left({mod}\:\mathrm{2}\right)\:{for}\:\forall{n}. \\ $$$${So}\:{the}\:{statement}\:{is}\:{true}. \\ $$$${Q}.{E}.{D}. \\ $$

Commented by Tinkutara last updated on 01/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com