Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 21693 by Tinkutara last updated on 01/Oct/17

How many six-digit numbers contain exactly four different digits?

$${How}\:{many}\:{six}-{digit}\:{numbers}\:{contain} \\ $$$${exactly}\:{four}\:{different}\:{digits}? \\ $$

Commented by mrW1 last updated on 02/Oct/17

9 numbers with exactly 1 distinct digits 2511 numbers with exactly 2 distinct digits 58320 numbers with exactly 3 distinct digits 294840 numbers with exactly 4 distinct digits 408240 numbers with exactly 5 distinct digits 136080 numbers with exactly 6 distinct digits Σ 900000 numbers

$$\mathrm{9}\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{distinct}\:\mathrm{digits} \\ $$$$\mathrm{2511}\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{2}\:\mathrm{distinct}\:\mathrm{digits} \\ $$$$\mathrm{58320}\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{3}\:\mathrm{distinct}\:\mathrm{digits} \\ $$$$\mathrm{294840}\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{4}\:\mathrm{distinct}\:\mathrm{digits} \\ $$$$\mathrm{408240}\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{5}\:\mathrm{distinct}\:\mathrm{digits} \\ $$$$\mathrm{136080}\:\mathrm{numbers}\:\mathrm{with}\:\mathrm{exactly}\:\mathrm{6}\:\mathrm{distinct}\:\mathrm{digits} \\ $$$$\Sigma\:\mathrm{900000}\:\mathrm{numbers} \\ $$

Commented by Tinkutara last updated on 02/Oct/17

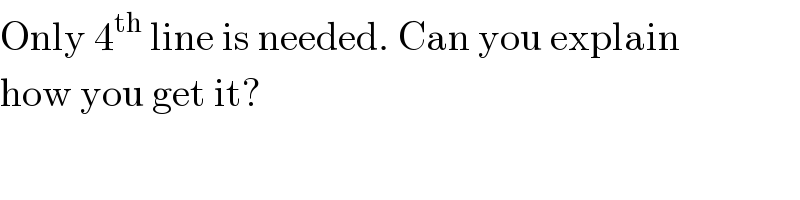
Only 4^(th) line is needed. Can you explain how you get it?

$$\mathrm{Only}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{line}\:\mathrm{is}\:\mathrm{needed}.\:\mathrm{Can}\:\mathrm{you}\:\mathrm{explain} \\ $$$$\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\mathrm{it}? \\ $$

Commented by mrW1 last updated on 05/Oct/17

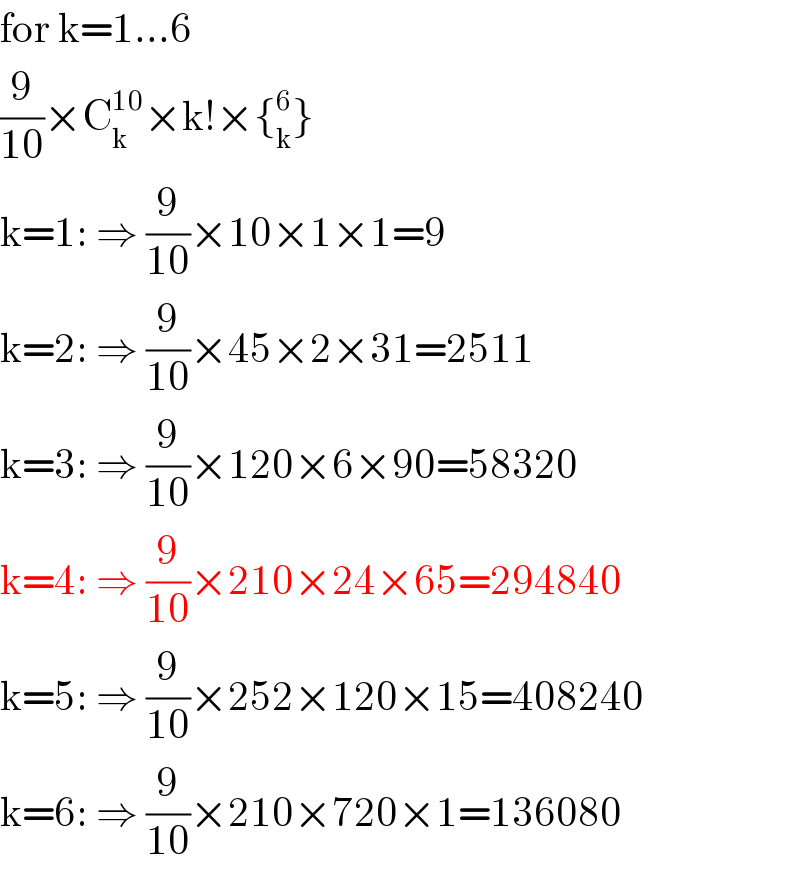
for k=1...6 (9/(10))×C_k ^(10) ×k!×{_k ^6 } k=1: ⇒ (9/(10))×10×1×1=9 k=2: ⇒ (9/(10))×45×2×31=2511 k=3: ⇒ (9/(10))×120×6×90=58320 k=4: ⇒ (9/(10))×210×24×65=294840 k=5: ⇒ (9/(10))×252×120×15=408240 k=6: ⇒ (9/(10))×210×720×1=136080

$$\mathrm{for}\:\mathrm{k}=\mathrm{1}...\mathrm{6} \\ $$$$\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{C}_{\mathrm{k}} ^{\mathrm{10}} ×\mathrm{k}!×\left\{_{\mathrm{k}} ^{\mathrm{6}} \right\} \\ $$$$\mathrm{k}=\mathrm{1}:\:\Rightarrow\:\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{10}×\mathrm{1}×\mathrm{1}=\mathrm{9} \\ $$$$\mathrm{k}=\mathrm{2}:\:\Rightarrow\:\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{45}×\mathrm{2}×\mathrm{31}=\mathrm{2511} \\ $$$$\mathrm{k}=\mathrm{3}:\:\Rightarrow\:\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{120}×\mathrm{6}×\mathrm{90}=\mathrm{58320} \\ $$$$\mathrm{k}=\mathrm{4}:\:\Rightarrow\:\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{210}×\mathrm{24}×\mathrm{65}=\mathrm{294840} \\ $$$$\mathrm{k}=\mathrm{5}:\:\Rightarrow\:\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{252}×\mathrm{120}×\mathrm{15}=\mathrm{408240} \\ $$$$\mathrm{k}=\mathrm{6}:\:\Rightarrow\:\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{210}×\mathrm{720}×\mathrm{1}=\mathrm{136080} \\ $$

Commented by mrW1 last updated on 05/Oct/17

explanation: to select k digits from 10 (incl. 0) there are C_k ^(10) ways to divide 6 positions into k groups there are {_k ^6 } ways, where {} means stirling number of second kind to arrange k digits there are k! ways since digit 0 is not allowed in the first position, the result should be reduced to (9/(10)) ⇒(9/(10))×C_k ^(10) ×k!×{_k ^6 } I worked out this solution by myself, so I′m not sure if it′s correct. pls check.

$$\mathrm{explanation}: \\ $$$$ \\ $$$$\mathrm{to}\:\mathrm{select}\:\mathrm{k}\:\mathrm{digits}\:\mathrm{from}\:\mathrm{10}\:\left(\mathrm{incl}.\:\mathrm{0}\right)\:\mathrm{there} \\ $$$$\mathrm{are}\:\mathrm{C}_{\mathrm{k}} ^{\mathrm{10}} \:\mathrm{ways} \\ $$$$ \\ $$$$\mathrm{to}\:\mathrm{divide}\:\mathrm{6}\:\mathrm{positions}\:\mathrm{into}\:\mathrm{k}\:\mathrm{groups}\:\mathrm{there} \\ $$$$\mathrm{are}\:\left\{_{\mathrm{k}} ^{\mathrm{6}} \right\}\:\mathrm{ways},\:\mathrm{where}\:\left\{\right\}\:\mathrm{means}\:\mathrm{stirling} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{second}\:\mathrm{kind} \\ $$$$ \\ $$$$\mathrm{to}\:\mathrm{arrange}\:\mathrm{k}\:\mathrm{digits}\:\mathrm{there}\:\mathrm{are}\:\mathrm{k}!\:\mathrm{ways} \\ $$$$ \\ $$$$\mathrm{since}\:\mathrm{digit}\:\mathrm{0}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{position},\:\mathrm{the}\:\mathrm{result}\:\mathrm{should}\:\mathrm{be}\:\mathrm{reduced} \\ $$$$\mathrm{to}\:\frac{\mathrm{9}}{\mathrm{10}} \\ $$$$ \\ $$$$\Rightarrow\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{C}_{\mathrm{k}} ^{\mathrm{10}} ×\mathrm{k}!×\left\{_{\mathrm{k}} ^{\mathrm{6}} \right\} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{worked}\:\mathrm{out}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{by}\:\mathrm{myself}, \\ $$$$\mathrm{so}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{correct}.\:\mathrm{pls}\:\mathrm{check}. \\ $$

Commented by Tinkutara last updated on 05/Oct/17

I don′t know any sterling function.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{any}\:\mathrm{sterling}\:\mathrm{function}. \\ $$

Commented by mrW1 last updated on 05/Oct/17

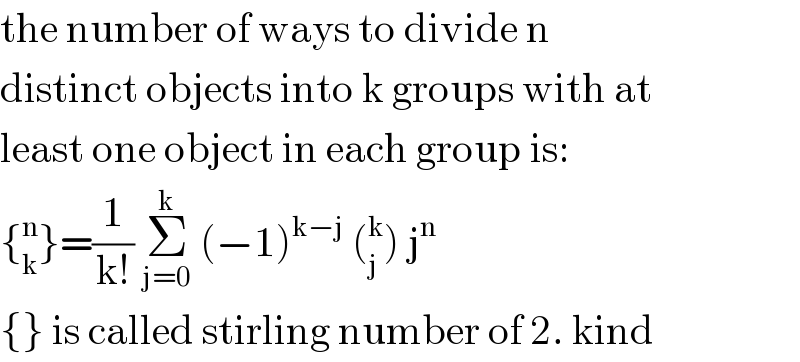
the number of ways to divide n distinct objects into k groups with at least one object in each group is: {_k ^n }=(1/(k!)) Σ_(j=0) ^k (−1)^(k−j) (_j ^k ) j^n {} is called stirling number of 2. kind

$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{divide}\:\mathrm{n} \\ $$$$\mathrm{distinct}\:\mathrm{objects}\:\mathrm{into}\:\mathrm{k}\:\mathrm{groups}\:\mathrm{with}\:\mathrm{at} \\ $$$$\mathrm{least}\:\mathrm{one}\:\mathrm{object}\:\mathrm{in}\:\mathrm{each}\:\mathrm{group}\:\mathrm{is}: \\ $$$$\left\{_{\mathrm{k}} ^{\mathrm{n}} \right\}=\frac{\mathrm{1}}{\mathrm{k}!}\:\underset{\mathrm{j}=\mathrm{0}} {\overset{\mathrm{k}} {\sum}}\:\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{j}} \:\left(_{\mathrm{j}} ^{\mathrm{k}} \right)\:\mathrm{j}^{\mathrm{n}} \\ $$$$\left\{\right\}\:\mathrm{is}\:\mathrm{called}\:\mathrm{stirling}\:\mathrm{number}\:\mathrm{of}\:\mathrm{2}.\:\mathrm{kind} \\ $$

Commented by mrW1 last updated on 05/Oct/17

Commented by Tinkutara last updated on 05/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Commented by mrW1 last updated on 06/Oct/17

what is the solution in your book?

$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{your}\:\mathrm{book}? \\ $$

Commented by Tinkutara last updated on 06/Oct/17

Its very confusing but the one which I understand is:

$$\mathrm{Its}\:\mathrm{very}\:\mathrm{confusing}\:\mathrm{but}\:\mathrm{the}\:\mathrm{one}\:\mathrm{which}\:\mathrm{I} \\ $$$$\mathrm{understand}\:\mathrm{is}: \\ $$

Commented by Tinkutara last updated on 06/Oct/17

Commented by Tinkutara last updated on 06/Oct/17

Commented by Tinkutara last updated on 06/Oct/17

Commented by Tinkutara last updated on 06/Oct/17

Commented by mrW1 last updated on 06/Oct/17

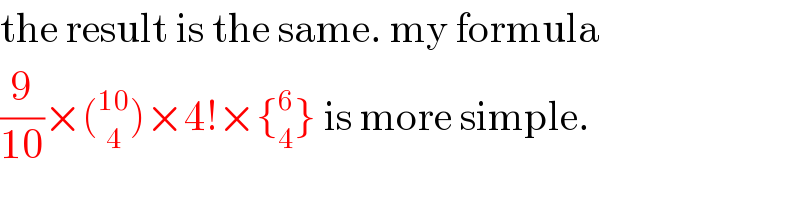
the result is the same. my formula (9/(10))×(_( 4) ^(10) )×4!×{_4 ^6 } is more simple.

$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}.\:\mathrm{my}\:\mathrm{formula} \\ $$$$\frac{\mathrm{9}}{\mathrm{10}}×\left(_{\:\:\mathrm{4}} ^{\mathrm{10}} \right)×\mathrm{4}!×\left\{_{\mathrm{4}} ^{\mathrm{6}} \right\}\:\mathrm{is}\:\mathrm{more}\:\mathrm{simple}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com