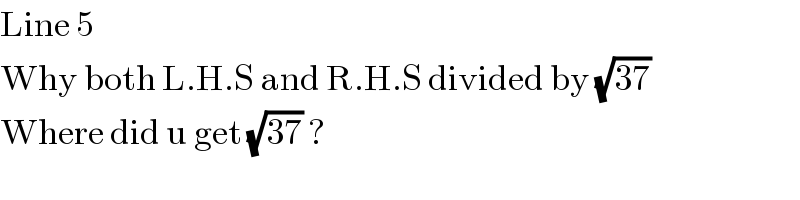Question and Answers Forum
Question Number 21722 by mondodotto@gmail.com last updated on 02/Oct/17

Answered by mrW1 last updated on 02/Oct/17
![cos^2 x+3sin 2x=2 2cos^2 x+6sin 2x=4 2cos^2 x−1+6sin 2x=3 cos 2x+6sin 2x=3 (1/(√(37)))cos 2x+(6/(√(37)))sin 2x=(3/(√(37))) cos α cos 2x+sin α sin 2x=(3/(√(37))) with α=cos^(−1) (1/(√(37))) cos (2x−α)=(3/(√(37))) ⇒2x−α=2nπ±cos^(−1) (3/(√(37))) ⇒x=nπ+(1/2)(α±cos^(−1) (3/(√(37)))) ⇒x=nπ+(1/2)(cos^(−1) (1/(√(37)))±cos^(−1) (3/(√(37)))) in range [0,2π] x=(1/2)(cos^(−1) (1/(√(37)))−cos^(−1) (3/(√(37))))≈10.04° x=(1/2)(cos^(−1) (1/(√(37)))+cos^(−1) (3/(√(37))))≈70.49° x=π+(1/2)(cos^(−1) (1/(√(37)))−cos^(−1) (3/(√(37))))≈190.04° x=π+(1/2)(cos^(−1) (1/(√(37)))+cos^(−1) (3/(√(37))))≈250.49°](Q21736.png)
Commented by mondodotto@gmail.com last updated on 02/Oct/17
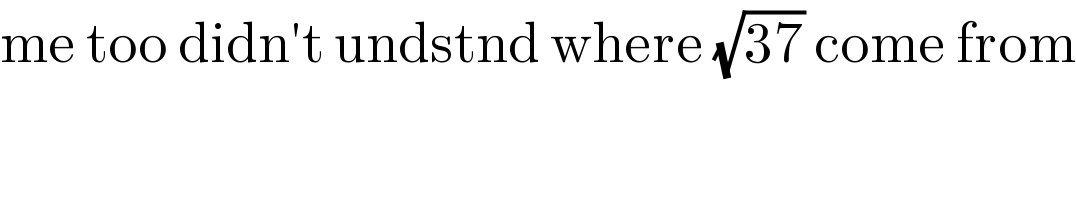
Commented by mrW1 last updated on 02/Oct/17

Commented by Joel577 last updated on 02/Oct/17

Commented by Joel577 last updated on 02/Oct/17