Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 21781 by Tinkutara last updated on 03/Oct/17

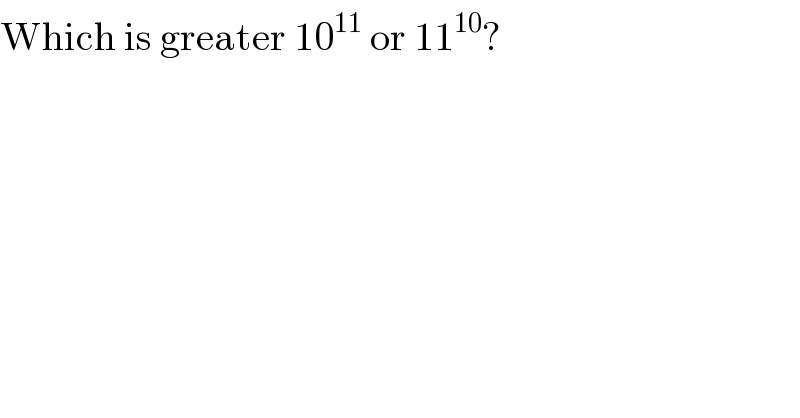
Which is greater 10^(11) or 11^(10) ?

$$\mathrm{Which}\:\mathrm{is}\:\mathrm{greater}\:\mathrm{10}^{\mathrm{11}} \:\mathrm{or}\:\mathrm{11}^{\mathrm{10}} ? \\ $$

Answered by Joel577 last updated on 03/Oct/17

10^(11) ... 11^(10) 11 log 10 ... 10 log 11 11 ... 10 (1.04) 11 > 10.4

$$\:\:\:\:\:\:\:\:\:\:\mathrm{10}^{\mathrm{11}} \:...\:\mathrm{11}^{\mathrm{10}} \\ $$$$\mathrm{11}\:\mathrm{log}\:\mathrm{10}\:...\:\mathrm{10}\:\mathrm{log}\:\mathrm{11} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{11}\:\:...\:\mathrm{10}\:\left(\mathrm{1}.\mathrm{04}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{11}\:\:>\:\mathrm{10}.\mathrm{4} \\ $$

Commented by Tinkutara last updated on 03/Oct/17

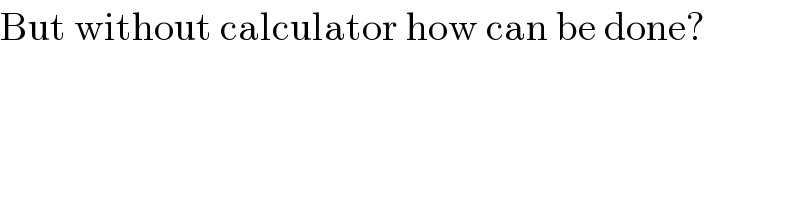
But without calculator how can be done?

$$\mathrm{But}\:\mathrm{without}\:\mathrm{calculator}\:\mathrm{how}\:\mathrm{can}\:\mathrm{be}\:\mathrm{done}? \\ $$

Answered by Bruce Lee last updated on 04/Oct/17

We have this form (n+1)^n <n^(n+1) ;n≥3 proof: for n=3 ⇒ 4^3 <3^4 or 64<81 true assum that it true till n=k we get (k+1)^k <k^(k+1) we wish to prove that (k+2)^(k+1) <(k+1)^(k+2ww) k^(k+1) >(k+1)^k ⇒k^(k+1) ∙(((k+1)^(k+2) )/k^(k+1) )>(k+1)^k ∙(((k+1)^(k+2) )/k^(k+1) ) (k+1)^(k+2) >(((k+1)^(2k+2) )/k^(k+1) ) (k+1)^(k+2) >(((k^2 +2k+1)^(k+1) )/k^(k+1) ) (k+1)^(k+2) >(k+2+(1/k))^(k+1) >(k+2)^(k+1) ⇒(k+2)^(k+1) <(k+1)^(k+2) ⇒(n+1)^n <n^(n+1)

$$\boldsymbol{\mathrm{We}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{form}}\:\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} <\boldsymbol{\mathrm{n}}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \:;\boldsymbol{\mathrm{n}}\geqslant\mathrm{3} \\ $$$$\boldsymbol{\mathrm{proof}}: \\ $$$$\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{n}}=\mathrm{3}\:\Rightarrow\:\mathrm{4}^{\mathrm{3}} <\mathrm{3}^{\mathrm{4}} \:{or}\:\mathrm{64}<\mathrm{81}\:\:\:\boldsymbol{\mathrm{true}} \\ $$$$\boldsymbol{\mathrm{assum}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{true}}\:\boldsymbol{\mathrm{till}}\:\boldsymbol{\mathrm{n}}=\boldsymbol{\mathrm{k}} \\ $$$$\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}} <\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} \\ $$$$\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{wish}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}}\:\left(\boldsymbol{\mathrm{k}}+\mathrm{2}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{1}} <\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}\boldsymbol{\mathrm{ww}}} \\ $$$$\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} >\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}} \:\:\: \\ $$$$\Rightarrow\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} \centerdot\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}} }{\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} }>\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}} \centerdot\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}} }{\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} } \\ $$$$\:\:\:\:\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}} >\frac{\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\mathrm{2}\boldsymbol{\mathrm{k}}+\mathrm{2}} }{\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} } \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}} >\frac{\left(\boldsymbol{\mathrm{k}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{1}} }{\boldsymbol{\mathrm{k}}^{\boldsymbol{\mathrm{k}}+\mathrm{1}} } \\ $$$$\:\:\:\:\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}} >\left(\boldsymbol{\mathrm{k}}+\mathrm{2}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{k}}}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{1}} >\left(\boldsymbol{\mathrm{k}}+\mathrm{2}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{1}} \\ $$$$\Rightarrow\left(\boldsymbol{\mathrm{k}}+\mathrm{2}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{1}} <\left(\boldsymbol{\mathrm{k}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{k}}+\mathrm{2}} \\ $$$$\Rightarrow\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} <\boldsymbol{\mathrm{n}}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} \\ $$$$ \\ $$

Commented by Tinkutara last updated on 04/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Commented by Joel577 last updated on 04/Oct/17

nice proof Sir

$${nice}\:{proof}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com