Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 21795 by hi147 last updated on 04/Oct/17

help x∈N determine x where 7 divise 2^x +3^x

$${help} \\ $$$${x}\in{N} \\ $$$${determine}\:{x}\:{where}\:\mathrm{7}\:{divise}\:\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 04/Oct/17

x=3,9

$$\mathrm{x}=\mathrm{3},\mathrm{9} \\ $$

Commented by prakash jain last updated on 04/Oct/17

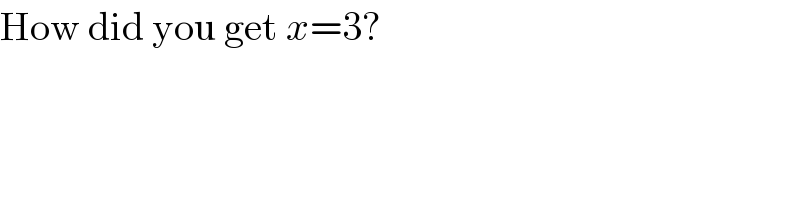
How did you get x=3?

$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:{x}=\mathrm{3}? \\ $$

Commented by math solver last updated on 05/Oct/17

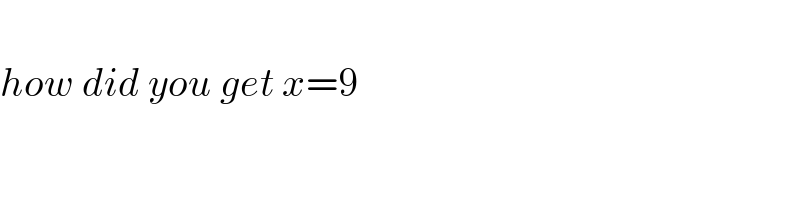
how did you get x=9

$$ \\ $$$${how}\:{did}\:{you}\:{get}\:{x}=\mathrm{9} \\ $$

Answered by mrW1 last updated on 04/Oct/17

x=3^n , n∈N prove: for n=1, 2^3^1 +3^3^1 =8+27=35 mod 7=0 it′s true for n=1. let′s assume it′s true for n, i.e. 2^3^n +3^3^n mod 7=0 for n+1: (2^3^(n+1) +3^3^(n+1) ) mod 7 =(2^(3×3^n ) +3^(3×3^n ) ) mod 7 =[(2^3^n )^3 +(3^3^n )^3 ] mod 7 =[(2^3^n )+(3^3^n )][(2^3^n )^2 −(2^3^n )(3^3^n )+(3^3^n )^2 ] mod 7 =[(2^3^n )+(3^3^n )] mod 7 =0 ⇒x=3^n is a solution

$$\mathrm{x}=\mathrm{3}^{\mathrm{n}} ,\:\mathrm{n}\in\mathrm{N} \\ $$$$ \\ $$$$\mathrm{prove}: \\ $$$$\mathrm{for}\:\mathrm{n}=\mathrm{1}, \\ $$$$\mathrm{2}^{\mathrm{3}^{\mathrm{1}} } +\mathrm{3}^{\mathrm{3}^{\mathrm{1}} } =\mathrm{8}+\mathrm{27}=\mathrm{35}\:\mathrm{mod}\:\mathrm{7}=\mathrm{0} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{1}. \\ $$$$ \\ $$$$\mathrm{let}'\mathrm{s}\:\mathrm{assume}\:\mathrm{it}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n},\:\mathrm{i}.\mathrm{e}. \\ $$$$\mathrm{2}^{\mathrm{3}^{\mathrm{n}} } +\mathrm{3}^{\mathrm{3}^{\mathrm{n}} } \:\mathrm{mod}\:\mathrm{7}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{n}+\mathrm{1}: \\ $$$$\left(\mathrm{2}^{\mathrm{3}^{\mathrm{n}+\mathrm{1}} } +\mathrm{3}^{\mathrm{3}^{\mathrm{n}+\mathrm{1}} } \:\right)\:\mathrm{mod}\:\mathrm{7} \\ $$$$=\left(\mathrm{2}^{\mathrm{3}×\mathrm{3}^{\mathrm{n}} } +\mathrm{3}^{\mathrm{3}×\mathrm{3}^{\mathrm{n}} } \:\right)\:\mathrm{mod}\:\mathrm{7} \\ $$$$=\left[\left(\mathrm{2}^{\mathrm{3}^{\mathrm{n}} } \right)^{\mathrm{3}} +\left(\mathrm{3}^{\mathrm{3}^{\mathrm{n}} } \right)^{\mathrm{3}} \:\right]\:\mathrm{mod}\:\mathrm{7} \\ $$$$=\left[\left(\mathrm{2}^{\mathrm{3}^{\mathrm{n}} } \right)+\left(\mathrm{3}^{\mathrm{3}^{\mathrm{n}} } \right)\right]\left[\left(\mathrm{2}^{\mathrm{3}^{\mathrm{n}} } \right)^{\mathrm{2}} −\left(\mathrm{2}^{\mathrm{3}^{\mathrm{n}} } \right)\left(\mathrm{3}^{\mathrm{3}^{\mathrm{n}} } \right)+\left(\mathrm{3}^{\mathrm{3}^{\mathrm{n}} } \right)^{\mathrm{2}} \right]\:\:\mathrm{mod}\:\mathrm{7} \\ $$$$=\left[\left(\mathrm{2}^{\mathrm{3}^{\mathrm{n}} } \right)+\left(\mathrm{3}^{\mathrm{3}^{\mathrm{n}} } \right)\right]\:\mathrm{mod}\:\mathrm{7} \\ $$$$=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3}^{\mathrm{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$

Commented by hi147 last updated on 04/Oct/17

thx but how u think in 3^(n ) exactly? the prove is not complete... it seems that we must not use congruence methode because this exercise is under the title(divisibility) in secondary book.so we must just use (n divise x ⇔x=kn/k∈Z)... i wait for an other answer ...

$${thx} \\ $$$${but}\:{how}\:{u}\:{think}\:{in}\:\mathrm{3}^{{n}\:} {exactly}?\: \\ $$$${the}\:{prove}\:{is}\:{not}\:{complete}... \\ $$$${it}\:{seems}\:{that}\:{we}\:{must}\:{not}\:{use}\: \\ $$$${congruence}\:{methode}\:{because}\:{this}\: \\ $$$${exercise}\:{is}\:{under}\:{the}\:{title}\left({divisibility}\right) \\ $$$${in}\:{secondary}\:{book}.{so}\:{we}\:{must}\:{just} \\ $$$${use}\:\left({n}\:{divise}\:{x}\:\Leftrightarrow{x}={kn}/{k}\in{Z}\right)... \\ $$$$\:{i}\:{wait}\:{for}\:{an}\:{other}\:{answer}\:... \\ $$

Commented by hi147 last updated on 04/Oct/17

the question is from where come 3^n ? i mean before using the demonstration with concurrence....if we say from imagination.it is not a prove.and as you say.maybe we have other x.so we still need a complet solution...thx

$${the}\:{question}\:{is}\:{from}\:{where}\:{come}\:\mathrm{3}^{{n}} ? \\ $$$${i}\:{mean}\:{before}\:{using}\:{the}\:{demonstration} \\ $$$${with}\:{concurrence}....{if}\:{we}\:{say}\:{from} \\ $$$${imagination}.{it}\:{is}\:{not}\:{a}\:{prove}.{and}\:{as}\: \\ $$$${you}\:{say}.{maybe}\:{we}\:{have}\:{other}\:{x}.{so} \\ $$$${we}\:{still}\:{need}\:{a}\:{complet}\:{solution}...{thx}\: \\ $$$$ \\ $$

Commented by mrW1 last updated on 04/Oct/17

with x=3^n we have proved that 7 divides 2^x +3^x . this prove is complete. but indeed it is not proved that no other solution than 3^n exists.

$$\mathrm{with}\:\mathrm{x}=\mathrm{3}^{\mathrm{n}} \:\mathrm{we}\:\mathrm{have}\:\mathrm{proved}\:\mathrm{that} \\ $$$$\mathrm{7}\:\mathrm{divides}\:\mathrm{2}^{\mathrm{x}} +\mathrm{3}^{\mathrm{x}} . \\ $$$$\mathrm{this}\:\mathrm{prove}\:\mathrm{is}\:\mathrm{complete}. \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{indeed}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{proved}\:\mathrm{that}\:\mathrm{no} \\ $$$$\mathrm{other}\:\mathrm{solution}\:\mathrm{than}\:\mathrm{3}^{\mathrm{n}} \:\mathrm{exists}. \\ $$

Commented by mrW1 last updated on 05/Oct/17

by try and error we get a solution x=3. since a^3 +b^3 =(a+b)(a^2 −ab+b^2 ) we know that x=3×3 is then also a solution, and x=3×3×3 is also a solution, etc. that means x=3^n is a solution.

$$\mathrm{by}\:\mathrm{try}\:\mathrm{and}\:\mathrm{error}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{x}=\mathrm{3}. \\ $$$$\mathrm{since}\:\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right)\:\mathrm{we} \\ $$$$\mathrm{know}\:\mathrm{that}\:\mathrm{x}=\mathrm{3}×\mathrm{3}\:\mathrm{is}\:\mathrm{then}\:\mathrm{also}\:\mathrm{a} \\ $$$$\mathrm{solution},\:\mathrm{and}\:\mathrm{x}=\mathrm{3}×\mathrm{3}×\mathrm{3}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a} \\ $$$$\mathrm{solution},\:\mathrm{etc}.\:\mathrm{that}\:\mathrm{means}\:\mathrm{x}=\mathrm{3}^{\mathrm{n}} \:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{solution}. \\ $$

Commented by mrW1 last updated on 05/Oct/17

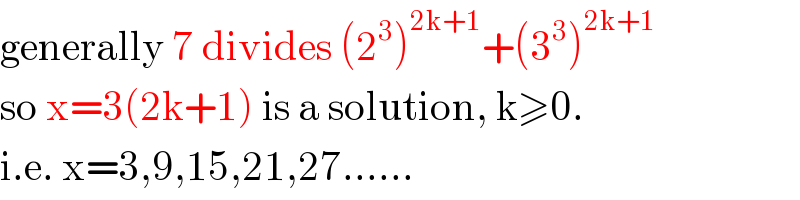
generally 7 divides (2^3 )^(2k+1) +(3^3 )^(2k+1) so x=3(2k+1) is a solution, k≥0. i.e. x=3,9,15,21,27......

$$\mathrm{generally}\:\mathrm{7}\:\mathrm{divides}\:\left(\mathrm{2}^{\mathrm{3}} \right)^{\mathrm{2k}+\mathrm{1}} +\left(\mathrm{3}^{\mathrm{3}} \right)^{\mathrm{2k}+\mathrm{1}} \\ $$$$\mathrm{so}\:\mathrm{x}=\mathrm{3}\left(\mathrm{2k}+\mathrm{1}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution},\:\mathrm{k}\geqslant\mathrm{0}. \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{x}=\mathrm{3},\mathrm{9},\mathrm{15},\mathrm{21},\mathrm{27}...... \\ $$

Commented by hi147 last updated on 06/Oct/17

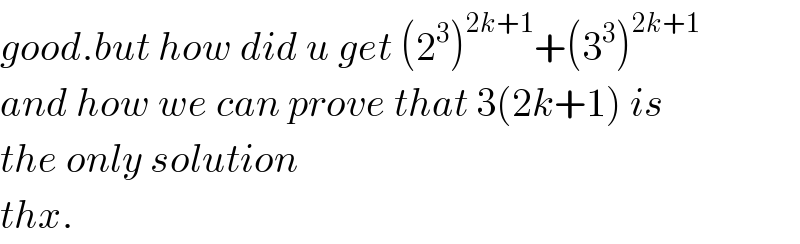
good.but how did u get (2^3 )^(2k+1) +(3^3 )^(2k+1) and how we can prove that 3(2k+1) is the only solution thx.

$${good}.{but}\:{how}\:{did}\:{u}\:{get}\:\left(\mathrm{2}^{\mathrm{3}} \right)^{\mathrm{2}{k}+\mathrm{1}} +\left(\mathrm{3}^{\mathrm{3}} \right)^{\mathrm{2}{k}+\mathrm{1}} \\ $$$${and}\:{how}\:{we}\:{can}\:{prove}\:{that}\:\mathrm{3}\left(\mathrm{2}{k}+\mathrm{1}\right)\:{is} \\ $$$${the}\:{only}\:{solution} \\ $$$${thx}. \\ $$

Commented by mrW1 last updated on 06/Oct/17

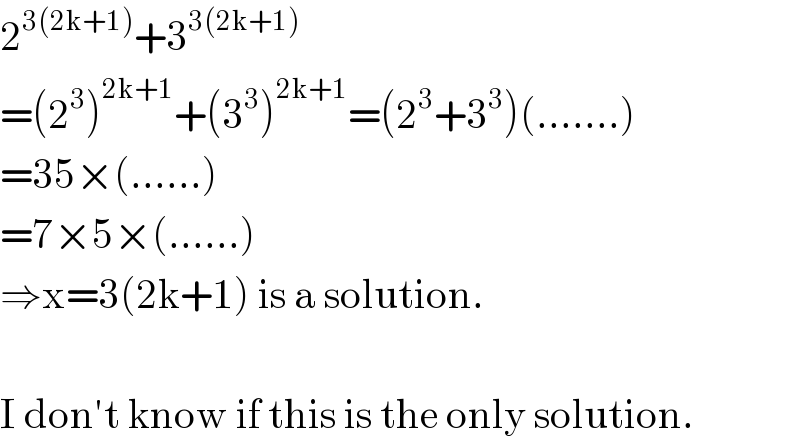
2^(3(2k+1)) +3^(3(2k+1)) =(2^3 )^(2k+1) +(3^3 )^(2k+1) =(2^3 +3^3 )(.......) =35×(......) =7×5×(......) ⇒x=3(2k+1) is a solution. I don′t know if this is the only solution.

$$\mathrm{2}^{\mathrm{3}\left(\mathrm{2k}+\mathrm{1}\right)} +\mathrm{3}^{\mathrm{3}\left(\mathrm{2k}+\mathrm{1}\right)} \\ $$$$=\left(\mathrm{2}^{\mathrm{3}} \right)^{\mathrm{2k}+\mathrm{1}} +\left(\mathrm{3}^{\mathrm{3}} \right)^{\mathrm{2k}+\mathrm{1}} =\left(\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} \right)\left(.......\right) \\ $$$$=\mathrm{35}×\left(......\right) \\ $$$$=\mathrm{7}×\mathrm{5}×\left(......\right) \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3}\left(\mathrm{2k}+\mathrm{1}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com