
Question Number 21874 by tawa tawa last updated on 05/Oct/17

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{if}\:\:\:\mathrm{2}^{\mathrm{2006}} \:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\:\mathrm{17} \\ $$
Answered by mrW1 last updated on 06/Oct/17
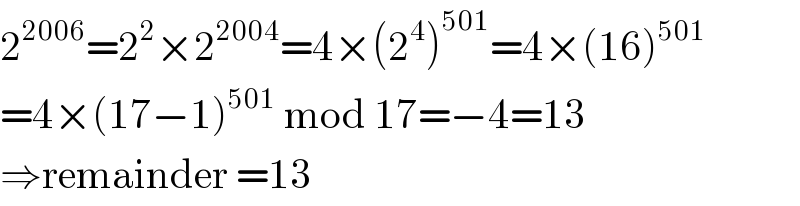
$$\mathrm{2}^{\mathrm{2006}} =\mathrm{2}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2004}} =\mathrm{4}×\left(\mathrm{2}^{\mathrm{4}} \right)^{\mathrm{501}} =\mathrm{4}×\left(\mathrm{16}\right)^{\mathrm{501}} \\ $$$$=\mathrm{4}×\left(\mathrm{17}−\mathrm{1}\right)^{\mathrm{501}} \:\mathrm{mod}\:\mathrm{17}=−\mathrm{4}=\mathrm{13} \\ $$$$\Rightarrow\mathrm{remainder}\:=\mathrm{13} \\ $$
Commented by tawa tawa last updated on 06/Oct/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Tinkutara last updated on 06/Oct/17

$$\mathrm{By}\:\mathrm{Fermat}'\mathrm{s}\:\mathrm{theorem}, \\ $$$$\mathrm{2}^{\mathrm{17}−\mathrm{1}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{17}\right) \\ $$$$\mathrm{2}^{\mathrm{16}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{17}\right) \\ $$$$\mathrm{2}^{\mathrm{2000}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{17}\right) \\ $$$$\mathrm{2}^{\mathrm{2006}} \equiv\mathrm{64}\left(\mathrm{mod}\:\mathrm{17}\right)\equiv\mathrm{13}\left(\mathrm{mod}\:\mathrm{17}\right) \\ $$
Commented by tawa tawa last updated on 06/Oct/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
