
Question and Answers Forum
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 21933 by Tinkutara last updated on 07/Oct/17
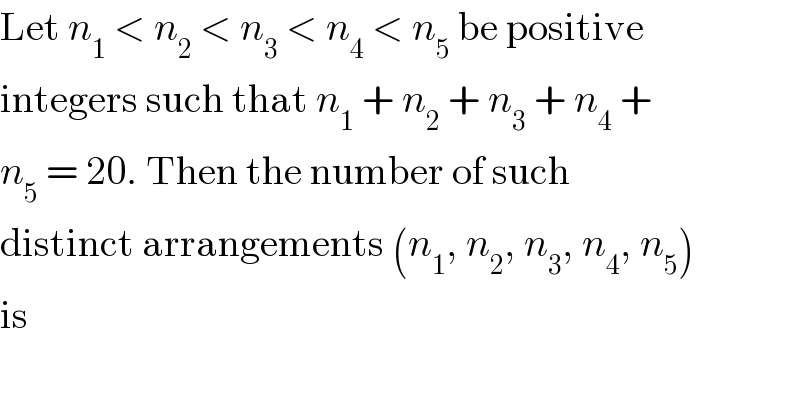
Commented bymrW1 last updated on 08/Oct/17

Commented byRasheed.Sindhi last updated on 08/Oct/17

Commented byRasheed.Sindhi last updated on 08/Oct/17
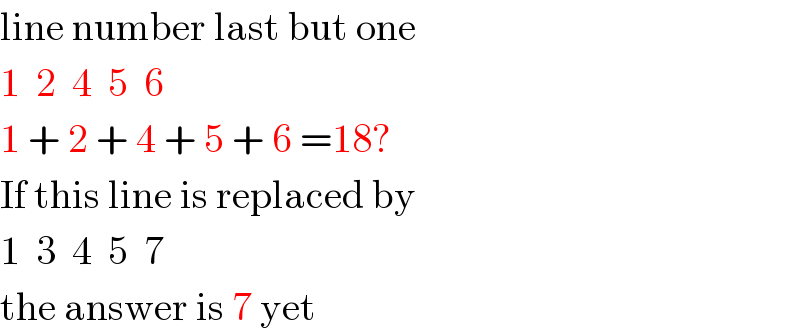
Commented byTinkutara last updated on 08/Oct/17

Commented bymrW1 last updated on 08/Oct/17
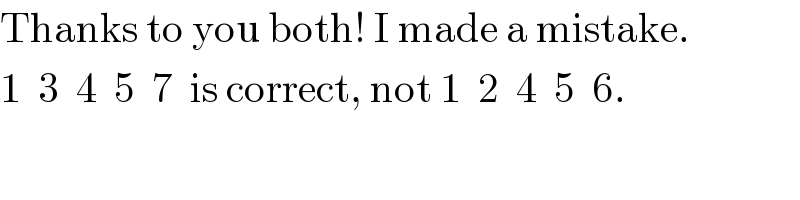
Commented bymrW1 last updated on 09/Oct/17

Commented byTinkutara last updated on 08/Oct/17

Commented bymrW1 last updated on 09/Oct/17

Commented byTinkutara last updated on 09/Oct/17

Commented bymrW1 last updated on 09/Oct/17

Commented bymrW1 last updated on 09/Oct/17

