
Question Number 21940 by Tinkutara last updated on 07/Oct/17
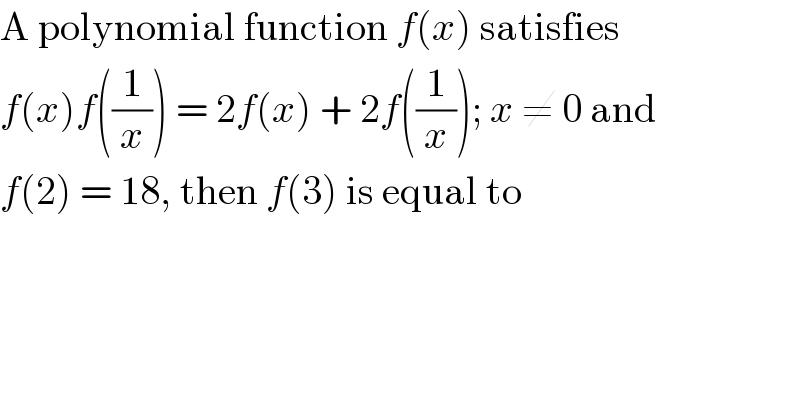
$$\mathrm{A}\:\mathrm{polynomial}\:\mathrm{function}\:{f}\left({x}\right)\:\mathrm{satisfies} \\ $$$${f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\mathrm{2}{f}\left({x}\right)\:+\:\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right);\:{x}\:\neq\:\mathrm{0}\:\mathrm{and} \\ $$$${f}\left(\mathrm{2}\right)\:=\:\mathrm{18},\:\mathrm{then}\:{f}\left(\mathrm{3}\right)\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$
Commented by ajfour last updated on 07/Nov/18
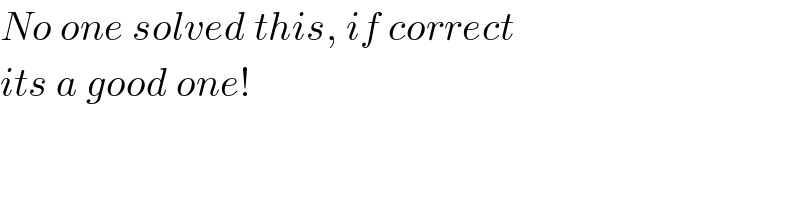
$${No}\:{one}\:{solved}\:{this},\:{if}\:{correct} \\ $$$${its}\:{a}\:{good}\:{one}! \\ $$
Answered by rahul 19 last updated on 08/Nov/18
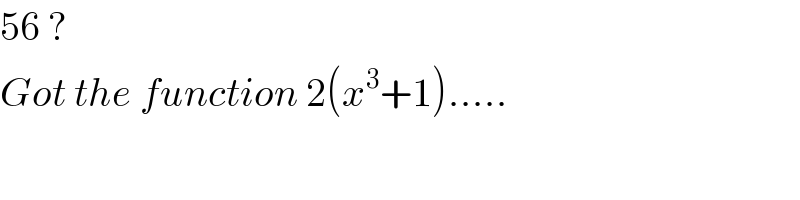
$$\mathrm{56}\:? \\ $$$${Got}\:{the}\:{function}\:\mathrm{2}\left({x}^{\mathrm{3}} +\mathrm{1}\right)..... \\ $$
Commented by ajfour last updated on 08/Nov/18
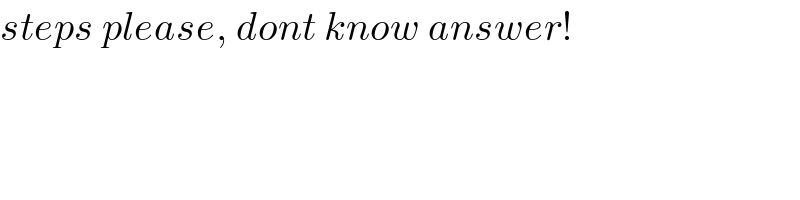
$${steps}\:{please},\:{dont}\:{know}\:{answer}! \\ $$
Answered by rahul 19 last updated on 08/Nov/18
![Let f(x)= a_0 x^n +a_1 x^(n−1) +....+a_(n−1) x+a_n . Acc . to given condition, (a_0 x^n +a_1 x^(n−1) ......+a_n )((a_0 /x^n )+(a_1 /x^(n−1) )+......a_n ) = 2[(a_0 x^n +a_1 x^(n−1) ....+a_n ) + ((a_0 /x^(n ) ) +(a_1 /x^(n−1) )....+a_n )] ⇒ On comparing coeff. of x^n , a_0 a_n = 2a_(0 ) ⇒ a_n =2 On comparing coeff. of x^(n−1) , a_(n−1) =0..... ........similarly,a_(n−2) =.....=a_1 =0 and a_0 = ∓2. ∴ f(x) = 2(∓x^n +1). Now in this case f(2)=18 ⇒ f(x)= 2(x^3 +1) ⇒ f(3)=56.](Q47313.png)
$${Let}\:{f}\left({x}\right)=\:{a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} +....+{a}_{{n}−\mathrm{1}} {x}+{a}_{{n}} . \\ $$$${Acc}\:.\:{to}\:{given}\:{condition}, \\ $$$$\left({a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} ......+{a}_{{n}} \right)\left(\frac{{a}_{\mathrm{0}} }{{x}^{{n}} }+\frac{{a}_{\mathrm{1}} }{{x}^{{n}−\mathrm{1}} }+......{a}_{{n}} \right) \\ $$$$\:=\:\mathrm{2}\left[\left({a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} ....+{a}_{{n}} \right)\:+\:\left(\frac{{a}_{\mathrm{0}} }{{x}^{{n}\:} }\:+\frac{{a}_{\mathrm{1}} }{{x}^{{n}−\mathrm{1}} }....+{a}_{{n}} \right)\right] \\ $$$$\Rightarrow\:{On}\:{comparing}\:{coeff}.\:{of}\:{x}^{{n}} , \\ $$$${a}_{\mathrm{0}} {a}_{{n}} =\:\mathrm{2}{a}_{\mathrm{0}\:} \Rightarrow\:{a}_{{n}} =\mathrm{2} \\ $$$${On}\:{comparing}\:{coeff}.\:{of}\:{x}^{{n}−\mathrm{1}} , \\ $$$${a}_{{n}−\mathrm{1}} =\mathrm{0}..... \\ $$$$........{similarly},{a}_{{n}−\mathrm{2}} =.....={a}_{\mathrm{1}} =\mathrm{0} \\ $$$${and}\:{a}_{\mathrm{0}} =\:\mp\mathrm{2}. \\ $$$$\therefore\:{f}\left({x}\right)\:=\:\mathrm{2}\left(\mp{x}^{{n}} +\mathrm{1}\right). \\ $$$${Now}\:{in}\:{this}\:{case}\: \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{18}\: \\ $$$$\Rightarrow\:{f}\left({x}\right)=\:\mathrm{2}\left({x}^{\mathrm{3}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:{f}\left(\mathrm{3}\right)=\mathrm{56}. \\ $$
Commented by ajfour last updated on 08/Nov/18
$${Yes}\:{Rahul}\:{Sir},\:{Thanks}. \\ $$
Answered by ajfour last updated on 08/Nov/18
![(a_n x^n +a_(n−1) x^(n−1) +...+a_1 x+a_0 ) ×(1/x^n )(a_n +a_(n−1) x+....+a_1 x^(n−1) +a_0 x^n ) = (1/x^n )[a_n a_0 x^(2n) +(a_(n−1) a_0 +a_n a_1 )x^(2n−1) +.... .....+(a_n a_n +a_(n−1) a_(n−1) +...+a_0 a_0 +)x^n +... ...+(a_1 a_n +a_0 a_(n−1) )x+a_0 a_n ] = (2/x^n )[(a_n x^(2n) +a_(n−1) x^(2n−1) +.... ....+a_0 x^n )+(a_0 x^n +a_1 x^(n−1) +... ....+a_(n−1) x+a_n )] comparing coeffs. a_n a_0 = 2a_n ⇒ a_0 = 2 a_(n−1) a_0 +a_n a_1 = 2a_(n−1) ⇒ a_1 =0 a_n a_2 +a_(n−1) a_1 +a_(n−2) a_0 = 2a_(n−2) ⇒ a_2 = 0 and so on.. So f(x)= a_n x^n +2 f(1)×f(1)=4f(1) ⇒ f(1)= 0, 4 ⇒ a_n +2 = 0, 4 ⇒ a_n = ±2 ⇒ f(2)=±2(2^n +1) = 18 So a_n = 2 & n= 3 f(3)= 2(3^3 +1)= 56 .](Q47323.png)
$$\left({a}_{{n}} {x}^{{n}} +{a}_{{n}−\mathrm{1}} {x}^{{n}−\mathrm{1}} +...+{a}_{\mathrm{1}} {x}+{a}_{\mathrm{0}} \right) \\ $$$$×\frac{\mathrm{1}}{{x}^{{n}} }\left({a}_{{n}} +{a}_{{n}−\mathrm{1}} {x}+....+{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} +{a}_{\mathrm{0}} {x}^{{n}} \right) \\ $$$$\:=\:\frac{\mathrm{1}}{{x}^{{n}} }\left[{a}_{{n}} {a}_{\mathrm{0}} {x}^{\mathrm{2}{n}} +\left({a}_{{n}−\mathrm{1}} {a}_{\mathrm{0}} +{a}_{{n}} {a}_{\mathrm{1}} \right){x}^{\mathrm{2}{n}−\mathrm{1}} +....\right. \\ $$$$\:\:.....+\left({a}_{{n}} {a}_{{n}} +{a}_{{n}−\mathrm{1}} {a}_{{n}−\mathrm{1}} +...+{a}_{\mathrm{0}} {a}_{\mathrm{0}} +\right){x}^{{n}} \:+... \\ $$$$\left....+\left({a}_{\mathrm{1}} {a}_{{n}} +{a}_{\mathrm{0}} {a}_{{n}−\mathrm{1}} \right){x}+{a}_{\mathrm{0}} {a}_{{n}} \:\right] \\ $$$$\:\:=\:\frac{\mathrm{2}}{{x}^{{n}} }\left[\left({a}_{{n}} {x}^{\mathrm{2}{n}} +{a}_{{n}−\mathrm{1}} {x}^{\mathrm{2}{n}−\mathrm{1}} +....\right.\right. \\ $$$$\left.\:\:\:\:\:\:....+{a}_{\mathrm{0}} {x}^{{n}} \right)+\left({a}_{\mathrm{0}} {x}^{{n}} +{a}_{\mathrm{1}} {x}^{{n}−\mathrm{1}} +...\right. \\ $$$$\left.\:\left.\:\:\:\:\:\:....+{a}_{{n}−\mathrm{1}} {x}+{a}_{{n}} \right)\right] \\ $$$${comparing}\:{coeffs}. \\ $$$$\:\:\:\:{a}_{{n}} {a}_{\mathrm{0}} \:=\:\mathrm{2}{a}_{{n}} \:\:\:\:\Rightarrow\:\:{a}_{\mathrm{0}} =\:\mathrm{2} \\ $$$$\:\:\:\:{a}_{{n}−\mathrm{1}} {a}_{\mathrm{0}} +{a}_{{n}} {a}_{\mathrm{1}} =\:\mathrm{2}{a}_{{n}−\mathrm{1}} \:\:\Rightarrow\:{a}_{\mathrm{1}} =\mathrm{0} \\ $$$$\:\:\:\:{a}_{{n}} {a}_{\mathrm{2}} +{a}_{{n}−\mathrm{1}} {a}_{\mathrm{1}} +{a}_{{n}−\mathrm{2}} {a}_{\mathrm{0}} =\:\mathrm{2}{a}_{{n}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:{a}_{\mathrm{2}} =\:\mathrm{0} \\ $$$${and}\:{so}\:{on}.. \\ $$$${So}\:\:{f}\left({x}\right)=\:{a}_{{n}} {x}^{{n}} +\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:{f}\left(\mathrm{1}\right)×{f}\left(\mathrm{1}\right)=\mathrm{4}{f}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\:\:{f}\left(\mathrm{1}\right)=\:\mathrm{0},\:\mathrm{4} \\ $$$$\Rightarrow\:\:\:\:\:\:{a}_{{n}} +\mathrm{2}\:=\:\mathrm{0},\:\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:{a}_{{n}} =\:\pm\mathrm{2} \\ $$$$\Rightarrow\:\:\:{f}\left(\mathrm{2}\right)=\pm\mathrm{2}\left(\mathrm{2}^{{n}} +\mathrm{1}\right)\:=\:\mathrm{18} \\ $$$${So}\:\:\:{a}_{{n}} =\:\mathrm{2}\:\:\&\:\:{n}=\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:{f}\left(\mathrm{3}\right)=\:\mathrm{2}\left(\mathrm{3}^{\mathrm{3}} +\mathrm{1}\right)=\:\mathrm{56}\:. \\ $$$$ \\ $$
