Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 170794 by mr W last updated on 30/May/22

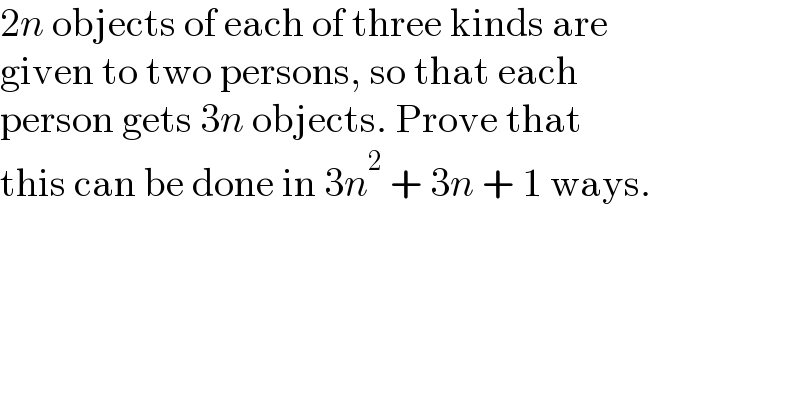
2n objects of each of three kinds are given to two persons, so that each person gets 3n objects. Prove that this can be done in 3n^2 + 3n + 1 ways.

$$\mathrm{2}{n}\:\mathrm{objects}\:\mathrm{of}\:\mathrm{each}\:\mathrm{of}\:\mathrm{three}\:\mathrm{kinds}\:\mathrm{are} \\ $$$$\mathrm{given}\:\mathrm{to}\:\mathrm{two}\:\mathrm{persons},\:\mathrm{so}\:\mathrm{that}\:\mathrm{each} \\ $$$$\mathrm{person}\:\mathrm{gets}\:\mathrm{3}{n}\:\mathrm{objects}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{done}\:\mathrm{in}\:\mathrm{3}{n}^{\mathrm{2}} \:+\:\mathrm{3}{n}\:+\:\mathrm{1}\:\mathrm{ways}. \\ $$

Answered by aleks041103 last updated on 05/Jun/22

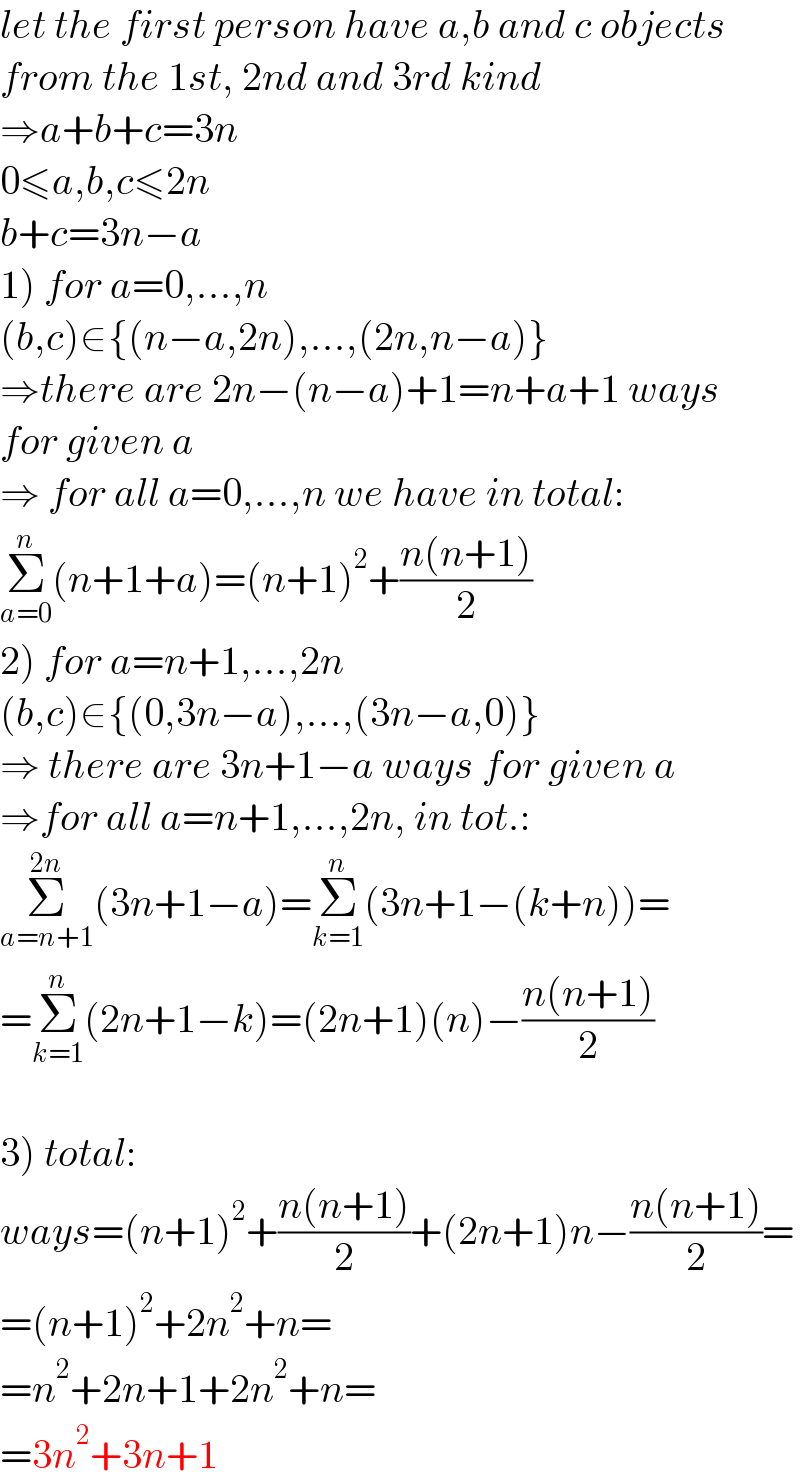
let the first person have a,b and c objects from the 1st, 2nd and 3rd kind ⇒a+b+c=3n 0≤a,b,c≤2n b+c=3n−a 1) for a=0,...,n (b,c)∈{(n−a,2n),...,(2n,n−a)} ⇒there are 2n−(n−a)+1=n+a+1 ways for given a ⇒ for all a=0,...,n we have in total: Σ_(a=0) ^n (n+1+a)=(n+1)^2 +((n(n+1))/2) 2) for a=n+1,...,2n (b,c)∈{(0,3n−a),...,(3n−a,0)} ⇒ there are 3n+1−a ways for given a ⇒for all a=n+1,...,2n, in tot.: Σ_(a=n+1) ^(2n) (3n+1−a)=Σ_(k=1) ^n (3n+1−(k+n))= =Σ_(k=1) ^n (2n+1−k)=(2n+1)(n)−((n(n+1))/2) 3) total: ways=(n+1)^2 +((n(n+1))/2)+(2n+1)n−((n(n+1))/2)= =(n+1)^2 +2n^2 +n= =n^2 +2n+1+2n^2 +n= =3n^2 +3n+1

$${let}\:{the}\:{first}\:{person}\:{have}\:{a},{b}\:{and}\:{c}\:{objects} \\ $$$${from}\:{the}\:\mathrm{1}{st},\:\mathrm{2}{nd}\:{and}\:\mathrm{3}{rd}\:{kind} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{3}{n} \\ $$$$\mathrm{0}\leqslant{a},{b},{c}\leqslant\mathrm{2}{n} \\ $$$${b}+{c}=\mathrm{3}{n}−{a} \\ $$$$\left.\mathrm{1}\right)\:{for}\:{a}=\mathrm{0},...,{n} \\ $$$$\left({b},{c}\right)\in\left\{\left({n}−{a},\mathrm{2}{n}\right),...,\left(\mathrm{2}{n},{n}−{a}\right)\right\} \\ $$$$\Rightarrow{there}\:{are}\:\mathrm{2}{n}−\left({n}−{a}\right)+\mathrm{1}={n}+{a}+\mathrm{1}\:{ways} \\ $$$${for}\:{given}\:{a} \\ $$$$\Rightarrow\:{for}\:{all}\:{a}=\mathrm{0},...,{n}\:{we}\:{have}\:{in}\:{total}: \\ $$$$\underset{{a}=\mathrm{0}} {\overset{{n}} {\sum}}\left({n}+\mathrm{1}+{a}\right)=\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:{for}\:{a}={n}+\mathrm{1},...,\mathrm{2}{n} \\ $$$$\left({b},{c}\right)\in\left\{\left(\mathrm{0},\mathrm{3}{n}−{a}\right),...,\left(\mathrm{3}{n}−{a},\mathrm{0}\right)\right\} \\ $$$$\Rightarrow\:{there}\:{are}\:\mathrm{3}{n}+\mathrm{1}−{a}\:{ways}\:{for}\:{given}\:{a} \\ $$$$\Rightarrow{for}\:{all}\:{a}={n}+\mathrm{1},...,\mathrm{2}{n},\:{in}\:{tot}.: \\ $$$$\underset{{a}={n}+\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\left(\mathrm{3}{n}+\mathrm{1}−{a}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}{n}+\mathrm{1}−\left({k}+{n}\right)\right)= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}{n}+\mathrm{1}−{k}\right)=\left(\mathrm{2}{n}+\mathrm{1}\right)\left({n}\right)−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$ \\ $$$$\left.\mathrm{3}\right)\:{total}: \\ $$$${ways}=\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}+\left(\mathrm{2}{n}+\mathrm{1}\right){n}−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}= \\ $$$$=\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{n}^{\mathrm{2}} +{n}= \\ $$$$={n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}+\mathrm{2}{n}^{\mathrm{2}} +{n}= \\ $$$$=\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{1} \\ $$

Commented by mr W last updated on 05/Jun/22

thanks sir!

$${thanks}\:{sir}! \\ $$

Answered by mr W last updated on 06/Jun/22

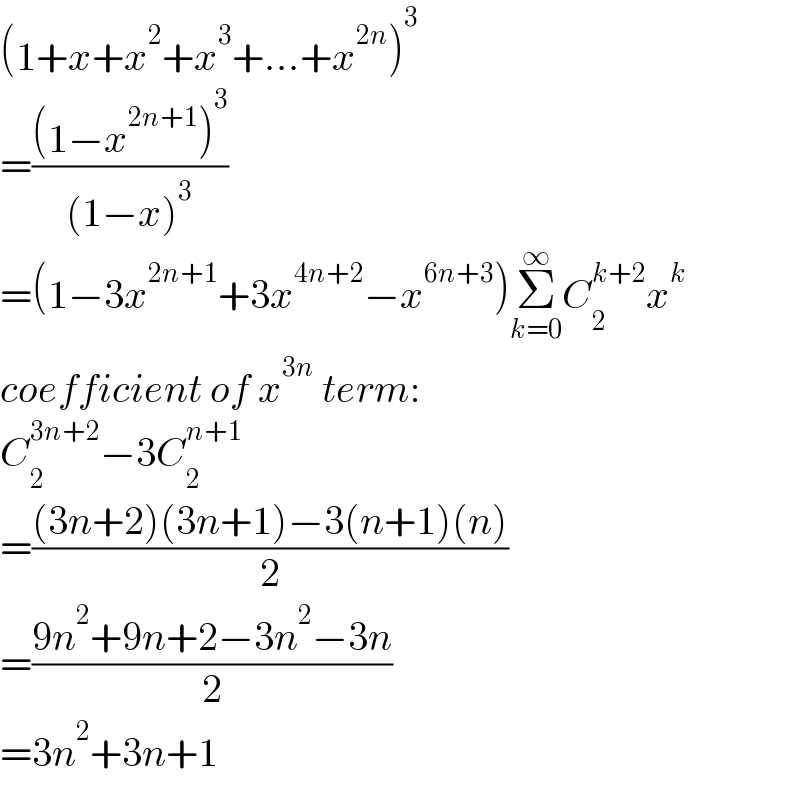
(1+x+x^2 +x^3 +...+x^(2n) )^3 =(((1−x^(2n+1) )^3 )/((1−x)^3 )) =(1−3x^(2n+1) +3x^(4n+2) −x^(6n+3) )Σ_(k=0) ^∞ C_2 ^(k+2) x^k coefficient of x^(3n) term: C_2 ^(3n+2) −3C_2 ^(n+1) =(((3n+2)(3n+1)−3(n+1)(n))/2) =((9n^2 +9n+2−3n^2 −3n)/2) =3n^2 +3n+1

$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...+{x}^{\mathrm{2}{n}} \right)^{\mathrm{3}} \\ $$$$=\frac{\left(\mathrm{1}−{x}^{\mathrm{2}{n}+\mathrm{1}} \right)^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$=\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{3}{x}^{\mathrm{4}{n}+\mathrm{2}} −{x}^{\mathrm{6}{n}+\mathrm{3}} \right)\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {x}^{{k}} \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{3}{n}} \:{term}: \\ $$$${C}_{\mathrm{2}} ^{\mathrm{3}{n}+\mathrm{2}} −\mathrm{3}{C}_{\mathrm{2}} ^{{n}+\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)−\mathrm{3}\left({n}+\mathrm{1}\right)\left({n}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{9}{n}^{\mathrm{2}} +\mathrm{9}{n}+\mathrm{2}−\mathrm{3}{n}^{\mathrm{2}} −\mathrm{3}{n}}{\mathrm{2}} \\ $$$$=\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{1} \\ $$

Commented by aleks041103 last updated on 05/Jun/22

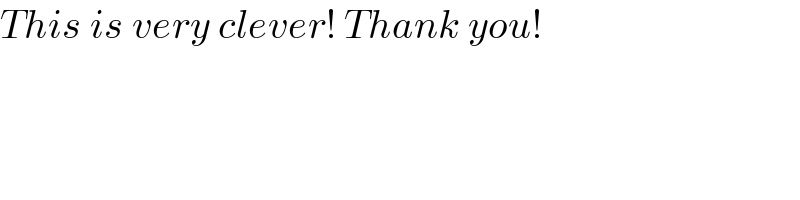
This is very clever! Thank you!

$${This}\:{is}\:{very}\:{clever}!\:{Thank}\:{you}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com