
Question and Answers Forum
Question Number 22116 by ajfour last updated on 11/Oct/17

Commented by ajfour last updated on 11/Oct/17
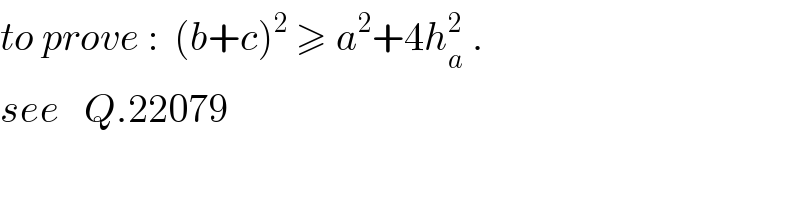
Answered by ajfour last updated on 11/Oct/17
![a^2 =b^2 +c^2 −2bc cos (θ+φ) =(b+c)^2 −2bc[1+cos (θ+φ)] =(b+c)^2 −2bc[1+2cos θcos φ −cos θcos φ −sin θsin φ] =(b+c)^2 −2bc[1+2×(h_a /c).(h_a /b)−cos (θ−φ)] =(b+c)^2 −4h_a ^2 −2bc[1−cos (θ−φ)] so (b+c)^2 −a^2 −4h_a ^2 =4bcsin^2 (((θ−φ)/2))≥0 .](Q22118.png)
Commented by Tinkutara last updated on 11/Oct/17
| ||
Question and Answers Forum | ||
Question Number 22116 by ajfour last updated on 11/Oct/17 | ||
 | ||
Commented by ajfour last updated on 11/Oct/17 | ||
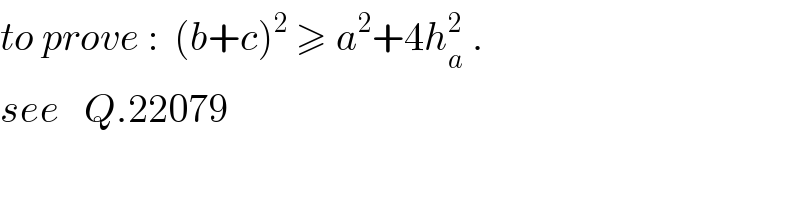 | ||
Answered by ajfour last updated on 11/Oct/17 | ||
![a^2 =b^2 +c^2 −2bc cos (θ+φ) =(b+c)^2 −2bc[1+cos (θ+φ)] =(b+c)^2 −2bc[1+2cos θcos φ −cos θcos φ −sin θsin φ] =(b+c)^2 −2bc[1+2×(h_a /c).(h_a /b)−cos (θ−φ)] =(b+c)^2 −4h_a ^2 −2bc[1−cos (θ−φ)] so (b+c)^2 −a^2 −4h_a ^2 =4bcsin^2 (((θ−φ)/2))≥0 .](Q22118.png) | ||
| ||
Commented by Tinkutara last updated on 11/Oct/17 | ||
 | ||