
Question Number 22304 by Tinkutara last updated on 15/Oct/17

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{along} \\ $$$${x}-\mathrm{axis}.\:\mathrm{At}\:{t}\:=\:\mathrm{0},\:\mathrm{it}\:\mathrm{is}\:\mathrm{released}\:\mathrm{from} \\ $$$$\mathrm{rest}\:\mathrm{at}\:{x}\:=\:{a}.\:\mathrm{Acceleration}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{particle}\:\mathrm{varies}\:\mathrm{as}\:\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }\:=\:−\frac{{k}}{{x}^{\mathrm{2}} }\:,\:\mathrm{where}\:{k} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{constant}. \\ $$$$\mathrm{Time}\:\mathrm{required}\:\mathrm{by}\:\mathrm{particle}\:\mathrm{to}\:\mathrm{reach}\:\mathrm{the} \\ $$$$\mathrm{origin}\:\mathrm{will}\:\mathrm{be} \\ $$
Answered by ajfour last updated on 16/Oct/17
![(d^2 x/dt^2 )=((vdv)/dx)=−(k/x^2 ) ⇒ ∫_0 ^( v) vdv = −∫_a ^( x) ((kdx)/x^2 ) ⇒ (v^2 /2) = +k((1/x)−(1/a)) or v=−(√(2k)) (√((1/x)−(1/a))) ⇒ ∫_a ^( x) (dx/(√((1/x)−(1/a)))) =−(√(2k)) ∫_0 ^( t) dt time taken to reach x=0 be T ⇒ T=(1/(√(2k)))∫_0 ^( a) (√((ax)/(a−x))) dx let a−x=y^2 ⇒ dx=−2ydy x=a−y^2 ; x=0 ⇒ y=(√a) and x=a ⇒ y=0 ; then T=(1/(√(2k)))∫_(√a) ^( 0) ((√(a(a−y^2 )))/y)(−2ydy) =(√((2a)/k))∫_0 ^( (√a)) (√(((√a))^2 −y^2 )) dy =(√((2a)/k)) [(y/2)(√(a−y^2 ))∣_0 ^(√a) +(a/2)sin^(−1) ((y/(√a)))∣_0 ^(√a) ] T=(√((2a)/k)) ((a/2)×(𝛑/2))=((𝛑a)/2)(√(a/(2k))) .](Q22306.png)
$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }=\frac{{vdv}}{{dx}}=−\frac{{k}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\:{v}} {vdv}\:=\:−\int_{{a}} ^{\:\:{x}} \:\frac{{kdx}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{v}^{\mathrm{2}} }{\mathrm{2}}\:=\:+{k}\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{a}}\right) \\ $$$${or}\:\:\:\:\:\:{v}=−\sqrt{\mathrm{2}{k}}\:\sqrt{\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{a}}}\: \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\int_{{a}} ^{\:\:{x}} \frac{{dx}}{\sqrt{\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{a}}}}\:=−\sqrt{\mathrm{2}{k}}\:\int_{\mathrm{0}} ^{\:{t}} {dt} \\ $$$${time}\:{taken}\:{to}\:{reach}\:{x}=\mathrm{0}\:{be}\:{T} \\ $$$$\Rightarrow\:\:\:{T}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}{k}}}\int_{\mathrm{0}} ^{\:\:{a}} \sqrt{\frac{{ax}}{{a}−{x}}}\:{dx} \\ $$$${let}\:\:{a}−{x}={y}^{\mathrm{2}} \:\:\:\:\Rightarrow\:\:{dx}=−\mathrm{2}{ydy} \\ $$$$\:\:\:\:{x}={a}−{y}^{\mathrm{2}} \:\:;\:{x}=\mathrm{0}\:\Rightarrow\:{y}=\sqrt{{a}}\: \\ $$$${and}\:\:{x}={a}\:\Rightarrow\:{y}=\mathrm{0}\:;\:{then} \\ $$$$\:\:\:\:\:\:\:\:{T}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}{k}}}\int_{\sqrt{{a}}} ^{\:\:\mathrm{0}} \frac{\sqrt{{a}\left({a}−{y}^{\mathrm{2}} \right)}}{{y}}\left(−\mathrm{2}{ydy}\right) \\ $$$$\:\:=\sqrt{\frac{\mathrm{2}{a}}{{k}}}\int_{\mathrm{0}} ^{\:\:\sqrt{{a}}} \sqrt{\left(\sqrt{{a}}\right)^{\mathrm{2}} −{y}^{\mathrm{2}} }\:{dy} \\ $$$$\:=\sqrt{\frac{\mathrm{2}{a}}{{k}}}\:\left[\frac{{y}}{\mathrm{2}}\sqrt{{a}−{y}^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\sqrt{{a}}} +\frac{{a}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{{y}}{\sqrt{{a}}}\right)\mid_{\mathrm{0}} ^{\sqrt{{a}}} \right] \\ $$$$\boldsymbol{{T}}=\sqrt{\frac{\mathrm{2}\boldsymbol{{a}}}{\boldsymbol{{k}}}}\:\left(\frac{\boldsymbol{{a}}}{\mathrm{2}}×\frac{\boldsymbol{\pi}}{\mathrm{2}}\right)=\frac{\boldsymbol{\pi{a}}}{\mathrm{2}}\sqrt{\frac{\boldsymbol{{a}}}{\mathrm{2}\boldsymbol{{k}}}}\:. \\ $$
Commented by squidward last updated on 16/Oct/17
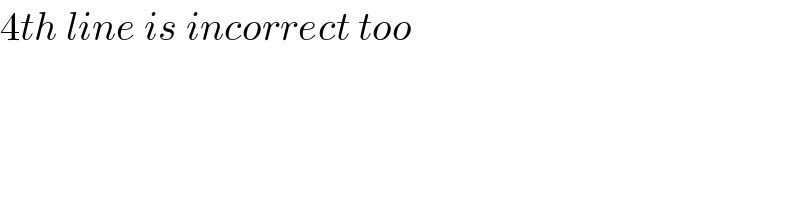
$$\mathrm{4}{th}\:{line}\:{is}\:{incorrect}\:{too} \\ $$
Commented by Tinkutara last updated on 15/Oct/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by squidward last updated on 16/Oct/17

$${your}\:\mathrm{3}{rd}\:{line}\:{is}\:{wrong}\:{and}\:{how}\:{the}\:{hell} \\ $$$${did}\:{you}\:{go}\:{from}\:\mathrm{3}{rd}\:{line}\:{to}\:\mathrm{4}{th}? \\ $$
Commented by ajfour last updated on 16/Oct/17

$${is}\:{it}\:{fine}\:{now}\:? \\ $$
Commented by ajfour last updated on 16/Oct/17

$${No}.\:{after}\:{being}\:{released}\:{at}\:{x}={a} \\ $$$${particle}\:{develops}\:{negative}\:{velocity}. \\ $$$$\:{v}=\pm\sqrt{\mathrm{2}{k}}\:\sqrt{\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{a}}}\: \\ $$$${so}\:{we}\:{choose}\:{the}\:−{ve}\:{one}\:. \\ $$
Commented by Tinkutara last updated on 25/Nov/17
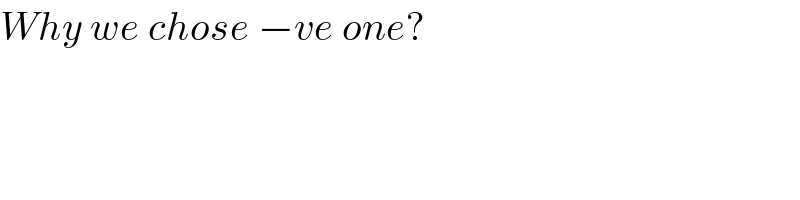
$${Why}\:{we}\:{chose}\:−{ve}\:{one}? \\ $$
