Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 22370 by Tinkutara last updated on 16/Oct/17

A uniform flexible chain of length (3/2) m rests on a fixed smooth sphere of radius R = (2/π) m such that one end A of chain is on the top of the sphere while the other end B is hanging freely. Chain is held stationary by a horizontal thread PA. Calculate the acceleration of chain when the horizontal string PA is burnt. (g = 10 m/s^2 )

$$\mathrm{A}\:\mathrm{uniform}\:\mathrm{flexible}\:\mathrm{chain}\:\mathrm{of}\:\mathrm{length}\:\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{m} \\ $$$$\mathrm{rests}\:\mathrm{on}\:\mathrm{a}\:\mathrm{fixed}\:\mathrm{smooth}\:\mathrm{sphere}\:\mathrm{of} \\ $$$$\mathrm{radius}\:{R}\:=\:\frac{\mathrm{2}}{\pi}\:\mathrm{m}\:\mathrm{such}\:\mathrm{that}\:\mathrm{one}\:\mathrm{end}\:{A}\:\mathrm{of} \\ $$$$\mathrm{chain}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sphere}\:\mathrm{while} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{end}\:{B}\:\mathrm{is}\:\mathrm{hanging}\:\mathrm{freely}.\:\mathrm{Chain} \\ $$$$\mathrm{is}\:\mathrm{held}\:\mathrm{stationary}\:\mathrm{by}\:\mathrm{a}\:\mathrm{horizontal} \\ $$$$\mathrm{thread}\:{PA}.\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{acceleration} \\ $$$$\mathrm{of}\:\mathrm{chain}\:\mathrm{when}\:\mathrm{the}\:\mathrm{horizontal}\:\mathrm{string}\:{PA} \\ $$$$\mathrm{is}\:\mathrm{burnt}.\:\left({g}\:=\:\mathrm{10}\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \right) \\ $$

Commented by mrW1 last updated on 17/Oct/17

AC^(⌢) =((πr)/2)=(π/2)×(2/π)= 1 m BC=(3/2)−1=(1/2) m ρ=mass each meter a=acceleration T_0 =tension at point C, at θ=0 (1/2)ρg−T_0 =(1/2)ρa ⇒T_0 =(1/2)ρ(g−a) −dT+ρgdscos θ=aρds −dT=ρds(a−gcos θ) −dT=ρr(a−gcos θ)dθ −∫_T_0 ^( 0) dT=ρr∫_0 ^(π/2) (a−gcos θ)dθ T_0 =ρr[aθ−gsin θ]_0 ^(π/2) T_0 =ρr[((aπ)/2)−g] (1/2)ρ(g−a)=ρ(2/π)(((aπ)/2)−g) (g−a)=(4/π)(((aπ)/2)−g) g−a=2a−(4/π)g ⇒a=((4+π)/(3π))g ≈ 7.58 m/s^2

$$\overset{\frown} {\mathrm{AC}}=\frac{\pi\mathrm{r}}{\mathrm{2}}=\frac{\pi}{\mathrm{2}}×\frac{\mathrm{2}}{\pi}=\:\mathrm{1}\:\mathrm{m} \\ $$$$\mathrm{BC}=\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{m} \\ $$$$\rho=\mathrm{mass}\:\mathrm{each}\:\mathrm{meter} \\ $$$$\mathrm{a}=\mathrm{acceleration} \\ $$$$\mathrm{T}_{\mathrm{0}} =\mathrm{tension}\:\mathrm{at}\:\mathrm{point}\:\mathrm{C},\:\mathrm{at}\:\theta=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\rho\mathrm{g}−\mathrm{T}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\rho\mathrm{a} \\ $$$$\Rightarrow\mathrm{T}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\rho\left(\mathrm{g}−\mathrm{a}\right) \\ $$$$ \\ $$$$−\mathrm{dT}+\rho\mathrm{gdscos}\:\theta=\mathrm{a}\rho\mathrm{ds} \\ $$$$−\mathrm{dT}=\rho\mathrm{ds}\left(\mathrm{a}−\mathrm{gcos}\:\theta\right) \\ $$$$−\mathrm{dT}=\rho\mathrm{r}\left(\mathrm{a}−\mathrm{gcos}\:\theta\right)\mathrm{d}\theta \\ $$$$−\int_{\mathrm{T}_{\mathrm{0}} } ^{\:\mathrm{0}} \mathrm{dT}=\rho\mathrm{r}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{a}−\mathrm{gcos}\:\theta\right)\mathrm{d}\theta \\ $$$$\mathrm{T}_{\mathrm{0}} =\rho\mathrm{r}\left[\mathrm{a}\theta−\mathrm{gsin}\:\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{T}_{\mathrm{0}} =\rho\mathrm{r}\left[\frac{\mathrm{a}\pi}{\mathrm{2}}−\mathrm{g}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\rho\left(\mathrm{g}−\mathrm{a}\right)=\rho\frac{\mathrm{2}}{\pi}\left(\frac{\mathrm{a}\pi}{\mathrm{2}}−\mathrm{g}\right) \\ $$$$\left(\mathrm{g}−\mathrm{a}\right)=\frac{\mathrm{4}}{\pi}\left(\frac{\mathrm{a}\pi}{\mathrm{2}}−\mathrm{g}\right) \\ $$$$\mathrm{g}−\mathrm{a}=\mathrm{2a}−\frac{\mathrm{4}}{\pi}\mathrm{g} \\ $$$$\Rightarrow\mathrm{a}=\frac{\mathrm{4}+\pi}{\mathrm{3}\pi}\mathrm{g}\:\approx\:\mathrm{7}.\mathrm{58}\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \\ $$

Commented by Tinkutara last updated on 16/Oct/17

Commented by Tinkutara last updated on 17/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by revenge last updated on 18/Oct/17

Commented by revenge last updated on 18/Oct/17

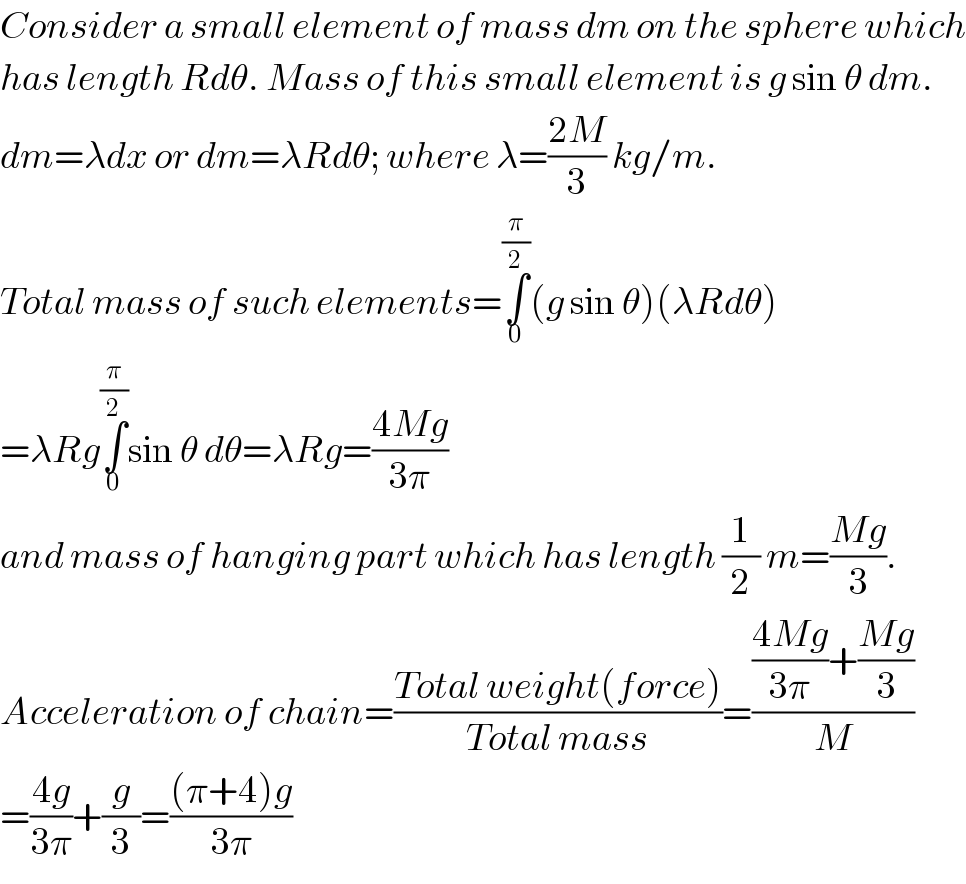
Consider a small element of mass dm on the sphere which has length Rdθ. Mass of this small element is g sin θ dm. dm=λdx or dm=λRdθ; where λ=((2M)/3) kg/m. Total mass of such elements=∫_0 ^(π/2) (g sin θ)(λRdθ) =λRg∫_0 ^(π/2) sin θ dθ=λRg=((4Mg)/(3π)) and mass of hanging part which has length (1/2) m=((Mg)/3). Acceleration of chain=((Total weight(force))/(Total mass))=((((4Mg)/(3π))+((Mg)/3))/M) =((4g)/(3π))+(g/3)=(((π+4)g)/(3π))

$${Consider}\:{a}\:{small}\:{element}\:{of}\:{mass}\:{dm}\:{on}\:{the}\:{sphere}\:{which} \\ $$$${has}\:{length}\:{Rd}\theta.\:{Mass}\:{of}\:{this}\:{small}\:{element}\:{is}\:{g}\:\mathrm{sin}\:\theta\:{dm}. \\ $$$${dm}=\lambda{dx}\:{or}\:{dm}=\lambda{Rd}\theta;\:{where}\:\lambda=\frac{\mathrm{2}{M}}{\mathrm{3}}\:{kg}/{m}. \\ $$$${Total}\:{mass}\:{of}\:{such}\:{elements}=\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\left({g}\:\mathrm{sin}\:\theta\right)\left(\lambda{Rd}\theta\right) \\ $$$$=\lambda{Rg}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\mathrm{sin}\:\theta\:{d}\theta=\lambda{Rg}=\frac{\mathrm{4}{Mg}}{\mathrm{3}\pi} \\ $$$${and}\:{mass}\:{of}\:{hanging}\:{part}\:{which}\:{has}\:{length}\:\frac{\mathrm{1}}{\mathrm{2}}\:{m}=\frac{{Mg}}{\mathrm{3}}. \\ $$$${Acceleration}\:{of}\:{chain}=\frac{{Total}\:{weight}\left({force}\right)}{{Total}\:{mass}}=\frac{\frac{\mathrm{4}{Mg}}{\mathrm{3}\pi}+\frac{{Mg}}{\mathrm{3}}}{{M}} \\ $$$$=\frac{\mathrm{4}{g}}{\mathrm{3}\pi}+\frac{{g}}{\mathrm{3}}=\frac{\left(\pi+\mathrm{4}\right){g}}{\mathrm{3}\pi} \\ $$

Commented by Tinkutara last updated on 18/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com