Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 22518 by ajfour last updated on 19/Oct/17

Commented by ajfour last updated on 19/Oct/17

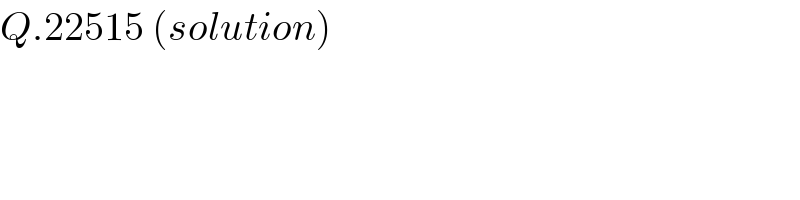
Q.22515 (solution)

$${Q}.\mathrm{22515}\:\left({solution}\right) \\ $$

Answered by ajfour last updated on 19/Oct/17

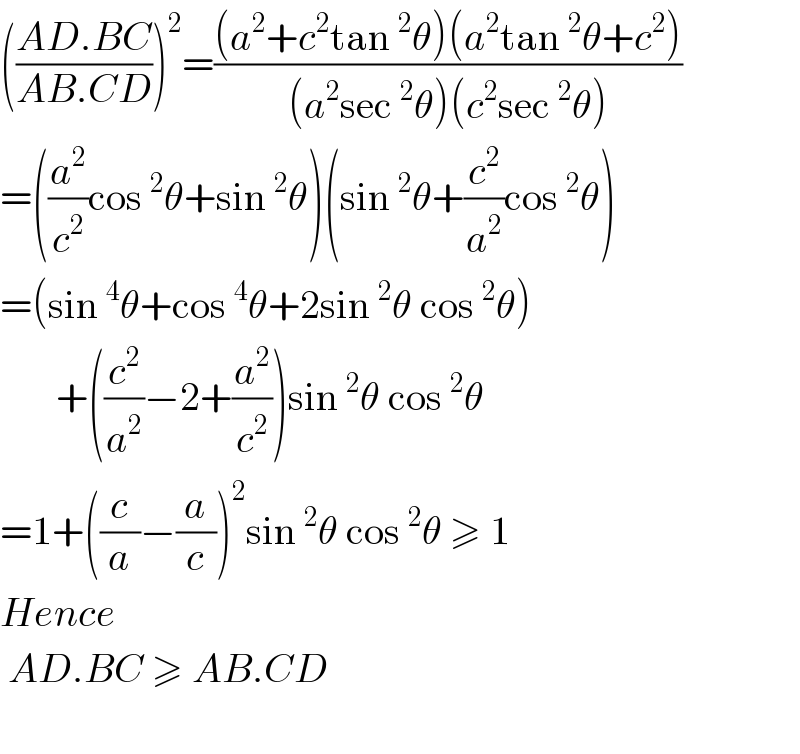
(((AD.BC)/(AB.CD)))^2 =(((a^2 +c^2 tan^2 θ)(a^2 tan^2 θ+c^2 ))/((a^2 sec^2 θ)(c^2 sec^2 θ))) =((a^2 /c^2 )cos^2 θ+sin^2 θ)(sin^2 θ+(c^2 /a^2 )cos^2 θ) =(sin^4 θ+cos^4 θ+2sin^2 θ cos^2 θ) +((c^2 /a^2 )−2+(a^2 /c^2 ))sin^2 θ cos^2 θ =1+((c/a)−(a/c))^2 sin^2 θ cos^2 θ ≥ 1 Hence AD.BC ≥ AB.CD

$$\left(\frac{{AD}.{BC}}{{AB}.{CD}}\right)^{\mathrm{2}} =\frac{\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta\right)\left({a}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta+{c}^{\mathrm{2}} \right)}{\left({a}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \theta\right)\left({c}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \theta\right)} \\ $$$$=\left(\frac{{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{sin}\:^{\mathrm{2}} \theta\right)\left(\mathrm{sin}\:^{\mathrm{2}} \theta+\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$=\left(\mathrm{sin}\:^{\mathrm{4}} \theta+\mathrm{cos}\:^{\mathrm{4}} \theta+\mathrm{2sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:+\left(\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\mathrm{2}+\frac{{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} }\right)\mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{2}} \theta \\ $$$$=\mathrm{1}+\left(\frac{{c}}{{a}}−\frac{{a}}{{c}}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{2}} \theta\:\geqslant\:\mathrm{1}\: \\ $$$${Hence} \\ $$$$\:{AD}.{BC}\:\geqslant\:{AB}.{CD} \\ $$$$ \\ $$

Commented by Tinkutara last updated on 20/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by ajfour last updated on 19/Oct/17

((AD+BC)/(AB+CD)) =(((√(a^2 +c^2 tan^2 θ)) +(√(c^2 +a^2 tan^2 θ)))/((a+c)sec θ)) =(1/((a+c))) [(√(a^2 cos^2 θ+c^2 sin^2 θ)) + (√(c^2 cos^2 θ+a^2 sin^2 θ)) ] ......

$$\frac{{AD}+{BC}}{{AB}+{CD}}\:=\frac{\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta}\:+\sqrt{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta}}{\left({a}+{c}\right)\mathrm{sec}\:\theta} \\ $$$$=\frac{\mathrm{1}}{\left({a}+{c}\right)}\:\left[\sqrt{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{c}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\:+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{{c}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta+{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}\:\right] \\ $$$$...... \\ $$

Commented by mrW1 last updated on 19/Oct/17

Commented by mrW1 last updated on 19/Oct/17

AA′//CD//AB AA′′//CB DA′//AC//BA′′ DA′=AC=BA′′ AB+CD=AB+AA′=A′B=DA′′≤AD+AA′′=AD+BC

$$\mathrm{AA}'//\mathrm{CD}//\mathrm{AB} \\ $$$$\mathrm{AA}''//\mathrm{CB} \\ $$$$\mathrm{DA}'//\mathrm{AC}//\mathrm{BA}'' \\ $$$$\mathrm{DA}'=\mathrm{AC}=\mathrm{BA}'' \\ $$$$\mathrm{AB}+\mathrm{CD}=\mathrm{AB}+\mathrm{AA}'=\mathrm{A}'\mathrm{B}=\mathrm{DA}''\leqslant\mathrm{AD}+\mathrm{AA}''=\mathrm{AD}+\mathrm{BC} \\ $$

Commented by Tinkutara last updated on 20/Oct/17

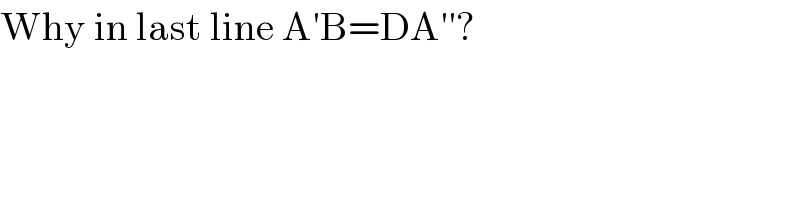
Why in last line A′B=DA′′?

$$\mathrm{Why}\:\mathrm{in}\:\mathrm{last}\:\mathrm{line}\:\mathrm{A}'\mathrm{B}=\mathrm{DA}''? \\ $$

Commented by mrW1 last updated on 20/Oct/17

Since DA′//CA//BA′′ and AC⊥DB, ⇒ΔA′DB and ΔA′′BD are right angled. Since DA′=BA′′=CA and DB=BD, ⇒BA′=DA′′

$$\mathrm{Since}\:\mathrm{DA}'//\mathrm{CA}//\mathrm{BA}''\:\mathrm{and}\:\mathrm{AC}\bot\mathrm{DB}, \\ $$$$\Rightarrow\Delta\mathrm{A}'\mathrm{DB}\:\mathrm{and}\:\Delta\mathrm{A}''\mathrm{BD}\:\mathrm{are}\:\mathrm{right}\:\mathrm{angled}. \\ $$$$\mathrm{Since}\:\mathrm{DA}'=\mathrm{BA}''=\mathrm{CA}\:\mathrm{and}\:\mathrm{DB}=\mathrm{BD}, \\ $$$$\Rightarrow\mathrm{BA}'=\mathrm{DA}'' \\ $$

Commented by Tinkutara last updated on 20/Oct/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Commented by ajfour last updated on 20/Oct/17

wonderful sir, thoughtful constructions.

$${wonderful}\:{sir},\:{thoughtful} \\ $$$${constructions}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com