
Question Number 22618 by Tinkutara last updated on 21/Oct/17
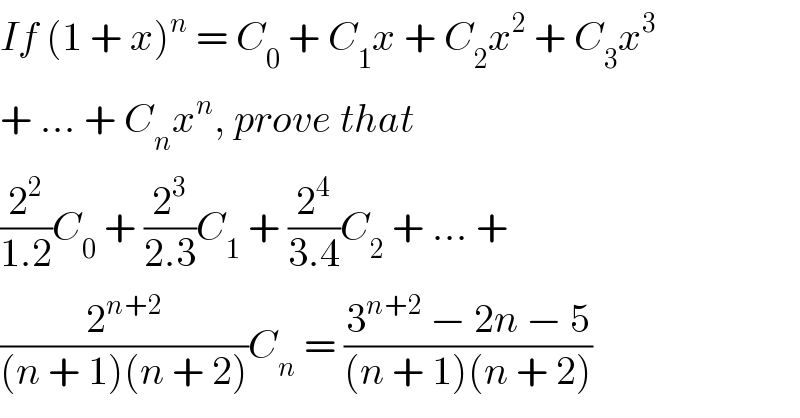
$${If}\:\left(\mathrm{1}\:+\:{x}\right)^{{n}} \:=\:{C}_{\mathrm{0}} \:+\:{C}_{\mathrm{1}} {x}\:+\:{C}_{\mathrm{2}} {x}^{\mathrm{2}} \:+\:{C}_{\mathrm{3}} {x}^{\mathrm{3}} \\ $$$$+\:...\:+\:{C}_{{n}} {x}^{{n}} ,\:{prove}\:{that} \\ $$$$\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1}.\mathrm{2}}{C}_{\mathrm{0}} \:+\:\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{2}.\mathrm{3}}{C}_{\mathrm{1}} \:+\:\frac{\mathrm{2}^{\mathrm{4}} }{\mathrm{3}.\mathrm{4}}{C}_{\mathrm{2}} \:+\:...\:+ \\ $$$$\frac{\mathrm{2}^{{n}+\mathrm{2}} }{\left({n}\:+\:\mathrm{1}\right)\left({n}\:+\:\mathrm{2}\right)}{C}_{{n}} \:=\:\frac{\mathrm{3}^{{n}+\mathrm{2}} \:−\:\mathrm{2}{n}\:−\:\mathrm{5}}{\left({n}\:+\:\mathrm{1}\right)\left({n}\:+\:\mathrm{2}\right)} \\ $$
Answered by ajfour last updated on 21/Oct/17
![∫_0 ^( x) (1+x)^n dx=((C_0 x)/1)+((C_1 x^2 )/2)+((C_2 x^3 )/3)+.. ⇒(((1+x)^(n+1) −1)/(n+1)) =((C_0 x)/1)+((C_1 x^2 )/2)+((C_3 x^3 )/3)+... ∫_0 ^( 2) (((1+x)^(n+1) −1)/(n+1))dx =((2^2 C_0 )/(1.2))+((2^3 C_1 )/(2.3))+.. =[(((1+x)^(n+2) −(n+2)x)/((n+1)(n+2)))]∣_0 ^2 =((3^(n+2) −2n−4−1)/((n+1)(n+2))) =((3^(n+2) −2n−5)/((n+1)(n+2))) .](Q22629.png)
$$\int_{\mathrm{0}} ^{\:\:{x}} \left(\mathrm{1}+{x}\right)^{{n}} {dx}=\frac{{C}_{\mathrm{0}} {x}}{\mathrm{1}}+\frac{{C}_{\mathrm{1}} {x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{C}_{\mathrm{2}} {x}^{\mathrm{3}} }{\mathrm{3}}+.. \\ $$$$\Rightarrow\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}\:=\frac{{C}_{\mathrm{0}} {x}}{\mathrm{1}}+\frac{{C}_{\mathrm{1}} {x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{C}_{\mathrm{3}} {x}^{\mathrm{3}} }{\mathrm{3}}+... \\ $$$$\int_{\mathrm{0}} ^{\:\:\mathrm{2}} \frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}{dx}\:=\frac{\mathrm{2}^{\mathrm{2}} {C}_{\mathrm{0}} }{\mathrm{1}.\mathrm{2}}+\frac{\mathrm{2}^{\mathrm{3}} {C}_{\mathrm{1}} }{\mathrm{2}.\mathrm{3}}+.. \\ $$$$=\left[\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{2}} −\left({n}+\mathrm{2}\right){x}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\right]\mid_{\mathrm{0}} ^{\mathrm{2}} \: \\ $$$$=\frac{\mathrm{3}^{{n}+\mathrm{2}} −\mathrm{2}{n}−\mathrm{4}−\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:\:=\frac{\mathrm{3}^{\boldsymbol{{n}}+\mathrm{2}} −\mathrm{2}\boldsymbol{{n}}−\mathrm{5}}{\left(\boldsymbol{{n}}+\mathrm{1}\right)\left(\boldsymbol{{n}}+\mathrm{2}\right)}\:. \\ $$
Commented by Tinkutara last updated on 21/Oct/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
