Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 22649 by ajfour last updated on 21/Oct/17

Commented by ajfour last updated on 21/Oct/17

solution to Q.22599

$${solution}\:{to}\:{Q}.\mathrm{22599} \\ $$

Answered by ajfour last updated on 21/Oct/17

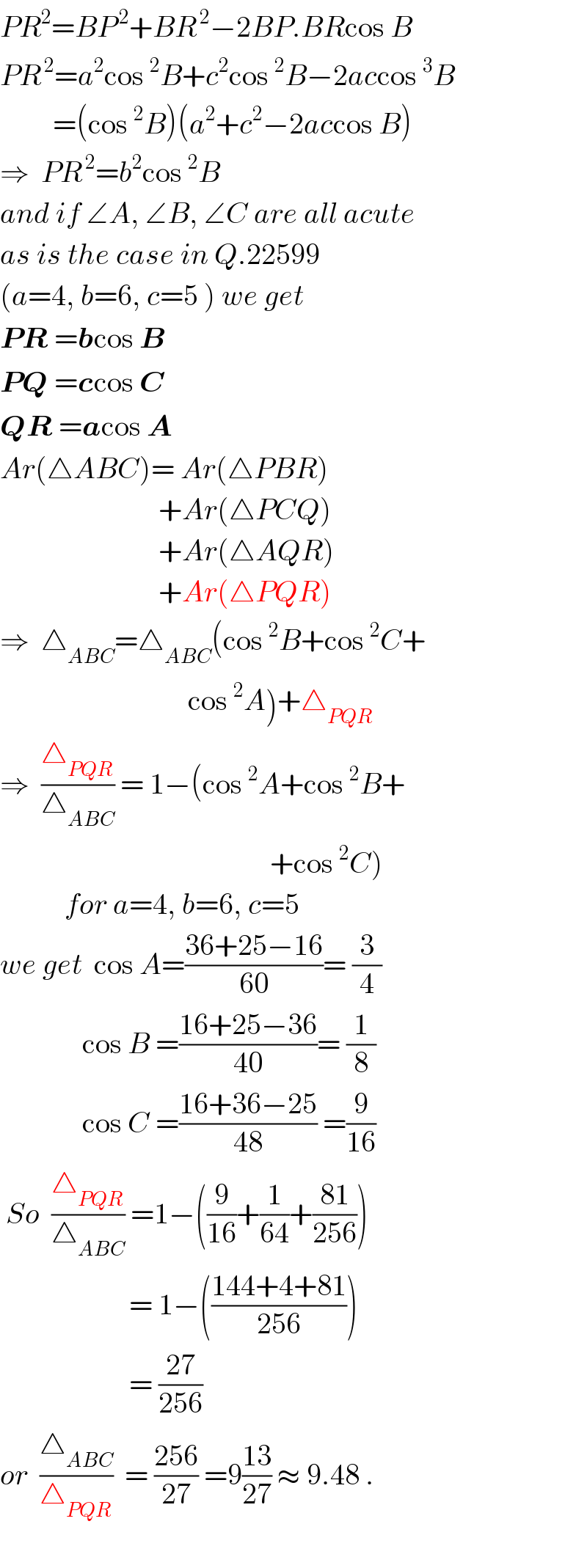
PR^2 =BP^( 2) +BR^( 2) −2BP.BRcos B PR^( 2) =a^2 cos^2 B+c^2 cos^2 B−2accos^3 B =(cos^2 B)(a^2 +c^2 −2accos B) ⇒ PR^( 2) =b^2 cos^2 B and if ∠A, ∠B, ∠C are all acute as is the case in Q.22599 (a=4, b=6, c=5 ) we get PR =bcos B PQ =ccos C QR =acos A Ar(△ABC)= Ar(△PBR) +Ar(△PCQ) +Ar(△AQR) +Ar(△PQR) ⇒ △_(ABC) =△_(ABC) (cos^2 B+cos^2 C+ cos^2 A)+△_(PQR) ⇒ (△_(PQR) /△_(ABC) ) = 1−(cos^2 A+cos^2 B+ +cos^2 C) for a=4, b=6, c=5 we get cos A=((36+25−16)/(60))= (3/4) cos B =((16+25−36)/(40))= (1/8) cos C =((16+36−25)/(48)) =(9/(16)) So (△_(PQR) /△_(ABC) ) =1−((9/(16))+(1/(64))+((81)/(256))) = 1−(((144+4+81)/(256))) = ((27)/(256)) or (△_(ABC) /△_(PQR) ) = ((256)/(27)) =9((13)/(27)) ≈ 9.48 .

$${PR}^{\mathrm{2}} ={BP}^{\:\mathrm{2}} +{BR}^{\:\mathrm{2}} −\mathrm{2}{BP}.{BR}\mathrm{cos}\:{B} \\ $$$${PR}^{\:\mathrm{2}} ={a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {B}+{c}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {B}−\mathrm{2}{ac}\mathrm{cos}\:^{\mathrm{3}} {B} \\ $$$$\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\:^{\mathrm{2}} {B}\right)\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}\mathrm{cos}\:{B}\right) \\ $$$$\Rightarrow\:\:{PR}^{\:\mathrm{2}} ={b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {B} \\ $$$${and}\:{if}\:\angle{A},\:\angle{B},\:\angle{C}\:{are}\:{all}\:{acute} \\ $$$${as}\:{is}\:{the}\:{case}\:{in}\:{Q}.\mathrm{22599} \\ $$$$\left({a}=\mathrm{4},\:{b}=\mathrm{6},\:{c}=\mathrm{5}\:\right)\:{we}\:{get} \\ $$$$\boldsymbol{{PR}}\:=\boldsymbol{{b}}\mathrm{cos}\:\boldsymbol{{B}} \\ $$$$\boldsymbol{{PQ}}\:=\boldsymbol{{c}}\mathrm{cos}\:\boldsymbol{{C}} \\ $$$$\boldsymbol{{QR}}\:=\boldsymbol{{a}}\mathrm{cos}\:\boldsymbol{{A}} \\ $$$${Ar}\left(\bigtriangleup{ABC}\right)=\:{Ar}\left(\bigtriangleup{PBR}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{Ar}\left(\bigtriangleup{PCQ}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{Ar}\left(\bigtriangleup{AQR}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{Ar}\left(\bigtriangleup{PQR}\right) \\ $$$$\Rightarrow\:\:\bigtriangleup_{{ABC}} =\bigtriangleup_{{ABC}} \left(\mathrm{cos}\:^{\mathrm{2}} {B}+\mathrm{cos}\:^{\mathrm{2}} {C}+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} {A}\right)+\bigtriangleup_{{PQR}} \\ $$$$\Rightarrow\:\:\frac{\bigtriangleup_{{PQR}} }{\bigtriangleup_{{ABC}} }\:=\:\mathrm{1}−\left(\mathrm{cos}\:^{\mathrm{2}} {A}+\mathrm{cos}\:^{\mathrm{2}} {B}+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{cos}\:^{\mathrm{2}} {C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{for}\:{a}=\mathrm{4},\:{b}=\mathrm{6},\:{c}=\mathrm{5} \\ $$$${we}\:{get}\:\:\mathrm{cos}\:{A}=\frac{\mathrm{36}+\mathrm{25}−\mathrm{16}}{\mathrm{60}}=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:{B}\:=\frac{\mathrm{16}+\mathrm{25}−\mathrm{36}}{\mathrm{40}}=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:{C}\:=\frac{\mathrm{16}+\mathrm{36}−\mathrm{25}}{\mathrm{48}}\:=\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\:{So}\:\:\frac{\bigtriangleup_{{PQR}} }{\bigtriangleup_{{ABC}} }\:=\mathrm{1}−\left(\frac{\mathrm{9}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{64}}+\frac{\mathrm{81}}{\mathrm{256}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\left(\frac{\mathrm{144}+\mathrm{4}+\mathrm{81}}{\mathrm{256}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{27}}{\mathrm{256}} \\ $$$${or}\:\:\frac{\bigtriangleup_{{ABC}} }{\bigtriangleup_{{PQR}} }\:\:=\:\frac{\mathrm{256}}{\mathrm{27}}\:=\mathrm{9}\frac{\mathrm{13}}{\mathrm{27}}\:\approx\:\mathrm{9}.\mathrm{48}\:. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 21/Oct/17

There is a very short method to prove that r=(R/2). We can find the angles of ΔPQR as: ∠P=π−2A ∠Q=π−2B ∠R=π−2C In original triangle let R_1 =(b/(2sin B)) Let R_2 be circumradius of pedal triangle. Then since we already found the sides, so R_2 =((PR)/(2sin Q))=((bcos B)/(2sin 2B))=(b/(4sin B))=(R_1 /2) Hence proved. I only forgot how to find the sides of pedal triangle. Then I recalled from here. Thanks very much ajfour Sir!

$${There}\:{is}\:{a}\:{very}\:{short}\:{method}\:{to} \\ $$$${prove}\:{that}\:{r}=\frac{{R}}{\mathrm{2}}. \\ $$$${We}\:{can}\:{find}\:{the}\:{angles}\:{of}\:\Delta{PQR}\:{as}: \\ $$$$\angle{P}=\pi−\mathrm{2}{A} \\ $$$$\angle{Q}=\pi−\mathrm{2}{B} \\ $$$$\angle{R}=\pi−\mathrm{2}{C} \\ $$$${In}\:{original}\:{triangle}\:{let}\:{R}_{\mathrm{1}} =\frac{{b}}{\mathrm{2sin}\:{B}} \\ $$$${Let}\:{R}_{\mathrm{2}} \:{be}\:{circumradius}\:{of}\:{pedal} \\ $$$${triangle}.\:{Then}\:{since}\:{we}\:{already} \\ $$$${found}\:{the}\:{sides},\:{so} \\ $$$${R}_{\mathrm{2}} =\frac{{PR}}{\mathrm{2sin}\:{Q}}=\frac{{b}\mathrm{cos}\:{B}}{\mathrm{2sin}\:\mathrm{2}{B}}=\frac{{b}}{\mathrm{4sin}\:{B}}=\frac{{R}_{\mathrm{1}} }{\mathrm{2}} \\ $$$${Hence}\:{proved}. \\ $$$${I}\:{only}\:{forgot}\:{how}\:{to}\:{find}\:{the}\:{sides}\:{of} \\ $$$${pedal}\:{triangle}.\:{Then}\:{I}\:{recalled}\:{from} \\ $$$${here}.\:{Thanks}\:{very}\:{much}\:{ajfour}\:{Sir}! \\ $$

Commented by ajfour last updated on 21/Oct/17

Very nice ; thanks .

$${Very}\:{nice}\:;\:{thanks}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com