
Question Number 229 by ssahoo last updated on 25/Jan/15
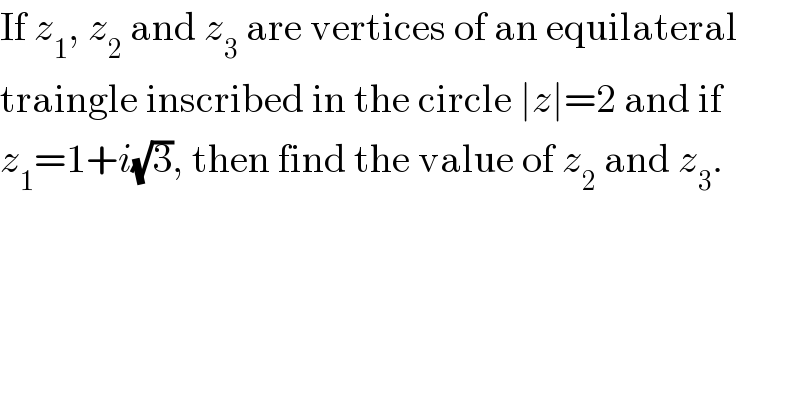
$$\mathrm{If}\:{z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} \:\mathrm{and}\:{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{an}\:\mathrm{equilateral} \\ $$$$\mathrm{traingle}\:\mathrm{inscribed}\:\mathrm{in}\:\mathrm{the}\:\mathrm{circle}\:\mid{z}\mid=\mathrm{2}\:\mathrm{and}\:\mathrm{if} \\ $$$${z}_{\mathrm{1}} =\mathrm{1}+{i}\sqrt{\mathrm{3}},\:\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{z}_{\mathrm{2}} \:\mathrm{and}\:{z}_{\mathrm{3}} . \\ $$
Answered by 123456 last updated on 16/Dec/14
![∣z_1 ∣=2 z_1 =(2/2)(1+i(√3)) =2((1/2)+i((√3)/2)) =2(cos (π/3)+isin (π/3)) =2e^((π/3)i) since z_1 ,z_2 ,z_3 are vertice of a equilatery triangle escribed into a circle at origin, then the other points are defased by ((2π)/3) then z_2 =z_1 e^(((2π)/3)i) =2e^((1+2)(π/3)i) =2e^(πi) =2(cos π+isin π) =−2 z_3 =z_2 e^(((2π)/3)i) =z_1 e^(−((2π)/3)i) =2e^(πi) e^(((2π)/3)i) =2e^((π/3)i) e^(−((2π)/3)i) =2e^((1+(2/3))πi) =2e^((1−2)(π/3)i) =2e^(((5π)/3)i) =2e^(−(π/3)i) =2(cos ((5π)/3)+isin ((5π)/3))=2(cos −(π/3)+isin −(π/3)) =2((1/2)−i((√3)/2))=2(cos (π/3)−isin (π/3)) =1−i(√3) so {z_1 ,z_2 ,z_3 }={1+i(√3),−2,1−i(√3)} solution of (a≠0) a[z−(1+i(√3))][z−(−2)][z−(1−i(√3))]=0 a[(z−1)−i(√3)][(z−1)+i(√3)](z+2)=0 a[(z−1)^2 +3](z+2)=0 a(z^2 −2z+1+3)(z+2)=0 a(z^2 −2z+4)(z+2)=0 a(z^3 −2z^2 +4z+2z^2 −4z+8)=0 a(z^3 +8)=0](Q232.png)
$$\mid{z}_{\mathrm{1}} \mid=\mathrm{2} \\ $$$${z}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{2}}\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right) \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{3}}+{i}\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}{e}^{\frac{\pi}{\mathrm{3}}{i}} \\ $$$$\mathrm{since}\:{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} ,{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{vertice}\:\mathrm{of}\:\mathrm{a}\:\mathrm{equilatery}\:\mathrm{triangle}\:\mathrm{escribed}\:\mathrm{into}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{at}\:\mathrm{origin},\:\mathrm{then}\:\mathrm{the}\:\mathrm{other}\:\mathrm{points}\:\mathrm{are}\:\mathrm{defased}\:\mathrm{by}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{then} \\ $$$${z}_{\mathrm{2}} ={z}_{\mathrm{1}} {e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} \\ $$$$=\mathrm{2}{e}^{\left(\mathrm{1}+\mathrm{2}\right)\frac{\pi}{\mathrm{3}}{i}} \\ $$$$=\mathrm{2}{e}^{\pi{i}} \\ $$$$=\mathrm{2}\left(\mathrm{cos}\:\pi+{i}\mathrm{sin}\:\pi\right) \\ $$$$=−\mathrm{2} \\ $$$${z}_{\mathrm{3}} ={z}_{\mathrm{2}} {e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} ={z}_{\mathrm{1}} {e}^{−\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} \\ $$$$=\mathrm{2}{e}^{\pi{i}} {e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} =\mathrm{2}{e}^{\frac{\pi}{\mathrm{3}}{i}} {e}^{−\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} \\ $$$$=\mathrm{2}{e}^{\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)\pi{i}} =\mathrm{2}{e}^{\left(\mathrm{1}−\mathrm{2}\right)\frac{\pi}{\mathrm{3}}{i}} \\ $$$$=\mathrm{2}{e}^{\frac{\mathrm{5}\pi}{\mathrm{3}}{i}} =\mathrm{2}{e}^{−\frac{\pi}{\mathrm{3}}{i}} \\ $$$$=\mathrm{2}\left(\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{3}}+{i}\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{3}}\right)=\mathrm{2}\left(\mathrm{cos}\:−\frac{\pi}{\mathrm{3}}+{i}\mathrm{sin}\:−\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=\mathrm{2}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{3}}−{i}\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{1}−{i}\sqrt{\mathrm{3}} \\ $$$$\mathrm{so} \\ $$$$\left\{{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} ,{z}_{\mathrm{3}} \right\}=\left\{\mathrm{1}+{i}\sqrt{\mathrm{3}},−\mathrm{2},\mathrm{1}−{i}\sqrt{\mathrm{3}}\right\} \\ $$$$\mathrm{solution}\:\mathrm{of}\:\left({a}\neq\mathrm{0}\right) \\ $$$${a}\left[{z}−\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)\right]\left[{z}−\left(−\mathrm{2}\right)\right]\left[{z}−\left(\mathrm{1}−{i}\sqrt{\mathrm{3}}\right)\right]=\mathrm{0} \\ $$$${a}\left[\left({z}−\mathrm{1}\right)−{i}\sqrt{\mathrm{3}}\right]\left[\left({z}−\mathrm{1}\right)+{i}\sqrt{\mathrm{3}}\right]\left({z}+\mathrm{2}\right)=\mathrm{0} \\ $$$${a}\left[\left({z}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\right]\left({z}+\mathrm{2}\right)=\mathrm{0} \\ $$$${a}\left({z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{1}+\mathrm{3}\right)\left({z}+\mathrm{2}\right)=\mathrm{0} \\ $$$${a}\left({z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{4}\right)\left({z}+\mathrm{2}\right)=\mathrm{0} \\ $$$${a}\left({z}^{\mathrm{3}} −\mathrm{2}{z}^{\mathrm{2}} +\mathrm{4}{z}+\mathrm{2}{z}^{\mathrm{2}} −\mathrm{4}{z}+\mathrm{8}\right)=\mathrm{0} \\ $$$${a}\left({z}^{\mathrm{3}} +\mathrm{8}\right)=\mathrm{0} \\ $$
