Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 23036 by ajfour last updated on 25/Oct/17

Commented by mrW1 last updated on 25/Oct/17

(([PQRSTU])/([ABCDEF]))=(1/7)

$$\frac{\left[\boldsymbol{{PQRSTU}}\right]}{\left[\boldsymbol{{ABCDEF}}\right]}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$

Commented by ajfour last updated on 25/Oct/17

The blue line segment from A starts at A and ends in midpoint of OE, blue line segment from B ends in midpoint of OF,.. and so on. Find ratio area of regular hexagon PQRSTU so formed, to the area of given regular hexagon ABCDEF of side a.

$${The}\:{blue}\:{line}\:{segment}\:{from}\:{A} \\ $$$${starts}\:{at}\:{A}\:{and}\:{ends}\:{in}\:{midpoint} \\ $$$${of}\:{OE},\:{blue}\:{line}\:{segment}\:{from}\:{B} \\ $$$${ends}\:{in}\:{midpoint}\:{of}\:{OF},..\:{and} \\ $$$${so}\:{on}.\:{Find}\:{ratio}\:\boldsymbol{{area}}\:\boldsymbol{{of}}\:{regular} \\ $$$${hexagon}\:\boldsymbol{{PQRSTU}}\:{so}\:{formed}, \\ $$$${to}\:{the}\:\boldsymbol{{area}}\:\boldsymbol{{of}}\:{given}\:{regular} \\ $$$${hexagon}\:\boldsymbol{{ABCDEF}}\:{of}\:{side}\:\boldsymbol{{a}}. \\ $$

Commented by ajfour last updated on 25/Oct/17

Pleaze explain Sir. I created this question myself, haven′t even attempted, nice answer sir. It will take a long method if i solve with vectord or coordinate geometry. Kindly explain your way sir.

$${Pleaze}\:{explain}\:{Sir}. \\ $$$${I}\:{created}\:{this}\:{question}\:{myself}, \\ $$$${haven}'{t}\:{even}\:{attempted},\:{nice} \\ $$$${answer}\:{sir}.\:{It}\:{will}\:{take}\:{a}\:{long} \\ $$$${method}\:{if}\:{i}\:{solve}\:{with}\:{vectord} \\ $$$${or}\:{coordinate}\:{geometry}. \\ $$$${Kindly}\:{explain}\:{your}\:{way}\:{sir}. \\ $$

Commented by mrW1 last updated on 25/Oct/17

Commented by mrW1 last updated on 25/Oct/17

let a=1 to make the writing easier. OE=OD=...=a=1 OL=ON=...=(a/2)=(1/2) EN^2 =1^2 +((1/2))^2 −2×1×(1/2)×cos 120°=1+(1/4)+(1/2)=(7/4) ⇒EN=((√7)/2) OK is the angle bisector of ∠EON, ⇒((EK)/(KN))=((OE)/(ON))=2 ⇒EK=(2/3)×EN=(2/3)×((√7)/2)=((√7)/3) ⇒KN=(1/3)×EN=(1/3)×((√7)/2)=((√7)/6) { EK^2 =OE^2 +OK^2 −2×OE×OK×cos 60° (7/9)=1+OK^2 −2×1×OK×(1/2) OK^2 −OK+(2/9)=0 ⇒OK=(1/2)(1±(√(1−(8/9))))=(1/2)(1±(1/3))=((3±1)/6)= { ((1/3)),((2/3)) :} only (1/3) is suitable for us. ⇒OK=(1/3) } (one can also directly use formula for angle bisector to get OK instead of {...}) KD=OD−OK=1−(1/3)=(2/3) ΔDKR∼ΔEKO ((KR)/(KD))=((OK)/(EK)) ⇒KR=(1/3)×(3/(√7))×(2/3)=((2(√7))/(21)) ((RD)/(KD))=((OK)/(EO)) ⇒RD=((1×3)/(√7))×(2/3)=((2(√7))/7) RM=DM−RD=EK−RD=((√7)/3)−((2(√7))/7)=((√7)/(21)) SR=SK+KR=RM+KR=((√7)/(21))+((2(√7))/(21))=((√7)/7) =side length of the small hexagon (A_(small) /A_(big) )=(((side length small)/(side length big)))^2 =(((((√7)/7)a)/a))^2 =(1/7)

$$\mathrm{let}\:\mathrm{a}=\mathrm{1}\:\mathrm{to}\:\mathrm{make}\:\mathrm{the}\:\mathrm{writing}\:\mathrm{easier}. \\ $$$$ \\ $$$$\mathrm{OE}=\mathrm{OD}=...=\mathrm{a}=\mathrm{1} \\ $$$$\mathrm{OL}=\mathrm{ON}=...=\frac{\mathrm{a}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{EN}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{cos}\:\mathrm{120}°=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{EN}=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{OK}\:\mathrm{is}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{bisector}\:\mathrm{of}\:\angle\mathrm{EON}, \\ $$$$\Rightarrow\frac{\mathrm{EK}}{\mathrm{KN}}=\frac{\mathrm{OE}}{\mathrm{ON}}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{EK}=\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{EN}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{KN}=\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{EN}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{6}} \\ $$$$\left\{\right. \\ $$$$\mathrm{EK}^{\mathrm{2}} =\mathrm{OE}^{\mathrm{2}} +\mathrm{OK}^{\mathrm{2}} −\mathrm{2}×\mathrm{OE}×\mathrm{OK}×\mathrm{cos}\:\mathrm{60}° \\ $$$$\frac{\mathrm{7}}{\mathrm{9}}=\mathrm{1}+\mathrm{OK}^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\mathrm{OK}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{OK}^{\mathrm{2}} −\mathrm{OK}+\frac{\mathrm{2}}{\mathrm{9}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{OK}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\pm\sqrt{\mathrm{1}−\frac{\mathrm{8}}{\mathrm{9}}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\pm\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{3}\pm\mathrm{1}}{\mathrm{6}}=\begin{cases}{\frac{\mathrm{1}}{\mathrm{3}}}\\{\frac{\mathrm{2}}{\mathrm{3}}}\end{cases} \\ $$$$\mathrm{only}\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{is}\:\mathrm{suitable}\:\mathrm{for}\:\mathrm{us}. \\ $$$$\Rightarrow\mathrm{OK}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left.\right\} \\ $$$$\left(\mathrm{one}\:\mathrm{can}\:\mathrm{also}\:\mathrm{directly}\:\mathrm{use}\:\mathrm{formula}\:\mathrm{for}\right. \\ $$$$\left.\mathrm{angle}\:\mathrm{bisector}\:\mathrm{to}\:\mathrm{get}\:\mathrm{OK}\:\mathrm{instead}\:\mathrm{of}\:\left\{...\right\}\right) \\ $$$$\mathrm{KD}=\mathrm{OD}−\mathrm{OK}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$\Delta\mathrm{DKR}\sim\Delta\mathrm{EKO} \\ $$$$\frac{\mathrm{KR}}{\mathrm{KD}}=\frac{\mathrm{OK}}{\mathrm{EK}} \\ $$$$\Rightarrow\mathrm{KR}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}}{\sqrt{\mathrm{7}}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{21}} \\ $$$$\frac{\mathrm{RD}}{\mathrm{KD}}=\frac{\mathrm{OK}}{\mathrm{EO}} \\ $$$$\Rightarrow\mathrm{RD}=\frac{\mathrm{1}×\mathrm{3}}{\sqrt{\mathrm{7}}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{7}} \\ $$$$\mathrm{RM}=\mathrm{DM}−\mathrm{RD}=\mathrm{EK}−\mathrm{RD}=\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}−\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{7}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{21}} \\ $$$$ \\ $$$$\mathrm{SR}=\mathrm{SK}+\mathrm{KR}=\mathrm{RM}+\mathrm{KR}=\frac{\sqrt{\mathrm{7}}}{\mathrm{21}}+\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{21}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{7}} \\ $$$$=\mathrm{side}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{small}\:\mathrm{hexagon} \\ $$$$ \\ $$$$\frac{\mathrm{A}_{\mathrm{small}} }{\mathrm{A}_{\mathrm{big}} }=\left(\frac{\mathrm{side}\:\mathrm{length}\:\mathrm{small}}{\mathrm{side}\:\mathrm{length}\:\mathrm{big}}\right)^{\mathrm{2}} =\left(\frac{\frac{\sqrt{\mathrm{7}}}{\mathrm{7}}\mathrm{a}}{\mathrm{a}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{7}} \\ $$

Commented by ajfour last updated on 25/Oct/17

thank you sir, but i shall also attempt now. Vector way.. perhaps!

$${thank}\:{you}\:{sir},\:{but}\:{i}\:{shall}\:{also} \\ $$$${attempt}\:{now}.\:{Vector}\:{way}.. \\ $$$${perhaps}! \\ $$

Commented by mrW1 last updated on 25/Oct/17

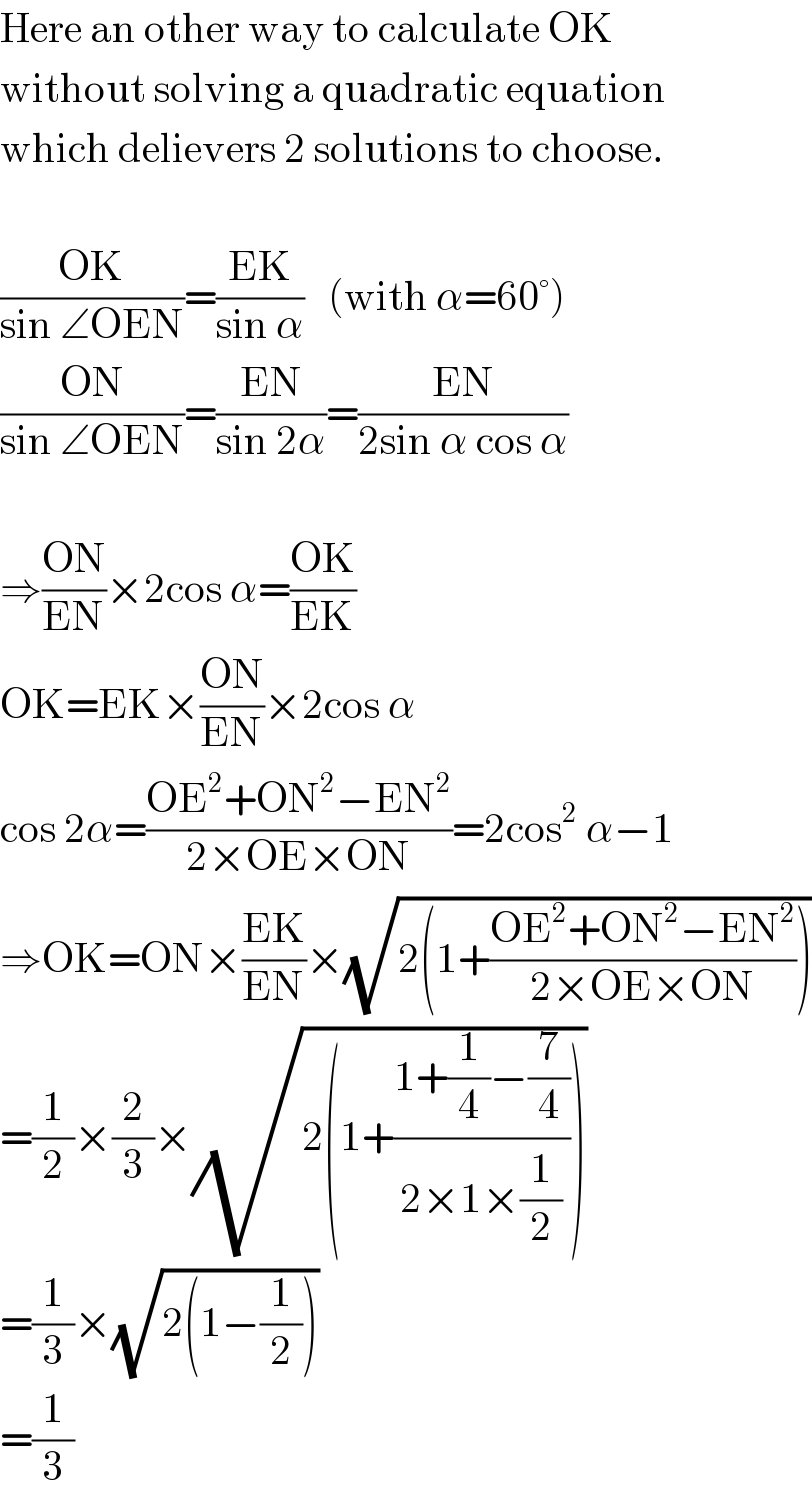
Here an other way to calculate OK without solving a quadratic equation which delievers 2 solutions to choose. ((OK)/(sin ∠OEN))=((EK)/(sin α)) (with α=60°) ((ON)/(sin ∠OEN))=((EN)/(sin 2α))=((EN)/(2sin α cos α)) ⇒((ON)/(EN))×2cos α=((OK)/(EK)) OK=EK×((ON)/(EN))×2cos α cos 2α=((OE^2 +ON^2 −EN^2 )/(2×OE×ON))=2cos^2 α−1 ⇒OK=ON×((EK)/(EN))×(√(2(1+((OE^2 +ON^2 −EN^2 )/(2×OE×ON))))) =(1/2)×(2/3)×(√(2(1+((1+(1/4)−(7/4))/(2×1×(1/2)))))) =(1/3)×(√(2(1−(1/2)))) =(1/3)

$$\mathrm{Here}\:\mathrm{an}\:\mathrm{other}\:\mathrm{way}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{OK} \\ $$$$\mathrm{without}\:\mathrm{solving}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{equation} \\ $$$$\mathrm{which}\:\mathrm{delievers}\:\mathrm{2}\:\mathrm{solutions}\:\mathrm{to}\:\mathrm{choose}. \\ $$$$ \\ $$$$\frac{\mathrm{OK}}{\mathrm{sin}\:\angle\mathrm{OEN}}=\frac{\mathrm{EK}}{\mathrm{sin}\:\alpha}\:\:\:\left(\mathrm{with}\:\alpha=\mathrm{60}°\right) \\ $$$$\frac{\mathrm{ON}}{\mathrm{sin}\:\angle\mathrm{OEN}}=\frac{\mathrm{EN}}{\mathrm{sin}\:\mathrm{2}\alpha}=\frac{\mathrm{EN}}{\mathrm{2sin}\:\alpha\:\mathrm{cos}\:\alpha} \\ $$$$ \\ $$$$\Rightarrow\frac{\mathrm{ON}}{\mathrm{EN}}×\mathrm{2cos}\:\alpha=\frac{\mathrm{OK}}{\mathrm{EK}} \\ $$$$\mathrm{OK}=\mathrm{EK}×\frac{\mathrm{ON}}{\mathrm{EN}}×\mathrm{2cos}\:\alpha \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\frac{\mathrm{OE}^{\mathrm{2}} +\mathrm{ON}^{\mathrm{2}} −\mathrm{EN}^{\mathrm{2}} }{\mathrm{2}×\mathrm{OE}×\mathrm{ON}}=\mathrm{2cos}^{\mathrm{2}} \:\alpha−\mathrm{1} \\ $$$$\Rightarrow\mathrm{OK}=\mathrm{ON}×\frac{\mathrm{EK}}{\mathrm{EN}}×\sqrt{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{OE}^{\mathrm{2}} +\mathrm{ON}^{\mathrm{2}} −\mathrm{EN}^{\mathrm{2}} }{\mathrm{2}×\mathrm{OE}×\mathrm{ON}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}×\sqrt{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{7}}{\mathrm{4}}}{\mathrm{2}×\mathrm{1}×\frac{\mathrm{1}}{\mathrm{2}}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\sqrt{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by ajfour last updated on 25/Oct/17

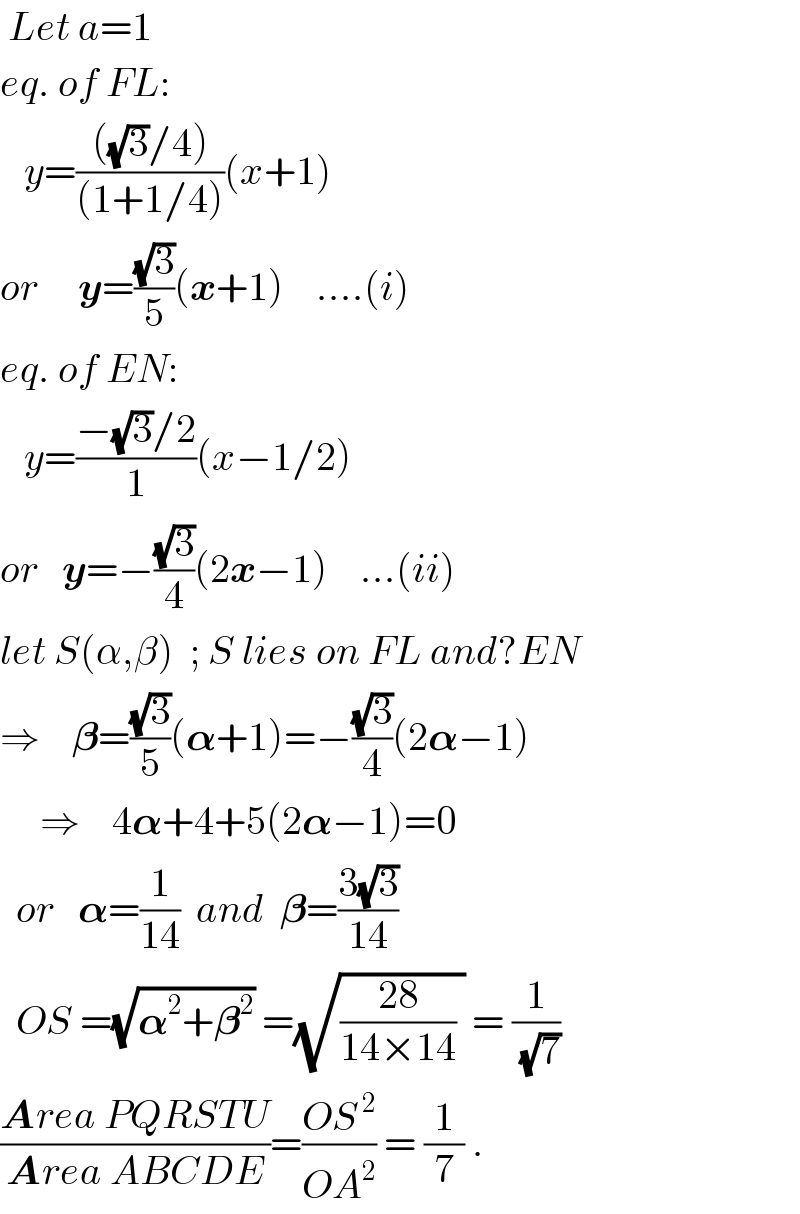
Let a=1 eq. of FL: y=((((√3)/4))/((1+1/4)))(x+1) or y=((√3)/5)(x+1) ....(i) eq. of EN: y=((−(√3)/2)/1)(x−1/2) or y=−((√3)/4)(2x−1) ...(ii) let S(α,β) ; S lies on FL and?EN ⇒ 𝛃=((√3)/5)(𝛂+1)=−((√3)/4)(2𝛂−1) ⇒ 4𝛂+4+5(2𝛂−1)=0 or 𝛂=(1/(14)) and 𝛃=((3(√3))/(14)) OS =(√(𝛂^2 +𝛃^2 )) =(√(((28)/(14×14)) )) = (1/(√7)) ((Area PQRSTU)/(Area ABCDE))=((OS^( 2) )/(OA^2 )) = (1/7) .

$$\:{Let}\:{a}=\mathrm{1} \\ $$$${eq}.\:{of}\:{FL}: \\ $$$$\:\:\:{y}=\frac{\left(\sqrt{\mathrm{3}}/\mathrm{4}\right)}{\left(\mathrm{1}+\mathrm{1}/\mathrm{4}\right)}\left({x}+\mathrm{1}\right) \\ $$$${or}\:\:\:\:\:\boldsymbol{{y}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{5}}\left(\boldsymbol{{x}}+\mathrm{1}\right)\:\:\:\:....\left({i}\right) \\ $$$${eq}.\:{of}\:{EN}: \\ $$$$\:\:\:{y}=\frac{−\sqrt{\mathrm{3}}/\mathrm{2}}{\mathrm{1}}\left({x}−\mathrm{1}/\mathrm{2}\right) \\ $$$${or}\:\:\:\boldsymbol{{y}}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{2}\boldsymbol{{x}}−\mathrm{1}\right)\:\:\:\:...\left({ii}\right) \\ $$$${let}\:{S}\left(\alpha,\beta\right)\:\:;\:{S}\:{lies}\:{on}\:{FL}\:{and}?{EN} \\ $$$$\Rightarrow\:\:\:\:\boldsymbol{\beta}=\frac{\sqrt{\mathrm{3}}}{\mathrm{5}}\left(\boldsymbol{\alpha}+\mathrm{1}\right)=−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{2}\boldsymbol{\alpha}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\Rightarrow\:\:\:\:\mathrm{4}\boldsymbol{\alpha}+\mathrm{4}+\mathrm{5}\left(\mathrm{2}\boldsymbol{\alpha}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:{or}\:\:\:\boldsymbol{\alpha}=\frac{\mathrm{1}}{\mathrm{14}}\:\:{and}\:\:\boldsymbol{\beta}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{14}} \\ $$$$\:\:{OS}\:=\sqrt{\boldsymbol{\alpha}^{\mathrm{2}} +\boldsymbol{\beta}^{\mathrm{2}} }\:=\sqrt{\frac{\mathrm{28}}{\mathrm{14}×\mathrm{14}}\:}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{7}}} \\ $$$$\frac{\boldsymbol{{A}}{rea}\:{PQRSTU}}{\boldsymbol{{A}}{rea}\:{ABCDE}}=\frac{{OS}^{\:\mathrm{2}} }{{OA}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{7}}\:. \\ $$

Commented by mrW1 last updated on 25/Oct/17

very nice way!

$$\mathrm{very}\:\mathrm{nice}\:\mathrm{way}! \\ $$

Commented by math solver last updated on 25/Oct/17

sir , in eq. of FL , while writing slope i didn′t get the numerator?? i think numerator should be tan30×(5/4)=5/4 ×(√( 3))

$${sir}\:,\:{in}\:{eq}.\:{of}\:{FL}\:,\:{while}\:{writing}\:{slope} \\ $$$${i}\:{didn}'{t}\:{get}\:{the}\:{numerator}?? \\ $$$${i}\:{think}\:{numerator}\:{should}\:{be}\: \\ $$$${tan}\mathrm{30}×\frac{\mathrm{5}}{\mathrm{4}}=\mathrm{5}/\mathrm{4}\:×\sqrt{\:\mathrm{3}} \\ $$

Commented by ajfour last updated on 25/Oct/17

yes.

$${yes}. \\ $$

Commented by ajfour last updated on 25/Oct/17

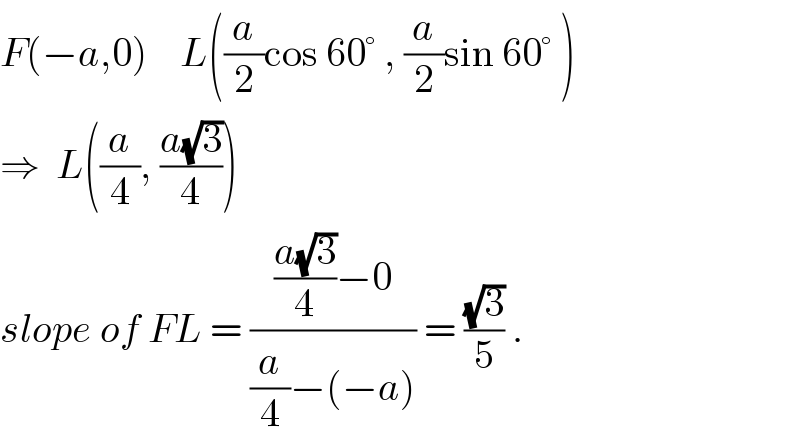
F(−a,0) L((a/2)cos 60° , (a/2)sin 60° ) ⇒ L((a/4), ((a(√3))/4)) slope of FL = ((((a(√3))/4)−0)/((a/4)−(−a))) = ((√3)/5) .

$${F}\left(−{a},\mathrm{0}\right)\:\:\:\:{L}\left(\frac{{a}}{\mathrm{2}}\mathrm{cos}\:\mathrm{60}°\:,\:\frac{{a}}{\mathrm{2}}\mathrm{sin}\:\mathrm{60}°\:\right) \\ $$$$\Rightarrow\:\:{L}\left(\frac{{a}}{\mathrm{4}},\:\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$${slope}\:{of}\:{FL}\:=\:\frac{\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{4}}−\mathrm{0}}{\frac{{a}}{\mathrm{4}}−\left(−{a}\right)}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{5}}\:. \\ $$

Commented by math solver last updated on 25/Oct/17

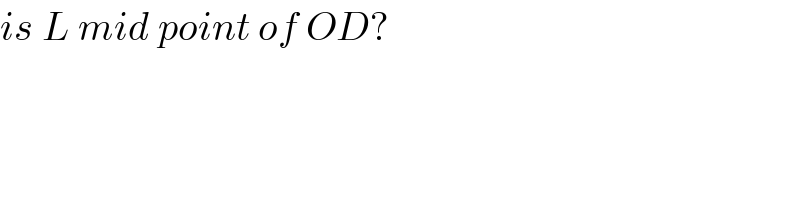
is L mid point of OD?

$${is}\:{L}\:{mid}\:{point}\:{of}\:{OD}? \\ $$

Commented by math solver last updated on 25/Oct/17

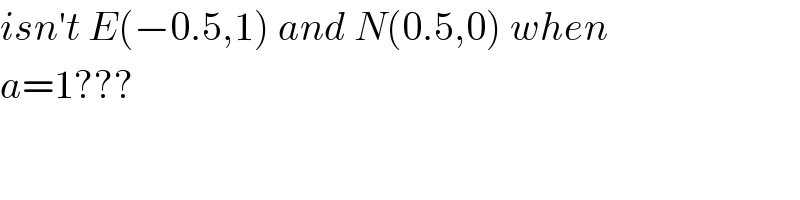
isn′t E(−0.5,1) and N(0.5,0) when a=1???

$${isn}'{t}\:{E}\left(−\mathrm{0}.\mathrm{5},\mathrm{1}\right)\:{and}\:{N}\left(\mathrm{0}.\mathrm{5},\mathrm{0}\right)\:{when}\: \\ $$$${a}=\mathrm{1}??? \\ $$

Commented by ajfour last updated on 26/Oct/17

E(−0.5, ((√3)/2))

$${E}\left(−\mathrm{0}.\mathrm{5},\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\: \\ $$

Commented by math solver last updated on 26/Oct/17

ok , i got it now . thanks!

$$\mathrm{ok}\:,\:\mathrm{i}\:\mathrm{got}\:\mathrm{it}\:\mathrm{now}\:. \\ $$$$\mathrm{thanks}! \\ $$

Answered by Tinkutara last updated on 26/Oct/17

Commented by Tinkutara last updated on 26/Oct/17

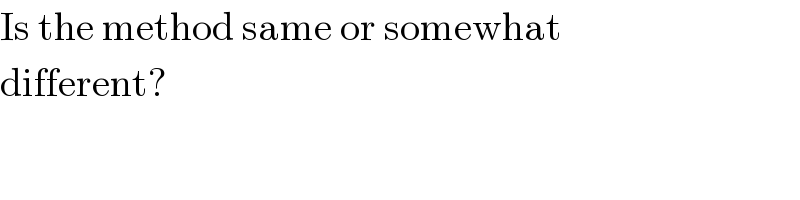
Is the method same or somewhat different?

$$\mathrm{Is}\:\mathrm{the}\:\mathrm{method}\:\mathrm{same}\:\mathrm{or}\:\mathrm{somewhat} \\ $$$$\mathrm{different}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com