Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2326 by Filup last updated on 16/Nov/15

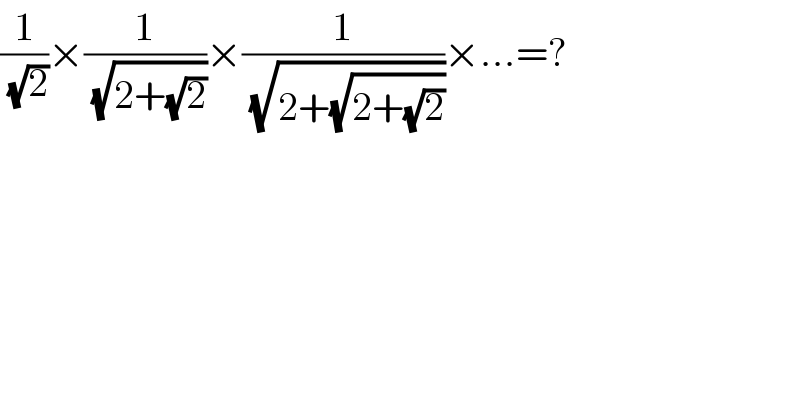
(1/(√2))×(1/(√(2+(√2))))×(1/(√(2+(√(2+(√2))))))×...=?

$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}×...=? \\ $$

Commented by Rasheed Soomro last updated on 16/Nov/15

Nice Approach!

$$\mathcal{N}{ice}\:\mathcal{A}{pproach}! \\ $$

Commented by Yozzi last updated on 16/Nov/15

a_1 =(1/(√2)),a_2 =(1/(√(2+a_1 ^(−1) )))=(1/(√(2+(√2)))) a_3 =(1/(√(2+a_2 ^(−1) )))=(1/(√(2+(√(2+(√2)))))) ∴ Recurrence relation for terms in product, n≥1, a_(n+1) =(1/(√(2+(1/a_n ))))=(√(a_n /(2a_n +1))),a_1 =(1/(√2)) a_(n+1) ^2 =(a_n /(2a_n +1))⇒2a_n a_(n+1) ^2 +a_(n+1) ^2 =a_n If convergence is assumed,l=a_n =a_(n+1) 2l^3 +l^2 −l=0 l(2l^2 +l−1)=0 ⇒l=0 ∨ 2l^2 +l−1=0 ⇒l=((−1±(√(1^2 −4×2×(−1))))/4)=((−1±3)/4) l=0.5 ∨ l=−1 ∨ l=0. Since a_n >0 ∀n≥1,⇒l=0.5 Then, the product summarised as Π_(i=1) ^∞ a_i →0 since the terms in the product approximate to 0.5<1 for a very large number of terms⇒(0.5)^∞ =0. This result is based on the assumption that a limit exists for {a_n }.

$${a}_{\mathrm{1}} =\frac{\mathrm{1}}{\sqrt{\mathrm{2}}},{a}_{\mathrm{2}} =\frac{\mathrm{1}}{\sqrt{\mathrm{2}+{a}_{\mathrm{1}} ^{−\mathrm{1}} }}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{1}}{\sqrt{\mathrm{2}+{a}_{\mathrm{2}} ^{−\mathrm{1}} }}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}} \\ $$$$\therefore\:{Recurrence}\:{relation}\:{for}\:{terms}\: \\ $$$${in}\:{product},\:{n}\geqslant\mathrm{1}, \\ $$$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\frac{\mathrm{1}}{{a}_{{n}} }}}=\sqrt{\frac{{a}_{{n}} }{\mathrm{2}{a}_{{n}} +\mathrm{1}}},{a}_{\mathrm{1}} =\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$${a}_{{n}+\mathrm{1}} ^{\mathrm{2}} =\frac{{a}_{{n}} }{\mathrm{2}{a}_{{n}} +\mathrm{1}}\Rightarrow\mathrm{2}{a}_{{n}} {a}_{{n}+\mathrm{1}} ^{\mathrm{2}} +{a}_{{n}+\mathrm{1}} ^{\mathrm{2}} ={a}_{{n}} \\ $$$${If}\:{convergence}\:{is}\:{assumed},{l}={a}_{{n}} ={a}_{{n}+\mathrm{1}} \\ $$$$\mathrm{2}{l}^{\mathrm{3}} +{l}^{\mathrm{2}} −{l}=\mathrm{0} \\ $$$${l}\left(\mathrm{2}{l}^{\mathrm{2}} +{l}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{l}=\mathrm{0}\:\vee\:\mathrm{2}{l}^{\mathrm{2}} +{l}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{l}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}^{\mathrm{2}} −\mathrm{4}×\mathrm{2}×\left(−\mathrm{1}\right)}}{\mathrm{4}}=\frac{−\mathrm{1}\pm\mathrm{3}}{\mathrm{4}} \\ $$$${l}=\mathrm{0}.\mathrm{5}\:\vee\:{l}=−\mathrm{1}\:\vee\:{l}=\mathrm{0}. \\ $$$${Since}\:{a}_{{n}} >\mathrm{0}\:\forall{n}\geqslant\mathrm{1},\Rightarrow{l}=\mathrm{0}.\mathrm{5} \\ $$$${Then},\:{the}\:{product}\:{summarised}\:{as} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\prod}}{a}_{{i}} \rightarrow\mathrm{0}\:{since}\:{the}\:{terms}\:{in}\:{the}\: \\ $$$${product}\:{approximate}\:{to}\:\mathrm{0}.\mathrm{5}<\mathrm{1}\:{for}\:{a}\:{very}\:{large}\: \\ $$$${number}\:{of}\:{terms}\Rightarrow\left(\mathrm{0}.\mathrm{5}\right)^{\infty} =\mathrm{0}.\:{This}\:{result}\:{is}\:{based} \\ $$$${on}\:{the}\:{assumption}\:{that}\:{a}\:{limit}\:{exists} \\ $$$${for}\:\left\{{a}_{{n}} \right\}. \\ $$

Answered by prakash jain last updated on 16/Nov/15

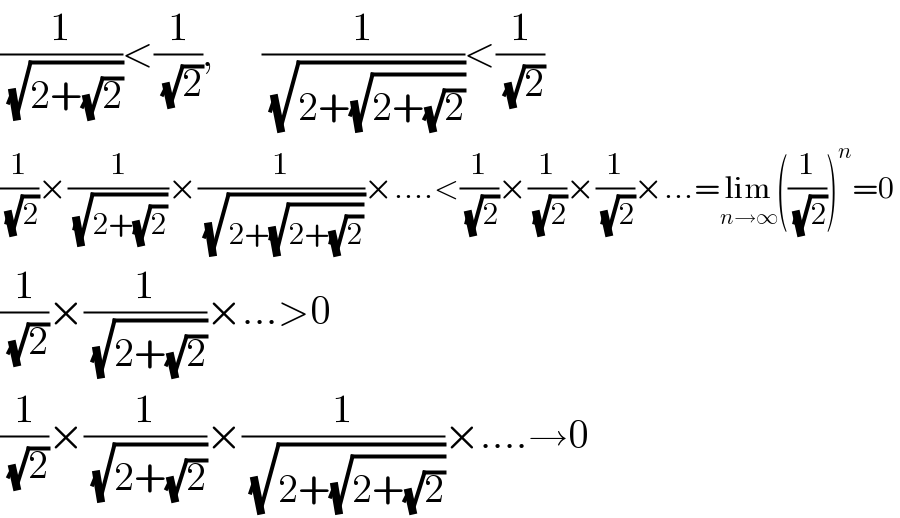
(1/(√(2+(√2))))<(1/(√2)), (1/(√(2+(√(2+(√2))))))<(1/(√2)) (1/(√2))×(1/(√(2+(√2))))×(1/(√(2+(√(2+(√2))))))×....<(1/(√2))×(1/(√2))×(1/(√2))×...=lim_(n→∞) ((1/(√2)))^n =0 (1/(√2))×(1/(√(2+(√2))))×...>0 (1/(√2))×(1/(√(2+(√2))))×(1/(√(2+(√(2+(√2))))))×....→0

$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}<\frac{\mathrm{1}}{\sqrt{\mathrm{2}}},\:\:\:\:\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}<\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}×....<\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×...=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{{n}} =\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}×...>\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}×....\rightarrow\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com