Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2334 by Syaka last updated on 16/Nov/15

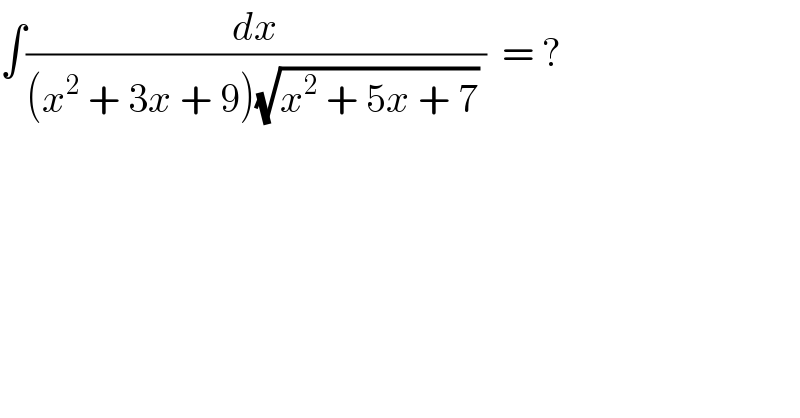
∫(dx/((x^2 + 3x + 9)(√(x^2 + 5x + 7)) )) = ?

$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\:+\:\mathrm{9}\right)\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{5}{x}\:+\:\mathrm{7}}\:}\:\:=\:? \\ $$

Commented by prakash jain last updated on 16/Nov/15

x^2 +5x+7=(x+(5/2))^2 +(3/4) x+(5/2)=((√3)/2)isin u dx=((√3)/2)icos u du (√((x+(5/2))^2 +(3/4) ))=(√(−(3/4)sin^2 u+(3/4))) =((√3)/2)cos u x^2 +3x+9=(x+(5/2))^2 −2x+((11)/4) =−(3/4)sin^2 u−2(((√3)/2)isin u−(5/2))+((11)/4) =−(1/4)(3sin^2 u+4i(√3)sin u−31) Integral to be computed −(i/4)∫ (du/((3sin^2 u+4(√3)isin u−31))) =((−i)/4)∫ (du/((3sin^2 u+4(√3)isin u+(2i)^2 )−27)) =((−i)/4)∫ (du/(((√3)sin u+2i)^2 −(3(√3))^2 )) =((−i)/4)∫(du/(((√3)sin u+2i−3(√3))((√3)sin u+2k+3(√3)))) =((−i)/(4∙6(√3)))[∫(du/(((√3)sin u+2i−3(√3))))−∫(du/((√3)sin u+2i+3(√3)))] =((−i)/(4∙6∙3))[∫(du/((sin u+((2/(√3))i−3)))−∫(du/(sin u+((2/(√3))i+3)))]

$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{7}=\left({x}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${x}+\frac{\mathrm{5}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\mathrm{sin}\:{u} \\ $$$${dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\mathrm{cos}\:{u}\:{du} \\ $$$$\sqrt{\left({x}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\:}=\sqrt{−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \:{u}+\frac{\mathrm{3}}{\mathrm{4}}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{u} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{9}=\left({x}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}{x}+\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} {u}−\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\mathrm{sin}\:{u}−\frac{\mathrm{5}}{\mathrm{2}}\right)+\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3sin}^{\mathrm{2}} {u}+\mathrm{4}{i}\sqrt{\mathrm{3}}\mathrm{sin}\:{u}−\mathrm{31}\right) \\ $$$$\mathrm{Integral}\:\mathrm{to}\:\mathrm{be}\:\mathrm{computed} \\ $$$$−\frac{{i}}{\mathrm{4}}\int\:\frac{{du}}{\left(\mathrm{3sin}^{\mathrm{2}} {u}+\mathrm{4}\sqrt{\mathrm{3}}{i}\mathrm{sin}\:{u}−\mathrm{31}\right)} \\ $$$$=\frac{−{i}}{\mathrm{4}}\int\:\frac{{du}}{\left(\mathrm{3sin}^{\mathrm{2}} {u}+\mathrm{4}\sqrt{\mathrm{3}}{i}\mathrm{sin}\:{u}+\left(\mathrm{2}{i}\right)^{\mathrm{2}} \right)−\mathrm{27}} \\ $$$$=\frac{−{i}}{\mathrm{4}}\int\:\frac{{du}}{\left(\sqrt{\mathrm{3}}\mathrm{sin}\:{u}+\mathrm{2}{i}\right)^{\mathrm{2}} −\left(\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\frac{−{i}}{\mathrm{4}}\int\frac{{du}}{\left(\sqrt{\mathrm{3}}\mathrm{sin}\:{u}+\mathrm{2}{i}−\mathrm{3}\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{3}}\mathrm{sin}\:{u}+\mathrm{2}{k}+\mathrm{3}\sqrt{\mathrm{3}}\right)} \\ $$$$=\frac{−{i}}{\mathrm{4}\centerdot\mathrm{6}\sqrt{\mathrm{3}}}\left[\int\frac{{du}}{\left(\sqrt{\mathrm{3}}\mathrm{sin}\:{u}+\mathrm{2}{i}−\mathrm{3}\sqrt{\mathrm{3}}\right)}−\int\frac{{du}}{\sqrt{\mathrm{3}}\mathrm{sin}\:{u}+\mathrm{2}{i}+\mathrm{3}\sqrt{\mathrm{3}}}\right] \\ $$$$=\frac{−{i}}{\mathrm{4}\centerdot\mathrm{6}\centerdot\mathrm{3}}\left[\int\frac{{du}}{\left(\mathrm{sin}\:{u}+\left(\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{i}−\mathrm{3}\right)\right.}−\int\frac{{du}}{\mathrm{sin}\:{u}+\left(\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{i}+\mathrm{3}\right)}\right] \\ $$

Answered by prakash jain last updated on 16/Nov/15

As given in comments both integrals are of the form ∫(du/(sin u+a)) This can be integrated using the substitution tan (u/2)=v du=((2dv)/((1+v^2 ))) sin u=((2v)/(1+v^2 )) ∫(du/(sin x+a))=∫ (((2dv)/(1+v^2 ))/(((2v)/(1+v^2 ))+a))=(1/a)∫ ((2dv)/(v^2 +2(v/a)+1)) =(1/a)∫ ((2dv)/((v+(1/a))^2 +((√((√a)−(1/a^2 ))))^2 ))=tan^(−1) ...(standard integral) Fill in the required value and do a reverse substitution. You will get a long result in tan^(−1) . You can also convert the result to ln or tanh^(−1) .

$$\mathrm{As}\:\mathrm{given}\:\mathrm{in}\:\mathrm{comments}\:\mathrm{both}\:\mathrm{integrals}\:\mathrm{are} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$$\int\frac{{du}}{\mathrm{sin}\:{u}+{a}} \\ $$$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{integrated}\:\mathrm{using}\:\mathrm{the}\:\mathrm{substitution} \\ $$$$\mathrm{tan}\:\frac{{u}}{\mathrm{2}}={v} \\ $$$${du}=\frac{\mathrm{2}{dv}}{\left(\mathrm{1}+{v}^{\mathrm{2}} \right)} \\ $$$$\mathrm{sin}\:{u}=\frac{\mathrm{2}{v}}{\mathrm{1}+{v}^{\mathrm{2}} } \\ $$$$\int\frac{{du}}{\mathrm{sin}\:{x}+{a}}=\int\:\:\frac{\frac{\mathrm{2}{dv}}{\mathrm{1}+{v}^{\mathrm{2}} }}{\frac{\mathrm{2}{v}}{\mathrm{1}+{v}^{\mathrm{2}} }+{a}}=\frac{\mathrm{1}}{{a}}\int\:\frac{\mathrm{2}{dv}}{{v}^{\mathrm{2}} +\mathrm{2}\frac{{v}}{{a}}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{a}}\int\:\frac{\mathrm{2}{dv}}{\left({v}+\frac{\mathrm{1}}{{a}}\right)^{\mathrm{2}} +\left(\sqrt{\sqrt{{a}}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}\right)^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} ...\left(\mathrm{standard}\:\mathrm{integral}\right) \\ $$$$\mathrm{Fill}\:\mathrm{in}\:\mathrm{the}\:\mathrm{required}\:\mathrm{value}\:\mathrm{and}\:\mathrm{do}\:\mathrm{a}\:\mathrm{reverse} \\ $$$$\mathrm{substitution}.\:\mathrm{You}\:\mathrm{will}\:\mathrm{get}\:\mathrm{a}\:\mathrm{long}\:\mathrm{result}\:\mathrm{in}\:\mathrm{tan}^{−\mathrm{1}} . \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{also}\:\mathrm{convert}\:\mathrm{the}\:\mathrm{result}\:\mathrm{to}\:\mathrm{ln}\:\mathrm{or}\:\mathrm{tanh}^{−\mathrm{1}} . \\ $$

Commented by prakash jain last updated on 16/Nov/15

The result will contain i=(√(−1)) as well terms involving square roots of complex number.

$$\mathrm{The}\:\mathrm{result}\:\mathrm{will}\:\mathrm{contain}\:{i}=\sqrt{−\mathrm{1}}\:\mathrm{as}\:\mathrm{well}\:\mathrm{terms}\: \\ $$$$\mathrm{involving}\:\mathrm{square}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{number}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com