Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 23390 by ajfour last updated on 29/Oct/17

Commented by ajfour last updated on 31/Oct/17

(a)If released in this orientation at origin, in what time can this one spoke ring return back to origin , assuming it starts rolling on its own, and there are no net energy losses, and it doesn′t fall aside.

$$\left({a}\right){If}\:{released}\:{in}\:{this}\:{orientation} \\ $$$${at}\:{origin},\:{in}\:{what}\:{time}\:{can}\:{this} \\ $$$${one}\:{spoke}\:{ring}\:{return}\:{back}\:{to} \\ $$$${origin}\:,\:{assuming}\:{it}\:{starts}\:{rolling} \\ $$$${on}\:{its}\:{own},\:{and}\:{there}\:{are}\:{no}\:{net} \\ $$$${energy}\:{losses},\:{and}\:{it}\:{doesn}'{t}\:{fall} \\ $$$${aside}. \\ $$

Commented by ajfour last updated on 31/Oct/17

(b) Also find the angular acceleration α(θ) using Newton′s laws, that is, without using energy methods.

$$\left({b}\right)\:{Also}\:{find}\:{the}\:{angular}\:{acceleration} \\ $$$$\:\alpha\left(\theta\right)\:{using}\:{Newton}'{s}\:{laws},\:{that}\:{is}, \\ $$$${without}\:{using}\:{energy}\:{methods}. \\ $$

Answered by mrW1 last updated on 30/Oct/17

Commented by mrW1 last updated on 31/Oct/17

Point 1=COM of ring M Point 2=COM of rod (spoke) m x_1 =Rθ y_1 =R x_2 =x_1 +(R/2) sin θ=(R/2)(2θ+sin θ) y_2 =y_1 +(R/2) cos θ=(R/2)(2+cos θ) ω=(dθ/dt) v_(x1) =(dx_1 /dt)=R(dθ/dt)=Rω v_(y1) =(dy_1 /dt)=0 v_(x2) =(dx_2 /dt)=(R/2)(2+cos θ)ω v_(y2) =(dy_2 /dt)=−(R/2) sin θ ω KE_1 =(1/2)M(v_(x1) ^2 +v_(y1) ^2 )+(1/2)I_1 ω^2 =(1/2)MR^2 ω^2 +(1/2)MR^2 ω^2 =MR^2 ω^2 KE_2 =(1/2)m(v_(x2) ^2 +v_(y2) ^2 )+(1/2)I_2 ω^2 =((mR^2 ω^2 )/8)(5+4cos θ)+((mR^2 ω^2 )/(24)) =((mR^2 ω^2 )/6)(4+3cos θ) KE_1 +KE_2 =((mgR)/2)(1−cos θ) MR^2 ω^2 +((mR^2 ω^2 )/6)(4+3cos θ)=((mgR)/2)(1−cos θ) [6M+4m+3mcos θ]Rω^2 =3mg(1−cos θ) ω^2 =(g/R)×((1−cos θ)/(((6M+4m)/(3m))+cos θ))=(g/R)×((2 sin^2 (θ/2))/(((6M+4m)/(3m))+1−2sin^2 (θ/2))) ω^2 =(g/R)×((sin^2 (θ/2))/(((6M+7m)/(6m))−sin^2 (θ/2))) ω^2 =(g/R)×((sin^2 (θ/2))/(a^2 −sin^2 (θ/2))), with a^2 =((6M+7m)/(6m))=(M/m)+(7/6)>1 ⇒ω=(√(g/R))×((sin (θ/2))/(√(a^2 −sin^2 (θ/2))))=(dθ/dt) ⇒((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) dθ=(√(g/R)) dt ⇒(√(g/R))∫_0 ^( t) dt=∫_0 ^( θ) ((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) dθ ⇒t=(√(R/g))∫_0 ^( θ) ((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) dθ t=2(√(R/g))∫_0 ^( θ) ((√(a^2 −sin^2 (θ/2)))/(sin (θ/2))) d(θ/2) t=2(√(R/g))∫_0 ^( ϕ) ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ, with ϕ=(θ/2) the time which is needed for a cycle is T=2(√(R/g))∫_0 ^( π) ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ F(ϕ)=∫^ ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ =−(1/2)[a×ln ∣(((√(a^2 −sin^2 ϕ))+a ∣cos ϕ∣)/((√(a^2 −sin^2 ϕ))−a ∣cos ϕ∣))∣+ln ∣(((√(a^2 −sin^2 ϕ))−∣cos ϕ∣)/((√(a^2 −sin^2 ϕ))+∣cos ϕ∣))∣]+C =−(1/2)[a×ln ∣(((√((a^2 −1)tan^2 ϕ+a^2 ))+a)/((√((a^2 −1)tan^2 ϕ+a^2 ))−a))∣+ln ∣(((√((a^2 −1)tan^2 ϕ+a^2 ))−1)/((√((a^2 −1)tan^2 ϕ+a^2 ))+1))∣]+C ...... I can not continue due to problems with this integral at ϕ=0 and ϕ=π. what is wrong above ???

$$\mathrm{Point}\:\mathrm{1}=\mathrm{COM}\:\mathrm{of}\:\mathrm{ring}\:\mathrm{M} \\ $$$$\mathrm{Point}\:\mathrm{2}=\mathrm{COM}\:\mathrm{of}\:\mathrm{rod}\:\left(\mathrm{spoke}\right)\:\mathrm{m} \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{R}\theta \\ $$$$\mathrm{y}_{\mathrm{1}} =\mathrm{R} \\ $$$$\mathrm{x}_{\mathrm{2}} =\mathrm{x}_{\mathrm{1}} +\frac{\mathrm{R}}{\mathrm{2}}\:\mathrm{sin}\:\theta=\frac{\mathrm{R}}{\mathrm{2}}\left(\mathrm{2}\theta+\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{y}_{\mathrm{2}} =\mathrm{y}_{\mathrm{1}} +\frac{\mathrm{R}}{\mathrm{2}}\:\mathrm{cos}\:\theta=\frac{\mathrm{R}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{cos}\:\theta\right) \\ $$$$\omega=\frac{\mathrm{d}\theta}{\mathrm{dt}} \\ $$$$\mathrm{v}_{\mathrm{x1}} =\frac{\mathrm{dx}_{\mathrm{1}} }{\mathrm{dt}}=\mathrm{R}\frac{\mathrm{d}\theta}{\mathrm{dt}}=\mathrm{R}\omega \\ $$$$\mathrm{v}_{\mathrm{y1}} =\frac{\mathrm{dy}_{\mathrm{1}} }{\mathrm{dt}}=\mathrm{0} \\ $$$$\mathrm{v}_{\mathrm{x2}} =\frac{\mathrm{dx}_{\mathrm{2}} }{\mathrm{dt}}=\frac{\mathrm{R}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{cos}\:\theta\right)\omega \\ $$$$\mathrm{v}_{\mathrm{y2}} =\frac{\mathrm{dy}_{\mathrm{2}} }{\mathrm{dt}}=−\frac{\mathrm{R}}{\mathrm{2}}\:\mathrm{sin}\:\theta\:\omega \\ $$$$ \\ $$$$\mathrm{KE}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}\left(\mathrm{v}_{\mathrm{x1}} ^{\mathrm{2}} +\mathrm{v}_{\mathrm{y1}} ^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}_{\mathrm{1}} \omega^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{MR}^{\mathrm{2}} \omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{MR}^{\mathrm{2}} \omega^{\mathrm{2}} =\mathrm{MR}^{\mathrm{2}} \omega^{\mathrm{2}} \\ $$$$\mathrm{KE}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}\left(\mathrm{v}_{\mathrm{x2}} ^{\mathrm{2}} +\mathrm{v}_{\mathrm{y2}} ^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}_{\mathrm{2}} \omega^{\mathrm{2}} \\ $$$$=\frac{\mathrm{mR}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{5}+\mathrm{4cos}\:\theta\right)+\frac{\mathrm{mR}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{24}} \\ $$$$=\frac{\mathrm{mR}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{6}}\left(\mathrm{4}+\mathrm{3cos}\:\theta\right) \\ $$$$\mathrm{KE}_{\mathrm{1}} +\mathrm{KE}_{\mathrm{2}} =\frac{\mathrm{mgR}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\mathrm{MR}^{\mathrm{2}} \omega^{\mathrm{2}} +\frac{\mathrm{mR}^{\mathrm{2}} \omega^{\mathrm{2}} }{\mathrm{6}}\left(\mathrm{4}+\mathrm{3cos}\:\theta\right)=\frac{\mathrm{mgR}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\left[\mathrm{6M}+\mathrm{4m}+\mathrm{3mcos}\:\theta\right]\mathrm{R}\omega^{\mathrm{2}} =\mathrm{3mg}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{g}}{\mathrm{R}}×\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\frac{\mathrm{6M}+\mathrm{4m}}{\mathrm{3m}}+\mathrm{cos}\:\theta}=\frac{\mathrm{g}}{\mathrm{R}}×\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}{\frac{\mathrm{6M}+\mathrm{4m}}{\mathrm{3m}}+\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}} \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{g}}{\mathrm{R}}×\frac{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}{\frac{\mathrm{6M}+\mathrm{7m}}{\mathrm{6m}}−\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}} \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{g}}{\mathrm{R}}×\frac{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}},\:\mathrm{with}\:\mathrm{a}^{\mathrm{2}} =\frac{\mathrm{6M}+\mathrm{7m}}{\mathrm{6m}}=\frac{\mathrm{M}}{\mathrm{m}}+\frac{\mathrm{7}}{\mathrm{6}}>\mathrm{1} \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{g}}{\mathrm{R}}}×\frac{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}}=\frac{\mathrm{d}\theta}{\mathrm{dt}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\:\mathrm{d}\theta=\sqrt{\frac{\mathrm{g}}{\mathrm{R}}}\:\mathrm{dt} \\ $$$$\Rightarrow\sqrt{\frac{\mathrm{g}}{\mathrm{R}}}\int_{\mathrm{0}} ^{\:\mathrm{t}} \mathrm{dt}=\int_{\mathrm{0}} ^{\:\theta} \frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\:\mathrm{d}\theta \\ $$$$\Rightarrow\mathrm{t}=\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}\int_{\mathrm{0}} ^{\:\theta} \frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\:\mathrm{d}\theta \\ $$$$\mathrm{t}=\mathrm{2}\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}\int_{\mathrm{0}} ^{\:\theta} \frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}\:\mathrm{d}\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{t}=\mathrm{2}\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}\int_{\mathrm{0}} ^{\:\varphi} \frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}}{\mathrm{sin}\:\varphi}\:\mathrm{d}\varphi,\:\mathrm{with}\:\varphi=\frac{\theta}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{time}\:\mathrm{which}\:\mathrm{is}\:\mathrm{needed}\:\mathrm{for}\:\mathrm{a}\:\mathrm{cycle}\:\mathrm{is} \\ $$$$\mathrm{T}=\mathrm{2}\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}\int_{\mathrm{0}} ^{\:\pi} \frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}}{\mathrm{sin}\:\varphi}\:\mathrm{d}\varphi \\ $$$$ \\ $$$$\mathrm{F}\left(\varphi\right)=\int^{\:} \frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}}{\mathrm{sin}\:\varphi}\:\mathrm{d}\varphi \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{a}×\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}+\mathrm{a}\:\mid\mathrm{cos}\:\varphi\mid}{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}−\mathrm{a}\:\mid\mathrm{cos}\:\varphi\mid}\mid+\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}−\mid\mathrm{cos}\:\varphi\mid}{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\varphi}+\mid\mathrm{cos}\:\varphi\mid}\mid\right]+\mathrm{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{a}×\mathrm{ln}\:\mid\frac{\sqrt{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}^{\mathrm{2}} \:\varphi+\mathrm{a}^{\mathrm{2}} }+\mathrm{a}}{\sqrt{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}^{\mathrm{2}} \:\varphi+\mathrm{a}^{\mathrm{2}} }−\mathrm{a}}\mid+\mathrm{ln}\:\mid\frac{\sqrt{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}^{\mathrm{2}} \:\varphi+\mathrm{a}^{\mathrm{2}} }−\mathrm{1}}{\sqrt{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{tan}^{\mathrm{2}} \:\varphi+\mathrm{a}^{\mathrm{2}} }+\mathrm{1}}\mid\right]+\mathrm{C} \\ $$$$...... \\ $$$$\mathrm{I}\:\mathrm{can}\:\mathrm{not}\:\mathrm{continue}\:\mathrm{due}\:\mathrm{to}\:\mathrm{problems}\:\mathrm{with} \\ $$$$\mathrm{this}\:\mathrm{integral}\:\mathrm{at}\:\varphi=\mathrm{0}\:\mathrm{and}\:\varphi=\pi. \\ $$$$ \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{above}\:??? \\ $$

Commented by ajfour last updated on 31/Oct/17

take limit ϕ→0 , and ϕ→π what was the tecqnique to evaluate the Integral, Sir?

$${take}\:{limit}\:\varphi\rightarrow\mathrm{0}\:,\:{and}\:\varphi\rightarrow\pi \\ $$$${what}\:{was}\:{the}\:{tecqnique}\:{to} \\ $$$${evaluate}\:{the}\:{Integral},\:{Sir}? \\ $$

Commented by mrW1 last updated on 31/Oct/17

is there a simple solution?

$$\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{solution}? \\ $$

Commented by mrW1 last updated on 31/Oct/17

but there is no limit for ϕ→0 and π. I am simply confused.

$$\mathrm{but}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{limit}\:\mathrm{for}\:\varphi\rightarrow\mathrm{0}\:\mathrm{and}\:\pi. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{simply}\:\mathrm{confused}. \\ $$

Commented by mrW1 last updated on 31/Oct/17

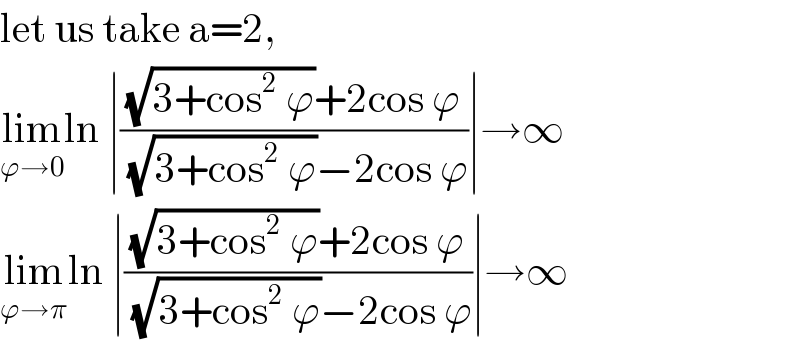
let us take a=2, lim_(ϕ→0) ln ∣(((√(3+cos^2 ϕ))+2cos ϕ)/((√(3+cos^2 ϕ))−2cos ϕ))∣→∞ lim_(ϕ→π) ln ∣(((√(3+cos^2 ϕ))+2cos ϕ)/((√(3+cos^2 ϕ))−2cos ϕ))∣→∞

$$\mathrm{let}\:\mathrm{us}\:\mathrm{take}\:\mathrm{a}=\mathrm{2}, \\ $$$$\underset{\varphi\rightarrow\mathrm{0}} {\mathrm{lim}ln}\:\mid\frac{\sqrt{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:\varphi}+\mathrm{2cos}\:\varphi}{\sqrt{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:\varphi}−\mathrm{2cos}\:\varphi}\mid\rightarrow\infty \\ $$$$\underset{\varphi\rightarrow\pi} {\mathrm{lim}ln}\:\mid\frac{\sqrt{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:\varphi}+\mathrm{2cos}\:\varphi}{\sqrt{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:\varphi}−\mathrm{2cos}\:\varphi}\mid\rightarrow\infty \\ $$

Commented by ajfour last updated on 31/Oct/17

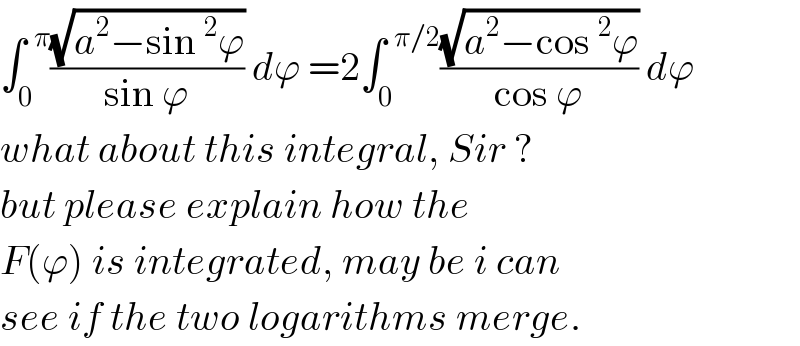
∫_0 ^( π) ((√(a^2 −sin^2 ϕ))/(sin ϕ)) dϕ =2∫_0 ^( π/2) ((√(a^2 −cos^2 ϕ))/(cos ϕ)) dϕ what about this integral, Sir ? but please explain how the F(ϕ) is integrated, may be i can see if the two logarithms merge.

$$\int_{\mathrm{0}} ^{\:\:\pi} \frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{sin}\:^{\mathrm{2}} \varphi}}{\mathrm{sin}\:\varphi}\:{d}\varphi\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{\sqrt{{a}^{\mathrm{2}} −\mathrm{cos}\:^{\mathrm{2}} \varphi}}{\mathrm{cos}\:\varphi}\:{d}\varphi \\ $$$${what}\:{about}\:{this}\:{integral},\:{Sir}\:? \\ $$$${but}\:{please}\:{explain}\:{how}\:{the} \\ $$$${F}\left(\varphi\right)\:{is}\:{integrated},\:{may}\:{be}\:{i}\:{can} \\ $$$${see}\:{if}\:{the}\:{two}\:{logarithms}\:{merge}. \\ $$

Commented by mrW1 last updated on 31/Oct/17

substitute u=tan x ⇒∫((√(a^2 +(a^2 −1)u^2 ))/(u(u^2 +1)))du substitute v=(√(a^2 +(a^2 −1)u^2 )) ⇒(a^2 −1)∫(v^2 /((v^2 −1)(v^2 −a^2 ))) dv ⇒a^2 ∫(dv/(v^2 −a^2 ))+(1/2)∫(dv/(v+1))−(1/2)∫(dv/(v−1)) =......

$$\mathrm{substitute}\:\mathrm{u}=\mathrm{tan}\:\mathrm{x} \\ $$$$\Rightarrow\int\frac{\sqrt{\mathrm{a}^{\mathrm{2}} +\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{u}^{\mathrm{2}} }}{\mathrm{u}\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{du} \\ $$$$\mathrm{substitute}\:\mathrm{v}=\sqrt{\mathrm{a}^{\mathrm{2}} +\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\int\frac{\mathrm{v}^{\mathrm{2}} }{\left(\mathrm{v}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{v}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}\:\mathrm{dv} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} \int\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dv}}{\mathrm{v}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dv}}{\mathrm{v}−\mathrm{1}} \\ $$$$=...... \\ $$

Commented by ajfour last updated on 31/Oct/17

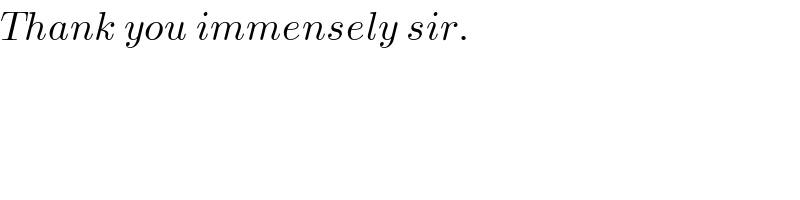
Thank you immensely sir.

$${Thank}\:{you}\:{immensely}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com