
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 23445 by tawa tawa last updated on 30/Oct/17
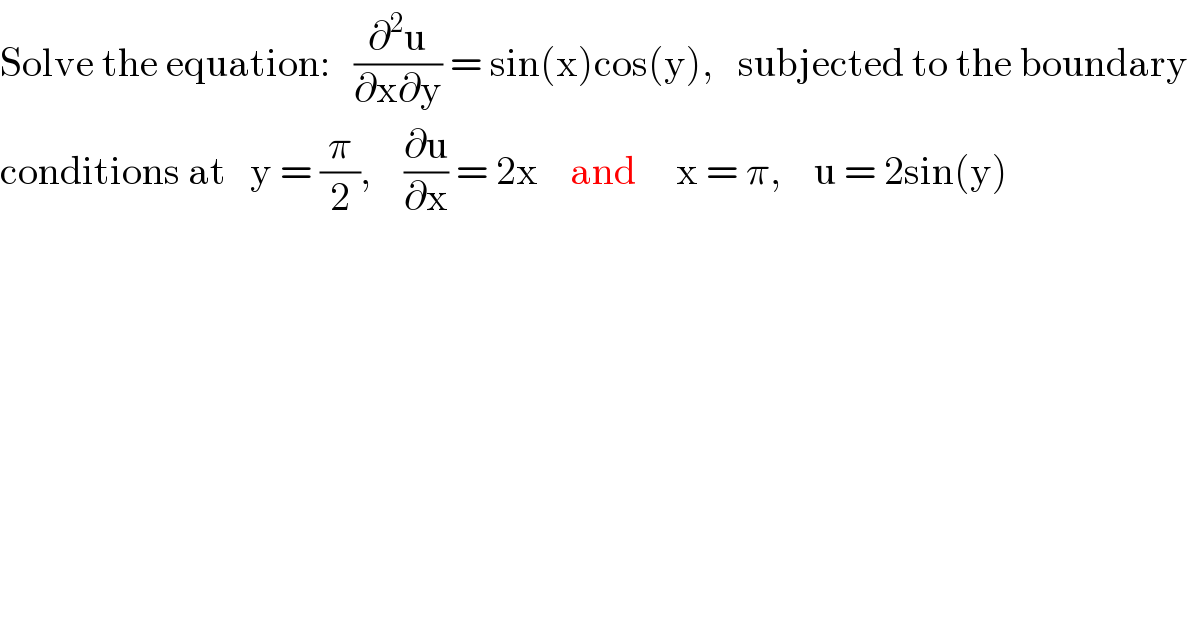
Answered by mrW1 last updated on 31/Oct/17
![(∂^2 u/(∂x∂y)) = sin(x)cos(y) ⇒(∂u/∂x)=∫sin (x) cos (y) dy=sin (x) sin (y)+f(x) sin (x) sin ((π/2))+f(x)=2x ⇒f(x)=2x−sin (x) (∂u/∂x)=sin (x) [sin (y)−1]+2x ⇒u=∫{sin (x) [sin (y)−1]+2x}dx =−cos (x)[sin (y)−1]+x^2 +C −cos (π)[sin (y)−1]+π^2 +C=2 sin (y) ⇒C= sin (y)+1−π^2 ⇒u(x,y)=cos (x)+[1−cos (x)] sin (y)+x^2 +1−π^2](Q23446.png)
Commented by tawa tawa last updated on 31/Oct/17

| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 23445 by tawa tawa last updated on 30/Oct/17 | ||
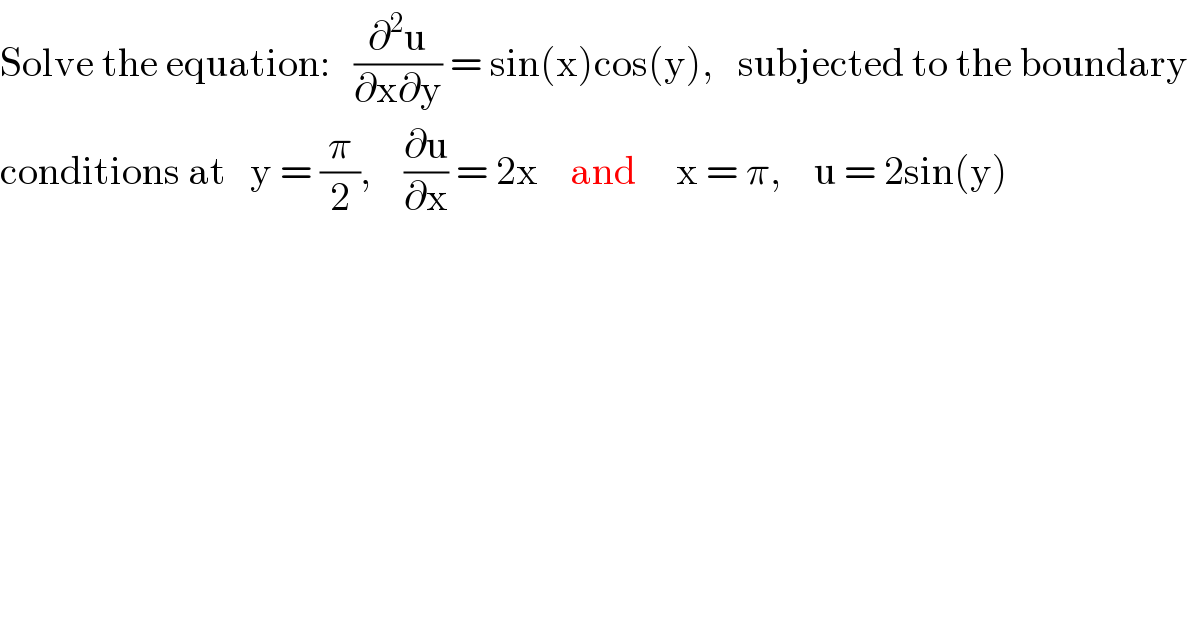 | ||
Answered by mrW1 last updated on 31/Oct/17 | ||
![(∂^2 u/(∂x∂y)) = sin(x)cos(y) ⇒(∂u/∂x)=∫sin (x) cos (y) dy=sin (x) sin (y)+f(x) sin (x) sin ((π/2))+f(x)=2x ⇒f(x)=2x−sin (x) (∂u/∂x)=sin (x) [sin (y)−1]+2x ⇒u=∫{sin (x) [sin (y)−1]+2x}dx =−cos (x)[sin (y)−1]+x^2 +C −cos (π)[sin (y)−1]+π^2 +C=2 sin (y) ⇒C= sin (y)+1−π^2 ⇒u(x,y)=cos (x)+[1−cos (x)] sin (y)+x^2 +1−π^2](Q23446.png) | ||
| ||
Commented by tawa tawa last updated on 31/Oct/17 | ||
 | ||