Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 2358 by 123456 last updated on 18/Nov/15

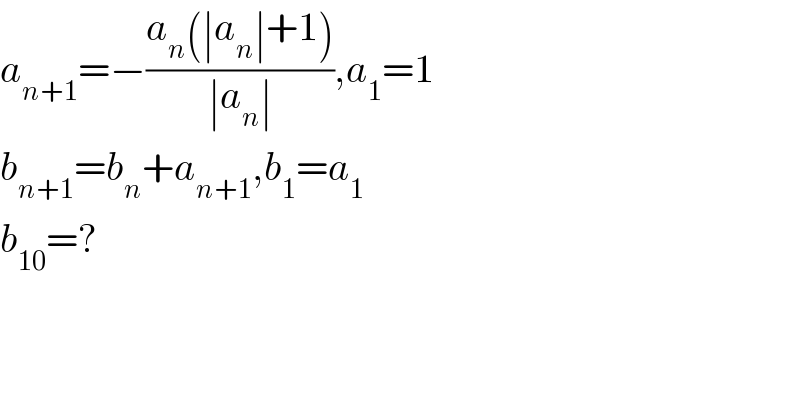
a_(n+1) =−((a_n (∣a_n ∣+1))/(∣a_n ∣)),a_1 =1 b_(n+1) =b_n +a_(n+1) ,b_1 =a_1 b_(10) =?

$${a}_{{n}+\mathrm{1}} =−\frac{{a}_{{n}} \left(\mid{a}_{{n}} \mid+\mathrm{1}\right)}{\mid{a}_{{n}} \mid},{a}_{\mathrm{1}} =\mathrm{1} \\ $$$${b}_{{n}+\mathrm{1}} ={b}_{{n}} +{a}_{{n}+\mathrm{1}} ,{b}_{\mathrm{1}} ={a}_{\mathrm{1}} \\ $$$${b}_{\mathrm{10}} =? \\ $$

Answered by Filup last updated on 18/Nov/15

continued (without working) (working is simple) a_1 =1 b_1 =1 a_2 =−2 b_2 =−1 a_3 =3 b_3 =2 a_4 =−4 b_4 =−2 a_5 =5 b_5 =3 a_6 =−6 b_6 =−3 a_7 =7 b_7 =4 a_8 =−8 b_8 =−4 a_9 =9 b_9 =5 a_(10) =−10 b_(10) =−5 ∴b_(10) =−5

$${continued}\:\left(\mathrm{without}\:\mathrm{working}\right) \\ $$$$\left(\mathrm{working}\:\mathrm{is}\:\mathrm{simple}\right) \\ $$$${a}_{\mathrm{1}} =\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:{b}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{\mathrm{2}} =−\mathrm{2}\:\:\:\:\:\:\:\:{b}_{\mathrm{2}} =−\mathrm{1} \\ $$$${a}_{\mathrm{3}} =\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:{b}_{\mathrm{3}} =\mathrm{2} \\ $$$${a}_{\mathrm{4}} =−\mathrm{4}\:\:\:\:\:\:\:\:{b}_{\mathrm{4}} =−\mathrm{2} \\ $$$${a}_{\mathrm{5}} =\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:{b}_{\mathrm{5}} =\mathrm{3} \\ $$$${a}_{\mathrm{6}} =−\mathrm{6}\:\:\:\:\:\:\:\:{b}_{\mathrm{6}} =−\mathrm{3} \\ $$$${a}_{\mathrm{7}} =\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:{b}_{\mathrm{7}} =\mathrm{4} \\ $$$${a}_{\mathrm{8}} =−\mathrm{8}\:\:\:\:\:\:\:\:{b}_{\mathrm{8}} =−\mathrm{4} \\ $$$${a}_{\mathrm{9}} =\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:{b}_{\mathrm{9}} =\mathrm{5} \\ $$$${a}_{\mathrm{10}} =−\mathrm{10}\:\:\:\:{b}_{\mathrm{10}} =−\mathrm{5} \\ $$$$ \\ $$$$\therefore{b}_{\mathrm{10}} =−\mathrm{5} \\ $$

Commented by Filup last updated on 18/Nov/15

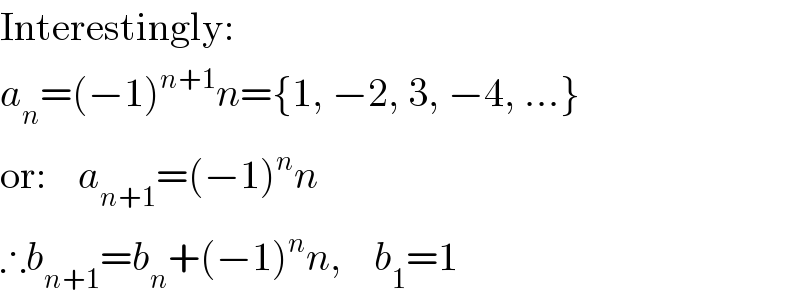
Interestingly: a_n =(−1)^(n+1) n={1, −2, 3, −4, ...} or: a_(n+1) =(−1)^n n ∴b_(n+1) =b_n +(−1)^n n, b_1 =1

$$\mathrm{Interestingly}: \\ $$$${a}_{{n}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}=\left\{\mathrm{1},\:−\mathrm{2},\:\mathrm{3},\:−\mathrm{4},\:...\right\} \\ $$$$\mathrm{or}:\:\:\:\:{a}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}} {n} \\ $$$$\therefore{b}_{{n}+\mathrm{1}} ={b}_{{n}} +\left(−\mathrm{1}\right)^{{n}} {n},\:\:\:\:{b}_{\mathrm{1}} =\mathrm{1} \\ $$

Commented by Filup last updated on 18/Nov/15

a_(n+1) =−((a_n (a_n +1))/(∣a_n ∣)), (a_1 =1) a_(n+1) =−sgn(a_n )(a_n +1) a_(n+1) =sgn(−a_n )(a_n +1) ∴ if a_k =+ve, a_(k+1) =−ve Now, knowing the sequence gives: 1, −2, 3, −4, ... We can evaluate that: a_(n+1) =(−1)^n n ∴a_(n+1) =(−1)^n n=sgn(−a_n )(a_n +1) Thought that was interesting as it is able to show any a_(n+1) when given a_n . Or the other way around e.g. a_(10) =−10 ∴−10=sgn(−a_9 )(a_9 +1) ∵a_(n+1) =sgn(−a_9 )a_9 ±a_(n+1) =∓a_n ↓ RHS shows that if a_k =+ve, a_(k±1) =−ve ∴−10=sgn(−a_9 )(a_9 +1) ∴−10=−sgn(a_9 )(a_9 +1) LHS=−ve, ∴RHS=+ve sgn(x)=±1→sgn(a_9 )=+ve ∴−10=−(+(a_9 +1)) ∴−10=−a_9 −1 ∴10=a_9 +1 ∴a_9 =9 Which is true from above

$${a}_{{n}+\mathrm{1}} =−\frac{{a}_{{n}} \left({a}_{{n}} +\mathrm{1}\right)}{\mid{a}_{{n}} \mid},\:\:\:\left({a}_{\mathrm{1}} =\mathrm{1}\right) \\ $$$${a}_{{n}+\mathrm{1}} =−\mathrm{sgn}\left({a}_{{n}} \right)\left({a}_{{n}} +\mathrm{1}\right) \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{sgn}\left(−{a}_{{n}} \right)\left({a}_{{n}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\therefore\:\mathrm{if}\:{a}_{{k}} =+\mathrm{ve},\:\:\:\:\:\:{a}_{{k}+\mathrm{1}} =−\mathrm{ve} \\ $$$$\mathrm{Now},\:\mathrm{knowing}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{gives}: \\ $$$$\mathrm{1},\:−\mathrm{2},\:\mathrm{3},\:−\mathrm{4},\:... \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{evaluate}\:\mathrm{that}: \\ $$$${a}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}} {n} \\ $$$$\therefore{a}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}} {n}=\mathrm{sgn}\left(−{a}_{{n}} \right)\left({a}_{{n}} +\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{Thought}\:\mathrm{that}\:\mathrm{was}\:\mathrm{interesting}\:\mathrm{as}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{able}\:\mathrm{to}\:\mathrm{show}\:\mathrm{any}\:{a}_{{n}+\mathrm{1}} \:\mathrm{when}\:\mathrm{given}\:{a}_{{n}} .\: \\ $$$${Or}\:{the}\:{other}\:{way}\:{around} \\ $$$$ \\ $$$$\mathrm{e}.\mathrm{g}.\:\:\:\:{a}_{\mathrm{10}} =−\mathrm{10} \\ $$$$\therefore−\mathrm{10}=\mathrm{sgn}\left(−{a}_{\mathrm{9}} \right)\left({a}_{\mathrm{9}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because{a}_{{n}+\mathrm{1}} =\mathrm{sgn}\left(−{a}_{\mathrm{9}} \right){a}_{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\pm{a}_{{n}+\mathrm{1}} =\mp{a}_{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\downarrow \\ $$$$\mathrm{RHS}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{if}\:{a}_{{k}} =+\mathrm{ve},\:\:{a}_{{k}\pm\mathrm{1}} =−\mathrm{ve} \\ $$$$\therefore−\mathrm{10}=\mathrm{sgn}\left(−{a}_{\mathrm{9}} \right)\left({a}_{\mathrm{9}} +\mathrm{1}\right) \\ $$$$\therefore−\mathrm{10}=−\mathrm{sgn}\left({a}_{\mathrm{9}} \right)\left({a}_{\mathrm{9}} +\mathrm{1}\right) \\ $$$$\mathrm{LHS}=−\mathrm{ve},\:\:\:\therefore\mathrm{RHS}=+\mathrm{ve} \\ $$$$\mathrm{sgn}\left({x}\right)=\pm\mathrm{1}\rightarrow\mathrm{sgn}\left({a}_{\mathrm{9}} \right)=+\mathrm{ve} \\ $$$$\therefore−\mathrm{10}=−\left(+\left({a}_{\mathrm{9}} +\mathrm{1}\right)\right) \\ $$$$\therefore−\mathrm{10}=−{a}_{\mathrm{9}} −\mathrm{1} \\ $$$$\therefore\mathrm{10}={a}_{\mathrm{9}} +\mathrm{1} \\ $$$$\therefore{a}_{\mathrm{9}} =\mathrm{9} \\ $$$$\mathrm{Which}\:\mathrm{is}\:\mathrm{true}\:\mathrm{from}\:\mathrm{above} \\ $$

Commented by RasheedAhmad last updated on 18/Nov/15

G_(OO) D Discovery!

$$\mathcal{G}_{\mathcal{OO}} \mathcal{D}\:\mathcal{D}{iscovery}! \\ $$

Answered by Filup last updated on 18/Nov/15

a_(n+1) =−a_n (1+(1/(∣a_n ∣))) a_(n+1) =−a_n −(a_n /(∣a_n ∣)) (a_n /(∣a_n ∣))= { ((1 if a_n >0)),((−1 if a_n <0)) :} =sgn(a_n ) if a_n =0, (a_n /(∣a_n ∣))=undefined −sgn(x)=sgn(−x) a_(n+1) =−(a_n +sgn(a_n )) a_(n+1) =sgn(−a_n )−a_n ∴b_(n+1) =b_n +sgn(−a_n )−a_n continue

$${a}_{{n}+\mathrm{1}} =−{a}_{{n}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mid{a}_{{n}} \mid}\right) \\ $$$${a}_{{n}+\mathrm{1}} =−{a}_{{n}} −\frac{{a}_{{n}} }{\mid{a}_{{n}} \mid} \\ $$$$\frac{{a}_{{n}} }{\mid{a}_{{n}} \mid}=\begin{cases}{\mathrm{1}\:\:\:\:\:\mathrm{if}\:{a}_{{n}} >\mathrm{0}}\\{−\mathrm{1}\:\mathrm{if}\:{a}_{{n}} <\mathrm{0}}\end{cases}\:=\mathrm{sgn}\left({a}_{{n}} \right) \\ $$$$\mathrm{if}\:{a}_{{n}} =\mathrm{0},\:\frac{{a}_{{n}} }{\mid{a}_{{n}} \mid}=\mathrm{undefined} \\ $$$$ \\ $$$$−\mathrm{sgn}\left({x}\right)=\mathrm{sgn}\left(−{x}\right) \\ $$$${a}_{{n}+\mathrm{1}} =−\left({a}_{{n}} +\mathrm{sgn}\left({a}_{{n}} \right)\right) \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{sgn}\left(−{a}_{{n}} \right)−{a}_{{n}} \\ $$$$ \\ $$$$\therefore{b}_{{n}+\mathrm{1}} ={b}_{{n}} +\mathrm{sgn}\left(−{a}_{{n}} \right)−{a}_{{n}} \\ $$$$ \\ $$$$\mathrm{continue} \\ $$

Commented by Filup last updated on 18/Nov/15

only way i can tell to solve for b_(10) is to solve a_2 , a_3 , ..., a_(10) and plugging them into b. I′m lazy so i havent done it. If this goes unanswered, i will do it.

$$\mathrm{only}\:\mathrm{way}\:\mathrm{i}\:\mathrm{can}\:\mathrm{tell}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:{b}_{\mathrm{10}} \:\mathrm{is}\:\mathrm{to} \\ $$$$\mathrm{solve}\:{a}_{\mathrm{2}} ,\:{a}_{\mathrm{3}} ,\:...,\:{a}_{\mathrm{10}} \:\mathrm{and}\:\mathrm{plugging}\:\mathrm{them} \\ $$$$\mathrm{into}\:{b}.\:\mathrm{I}'\mathrm{m}\:\mathrm{lazy}\:\mathrm{so}\:\mathrm{i}\:\mathrm{havent}\:\mathrm{done}\:\mathrm{it}.\:\mathrm{If} \\ $$$$\mathrm{this}\:\mathrm{goes}\:\mathrm{unanswered},\:\mathrm{i}\:\mathrm{will}\:\mathrm{do}\:\mathrm{it}. \\ $$

Commented by RasheedAhmad last updated on 18/Nov/15

Like your approach! −−−−−−−−−−−− There is a mistake(which however doesn′t affect your logic allover). (a_n /(∣a_n ∣))= { ((1 if a_n >0)),((0 if a_n =0_(−) )),((−1 if a_n <0)) :} If a_n =0, (a_n /(∣a_n ∣)) is undefined.

$${Like}\:{your}\:{approach}! \\ $$$$−−−−−−−−−−−− \\ $$$$\:{There}\:{is}\:{a}\:{mistake}\left({which}\:{however}\right. \\ $$$$\left.{doesn}'{t}\:{affect}\:{your}\:{logic}\:{allover}\right). \\ $$$$\frac{{a}_{{n}} }{\mid{a}_{{n}} \mid}=\begin{cases}{\mathrm{1}\:\:\:\:\:\mathrm{if}\:{a}_{{n}} >\mathrm{0}}\\{\underset{−} {\mathrm{0}\:\:\:\:\:\mathrm{if}\:{a}_{{n}} =\mathrm{0}}}\\{−\mathrm{1}\:\mathrm{if}\:{a}_{{n}} <\mathrm{0}}\end{cases} \\ $$$${If}\:{a}_{{n}} =\mathrm{0},\:\frac{{a}_{{n}} }{\mid{a}_{{n}} \mid}\:{is}\:{undefined}. \\ $$

Commented by Filup last updated on 18/Nov/15

Thank You <3

$$\mathcal{T}{hank}\:\mathcal{Y}{ou}\:<\mathrm{3} \\ $$

Commented by Filup last updated on 18/Nov/15

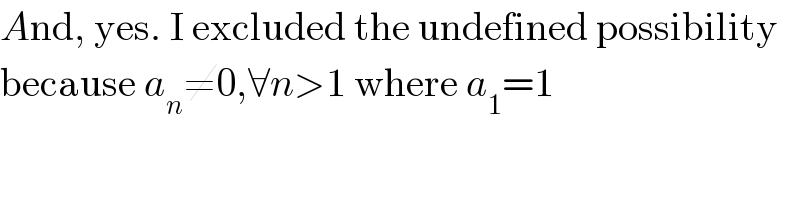
And, yes. I excluded the undefined possibility because a_n ≠0,∀n>1 where a_1 =1

$${A}\mathrm{nd},\:\mathrm{yes}.\:\mathrm{I}\:\mathrm{excluded}\:\mathrm{the}\:\mathrm{undefined}\:\mathrm{possibility} \\ $$$$\mathrm{because}\:{a}_{{n}} \neq\mathrm{0},\forall{n}>\mathrm{1}\:\mathrm{where}\:{a}_{\mathrm{1}} =\mathrm{1} \\ $$

Answered by RasheedAhmad last updated on 18/Nov/15

Trying a different approach a_(n+1) =−((a_n (∣a_n ∣+1))/(∣a_n ∣)),a_1 =1 b_(n+1) =b_n +a_(n+1) ,b_1 =a_1 b_(10) =? −−−−−−−−−− Case−I : When a_n >0⇒∣a_n ∣=a_n a_(n+1) =−((a_n (∣a_n ∣+1))/(∣a_n ∣)) ⇒ a_(n+1) =−((a_n (a_n +1))/a_n )=−(a_n +1) { (( a_(n+1) =−(a_n +1))),((b_(n+1) =b_n −(a_n +1))) :} Case−II :When a_n =0⇒∣a_n ∣=a_n =0 a_(n+1) is undefined in this case which means if any of a_n is 0 all the next a_n ′s will be undefined. Case−III:When a_n <0⇒∣a_n ∣=−a_n a_(n+1) =−((a_n (−a_n +1))/(−a_n ))=−a_n +1 { ((a_(n+1) =−a_n +1)),((b_(n+1) =b_n −a_n +1)) :} −−−−−−−−−−−−−−− { (( { (( a_(n+1) =−(a_n +1))),((b_(n+1) =b_n −(a_n +1))) :} when a_n >0 )),((a_(n+1) is undefined when a_n =0)),(( { ((a_(n+1) =−a_n +1)),((b_(n+1) =b_n −a_n +1)) :} when a_n <0)) :} Since a_1 =1>0, for a_2 Case−I is applied. The remaining process of mine is similar to that of Mr. Filup.

$${Trying}\:{a}\:{different}\:{approach} \\ $$$${a}_{{n}+\mathrm{1}} =−\frac{{a}_{{n}} \left(\mid{a}_{{n}} \mid+\mathrm{1}\right)}{\mid{a}_{{n}} \mid},{a}_{\mathrm{1}} =\mathrm{1} \\ $$$${b}_{{n}+\mathrm{1}} ={b}_{{n}} +{a}_{{n}+\mathrm{1}} ,{b}_{\mathrm{1}} ={a}_{\mathrm{1}} \\ $$$${b}_{\mathrm{10}} =? \\ $$$$−−−−−−−−−− \\ $$$${Case}−{I}\::\:{When}\:\:{a}_{{n}} >\mathrm{0}\Rightarrow\mid{a}_{{n}} \mid={a}_{{n}} \\ $$$${a}_{{n}+\mathrm{1}} =−\frac{{a}_{{n}} \left(\mid{a}_{{n}} \mid+\mathrm{1}\right)}{\mid{a}_{{n}} \mid} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:{a}_{{n}+\mathrm{1}} =−\frac{{a}_{{n}} \left({a}_{{n}} +\mathrm{1}\right)}{{a}_{{n}} }=−\left({a}_{{n}} +\mathrm{1}\right) \\ $$$$\begin{cases}{\:{a}_{{n}+\mathrm{1}} =−\left({a}_{{n}} +\mathrm{1}\right)}\\{{b}_{{n}+\mathrm{1}} ={b}_{{n}} −\left({a}_{{n}} +\mathrm{1}\right)}\end{cases} \\ $$$${Case}−{II}\::{When}\:{a}_{{n}} =\mathrm{0}\Rightarrow\mid{a}_{{n}} \mid={a}_{{n}} =\mathrm{0} \\ $$$${a}_{{n}+\mathrm{1}} \:\:{is}\:{undefined}\:{in}\:{this}\:{case} \\ $$$${which}\:{means}\:{if}\:{any}\:{of}\:{a}_{{n}} \:{is}\:\mathrm{0} \\ $$$${all}\:{the}\:{next}\:{a}_{{n}} '{s}\:{will}\:{be}\:{undefined}. \\ $$$${Case}−{III}:{When}\:{a}_{{n}} <\mathrm{0}\Rightarrow\mid{a}_{{n}} \mid=−{a}_{{n}} \:\:\:\:\:\:\: \\ $$$${a}_{{n}+\mathrm{1}} =−\frac{{a}_{{n}} \left(−{a}_{{n}} +\mathrm{1}\right)}{−{a}_{{n}} }=−{a}_{{n}} +\mathrm{1} \\ $$$$\begin{cases}{{a}_{{n}+\mathrm{1}} =−{a}_{{n}} +\mathrm{1}}\\{{b}_{{n}+\mathrm{1}} ={b}_{{n}} −{a}_{{n}} +\mathrm{1}}\end{cases} \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\begin{cases}{\begin{cases}{\:{a}_{{n}+\mathrm{1}} =−\left({a}_{{n}} +\mathrm{1}\right)}\\{{b}_{{n}+\mathrm{1}} ={b}_{{n}} −\left({a}_{{n}} +\mathrm{1}\right)}\end{cases}\:{when}\:{a}_{{n}} >\mathrm{0}\:}\\{{a}_{{n}+\mathrm{1}} \:{is}\:{undefined}\:\:\:{when}\:{a}_{{n}} =\mathrm{0}}\\{\begin{cases}{{a}_{{n}+\mathrm{1}} =−{a}_{{n}} +\mathrm{1}}\\{{b}_{{n}+\mathrm{1}} ={b}_{{n}} −{a}_{{n}} +\mathrm{1}}\end{cases}\:\:\:\:{when}\:{a}_{{n}} <\mathrm{0}}\end{cases} \\ $$$${Since}\:{a}_{\mathrm{1}} =\mathrm{1}>\mathrm{0},\:{for}\:{a}_{\mathrm{2}} \:{Case}−{I}\:{is}\: \\ $$$${applied}. \\ $$$${The}\:{remaining}\:{process}\:{of}\:{mine} \\ $$$${is}\:{similar}\:{to}\:{that}\:{of}\:{Mr}.\:{Filup}. \\ $$$$ \\ $$

Commented by Filup last updated on 18/Nov/15

I didn′t even think about evaluating a_n the way you did. Nice work!

$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{even}\:\mathrm{think}\:\mathrm{about}\:\mathrm{evaluating} \\ $$$${a}_{{n}} \:\mathrm{the}\:\mathrm{way}\:\mathrm{you}\:\mathrm{did}.\:\mathrm{Nice}\:\mathrm{work}! \\ $$

Commented by RasheedAhmad last updated on 19/Nov/15

THANK^S

$$\mathcal{THANK}^{\mathcal{S}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com