Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 23592 by Tinkutara last updated on 02/Nov/17

Let ABC be a triangle with AB = AC and ∠BAC = 30°. Let A′ be the reflection of A in the line BC; B′ be the reflection of B in the line CA; C′ be the reflection of C in the line AB. Show that A′, B′, C′ form the vertices of an equilateral triangle.

$$\mathrm{Let}\:{ABC}\:\mathrm{be}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with}\:{AB}\:=\:{AC} \\ $$$$\mathrm{and}\:\angle{BAC}\:=\:\mathrm{30}°.\:\mathrm{Let}\:{A}'\:\mathrm{be}\:\mathrm{the}\:\mathrm{reflection} \\ $$$$\mathrm{of}\:{A}\:\mathrm{in}\:\mathrm{the}\:\mathrm{line}\:{BC};\:{B}'\:\mathrm{be}\:\mathrm{the}\:\mathrm{reflection} \\ $$$$\mathrm{of}\:{B}\:\mathrm{in}\:\mathrm{the}\:\mathrm{line}\:{CA};\:{C}'\:\mathrm{be}\:\mathrm{the}\:\mathrm{reflection} \\ $$$$\mathrm{of}\:{C}\:\mathrm{in}\:\mathrm{the}\:\mathrm{line}\:{AB}.\:\mathrm{Show}\:\mathrm{that}\:{A}',\:{B}',\:{C}' \\ $$$$\mathrm{form}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{an}\:\mathrm{equilateral} \\ $$$$\mathrm{triangle}. \\ $$

Answered by ajfour last updated on 02/Nov/17

Commented by Tinkutara last updated on 06/Nov/17

Commented by Tinkutara last updated on 06/Nov/17

Commented by ajfour last updated on 02/Nov/17

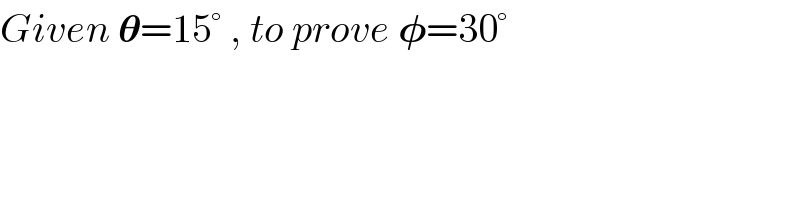
Given 𝛉=15° , to prove 𝛗=30°

$${Given}\:\boldsymbol{\theta}=\mathrm{15}°\:,\:{to}\:{prove}\:\boldsymbol{\phi}=\mathrm{30}° \\ $$

Commented by ajfour last updated on 02/Nov/17

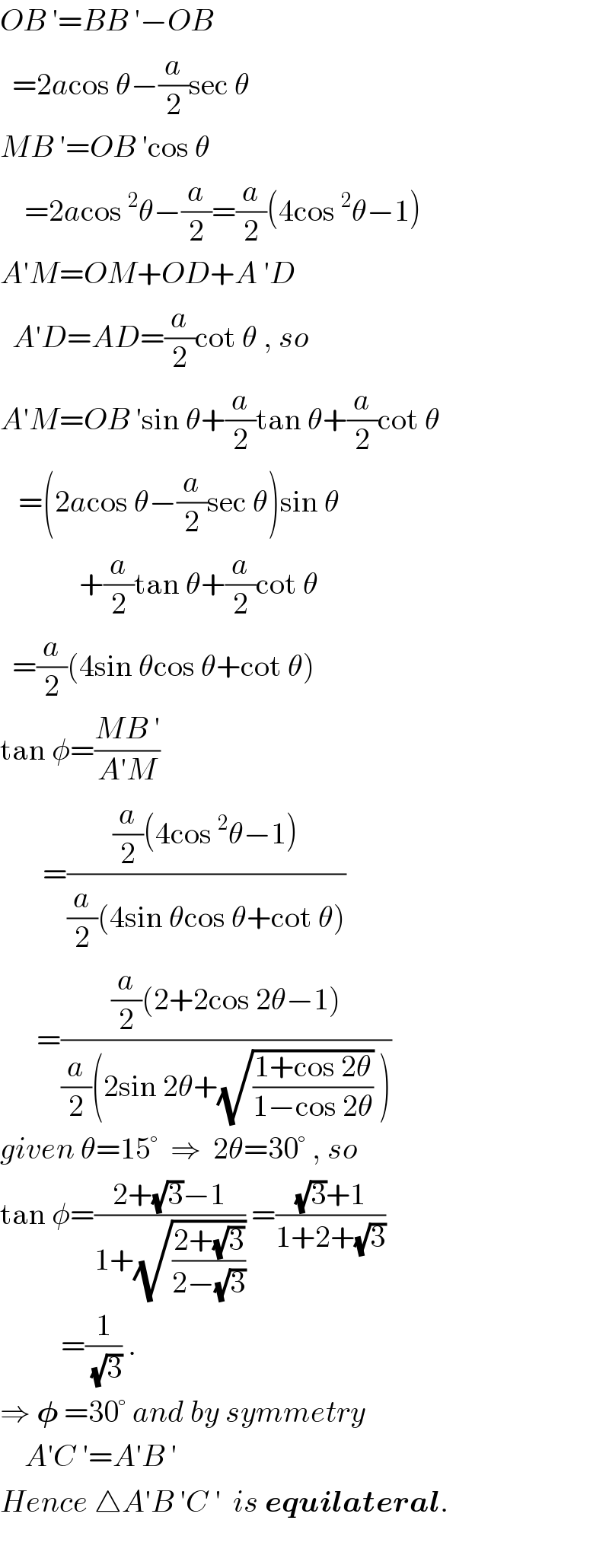
OB ′=BB ′−OB =2acos θ−(a/2)sec θ MB ′=OB ′cos θ =2acos^2 θ−(a/2)=(a/2)(4cos^2 θ−1) A′M=OM+OD+A ′D A′D=AD=(a/2)cot θ , so A′M=OB ′sin θ+(a/2)tan θ+(a/2)cot θ =(2acos θ−(a/2)sec θ)sin θ +(a/2)tan θ+(a/2)cot θ =(a/2)(4sin θcos θ+cot θ) tan φ=((MB ′)/(A′M)) =(((a/2)(4cos^2 θ−1))/((a/2)(4sin θcos θ+cot θ))) =(((a/2)(2+2cos 2θ−1))/((a/2)(2sin 2θ+(√((1+cos 2θ)/(1−cos 2θ))) ))) given θ=15° ⇒ 2θ=30° , so tan φ=((2+(√3)−1)/(1+(√((2+(√3))/(2−(√3)))))) =(((√3)+1)/(1+2+(√3))) =(1/(√3)) . ⇒ 𝛗 =30° and by symmetry A′C ′=A′B ′ Hence △A′B ′C ′ is equilateral.

$${OB}\:'={BB}\:'−{OB} \\ $$$$\:\:=\mathrm{2}{a}\mathrm{cos}\:\theta−\frac{{a}}{\mathrm{2}}\mathrm{sec}\:\theta \\ $$$${MB}\:'={OB}\:'\mathrm{cos}\:\theta \\ $$$$\:\:\:\:=\mathrm{2}{a}\mathrm{cos}\:^{\mathrm{2}} \theta−\frac{{a}}{\mathrm{2}}=\frac{{a}}{\mathrm{2}}\left(\mathrm{4cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right) \\ $$$${A}'{M}={OM}+{OD}+{A}\:'{D} \\ $$$$\:\:{A}'{D}={AD}=\frac{{a}}{\mathrm{2}}\mathrm{cot}\:\theta\:,\:{so} \\ $$$${A}'{M}={OB}\:'\mathrm{sin}\:\theta+\frac{{a}}{\mathrm{2}}\mathrm{tan}\:\theta+\frac{{a}}{\mathrm{2}}\mathrm{cot}\:\theta \\ $$$$\:\:\:=\left(\mathrm{2}{a}\mathrm{cos}\:\theta−\frac{{a}}{\mathrm{2}}\mathrm{sec}\:\theta\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{a}}{\mathrm{2}}\mathrm{tan}\:\theta+\frac{{a}}{\mathrm{2}}\mathrm{cot}\:\theta \\ $$$$\:\:=\frac{{a}}{\mathrm{2}}\left(\mathrm{4sin}\:\theta\mathrm{cos}\:\theta+\mathrm{cot}\:\theta\right) \\ $$$$\mathrm{tan}\:\phi=\frac{{MB}\:'}{{A}'{M}} \\ $$$$\:\:\:\:\:\:\:=\frac{\frac{{a}}{\mathrm{2}}\left(\mathrm{4cos}\:^{\mathrm{2}} \theta−\mathrm{1}\right)}{\frac{{a}}{\mathrm{2}}\left(\mathrm{4sin}\:\theta\mathrm{cos}\:\theta+\mathrm{cot}\:\theta\right)} \\ $$$$\:\:\:\:\:\:=\frac{\frac{{a}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{2cos}\:\mathrm{2}\theta−\mathrm{1}\right)}{\frac{{a}}{\mathrm{2}}\left(\mathrm{2sin}\:\mathrm{2}\theta+\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}}\:\right)} \\ $$$${given}\:\theta=\mathrm{15}°\:\:\Rightarrow\:\:\mathrm{2}\theta=\mathrm{30}°\:,\:{so} \\ $$$$\mathrm{tan}\:\phi=\frac{\mathrm{2}+\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{1}+\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}}}}\:=\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{1}+\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:. \\ $$$$\Rightarrow\:\boldsymbol{\phi}\:=\mathrm{30}°\:{and}\:{by}\:{symmetry} \\ $$$$\:\:\:\:{A}'{C}\:'={A}'{B}\:' \\ $$$${Hence}\:\bigtriangleup{A}'{B}\:'{C}\:'\:\:{is}\:\boldsymbol{{equilateral}}. \\ $$$$\:\:\: \\ $$

Commented by Tinkutara last updated on 02/Nov/17

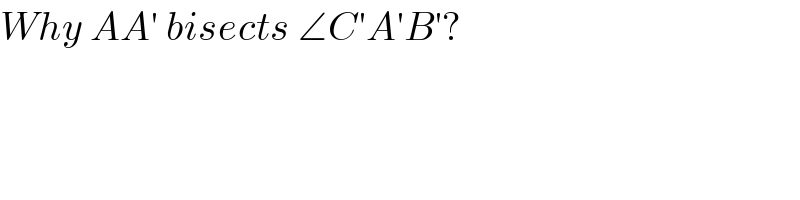
Why AA′ bisects ∠C′A′B′?

$${Why}\:{AA}'\:{bisects}\:\angle{C}'{A}'{B}'? \\ $$

Commented by ajfour last updated on 02/Nov/17

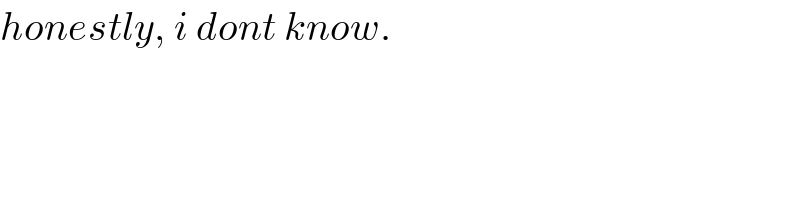
honestly, i dont know.

$${honestly},\:{i}\:{dont}\:{know}. \\ $$

Commented by Tinkutara last updated on 06/Nov/17

Commented by ajfour last updated on 06/Nov/17

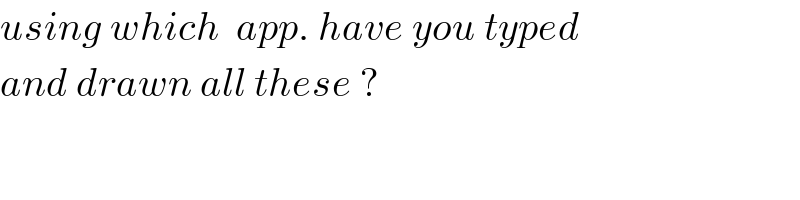
using which app. have you typed and drawn all these ?

$${using}\:{which}\:\:{app}.\:{have}\:{you}\:{typed} \\ $$$${and}\:{drawn}\:{all}\:{these}\:?\: \\ $$

Commented by Tinkutara last updated on 15/Nov/17

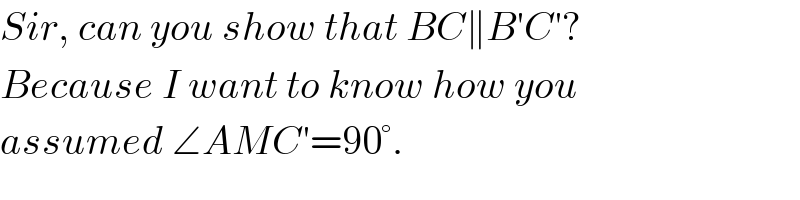
Sir, can you show that BC∥B′C′? Because I want to know how you assumed ∠AMC′=90°.

$${Sir},\:{can}\:{you}\:{show}\:{that}\:{BC}\parallel{B}'{C}'? \\ $$$${Because}\:{I}\:{want}\:{to}\:{know}\:{how}\:{you} \\ $$$${assumed}\:\angle{AMC}'=\mathrm{90}°. \\ $$

Commented by ajfour last updated on 15/Nov/17

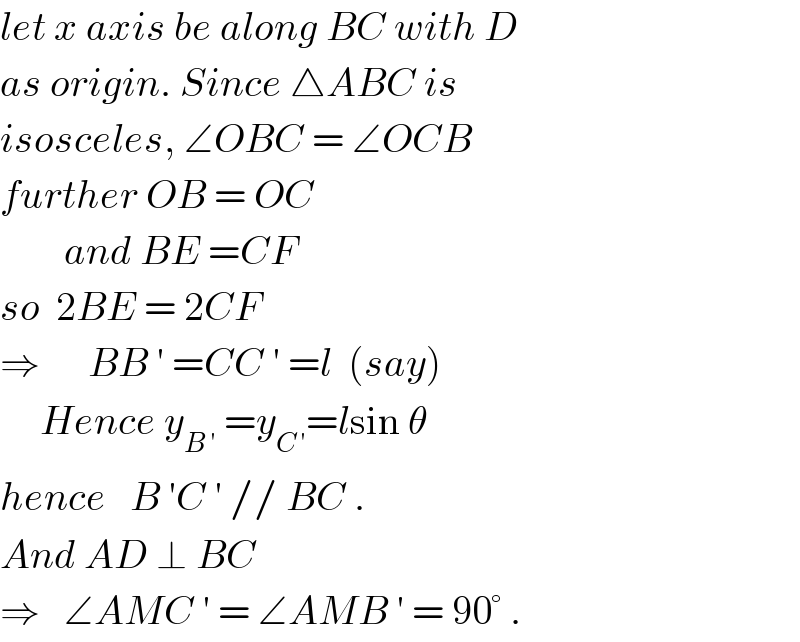
let x axis be along BC with D as origin. Since △ABC is isosceles, ∠OBC = ∠OCB further OB = OC and BE =CF so 2BE = 2CF ⇒ BB ′ =CC ′ =l (say) Hence y_(B ′) =y_(C ′) =lsin θ hence B ′C ′ // BC . And AD ⊥ BC ⇒ ∠AMC ′ = ∠AMB ′ = 90° .

$${let}\:{x}\:{axis}\:{be}\:{along}\:{BC}\:{with}\:{D} \\ $$$${as}\:{origin}.\:{Since}\:\bigtriangleup{ABC}\:{is} \\ $$$${isosceles},\:\angle{OBC}\:=\:\angle{OCB} \\ $$$${further}\:{OB}\:=\:{OC} \\ $$$$\:\:\:\:\:\:\:\:{and}\:{BE}\:={CF} \\ $$$${so}\:\:\mathrm{2}{BE}\:=\:\mathrm{2}{CF} \\ $$$$\Rightarrow\:\:\:\:\:\:{BB}\:'\:={CC}\:'\:={l}\:\:\left({say}\right) \\ $$$$\:\:\:\:\:{Hence}\:{y}_{{B}\:'} \:={y}_{{C}\:'} ={l}\mathrm{sin}\:\theta \\ $$$${hence}\:\:\:{B}\:'{C}\:'\://\:{BC}\:. \\ $$$${And}\:{AD}\:\bot\:{BC}\: \\ $$$$\Rightarrow\:\:\:\angle{AMC}\:'\:=\:\angle{AMB}\:'\:=\:\mathrm{90}°\:. \\ $$

Commented by Tinkutara last updated on 15/Nov/17

What is y_(B′) ?

$${What}\:{is}\:{y}_{{B}'} ? \\ $$

Commented by ajfour last updated on 15/Nov/17

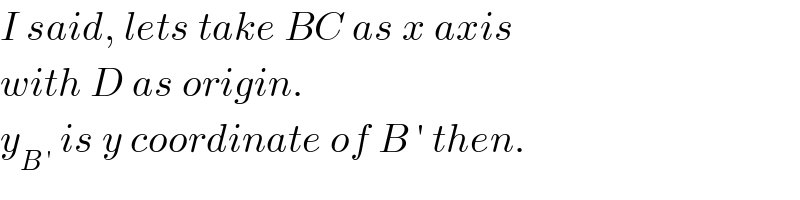
I said, lets take BC as x axis with D as origin. y_(B ′) is y coordinate of B ′ then.

$${I}\:{said},\:{lets}\:{take}\:{BC}\:{as}\:{x}\:{axis} \\ $$$${with}\:{D}\:{as}\:{origin}. \\ $$$${y}_{{B}\:'} \:{is}\:{y}\:{coordinate}\:{of}\:{B}\:'\:{then}. \\ $$

Commented by Tinkutara last updated on 15/Nov/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com