Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 23632 by ajfour last updated on 02/Nov/17

Commented by mrW1 last updated on 03/Nov/17

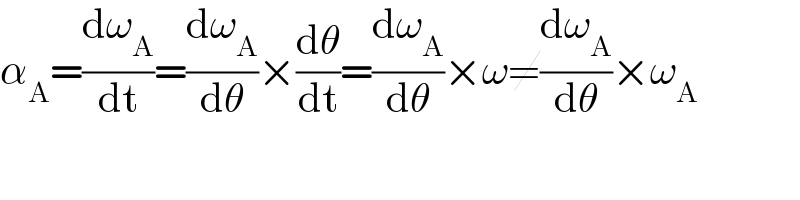
α_A =(dω_A /dt)=(dω_A /dθ)×(dθ/dt)=(dω_A /dθ)×ω≠(dω_A /dθ)×ω_A

$$\alpha_{\mathrm{A}} =\frac{\mathrm{d}\omega_{\mathrm{A}} }{\mathrm{dt}}=\frac{\mathrm{d}\omega_{\mathrm{A}} }{\mathrm{d}\theta}×\frac{\mathrm{d}\theta}{\mathrm{dt}}=\frac{\mathrm{d}\omega_{\mathrm{A}} }{\mathrm{d}\theta}×\omega\neq\frac{\mathrm{d}\omega_{\mathrm{A}} }{\mathrm{d}\theta}×\omega_{\mathrm{A}} \\ $$

Commented by ajfour last updated on 02/Nov/17

If initially θ=θ_0 (a little less than 90°, when system was released, find θ when disc A breaks contact with the wall. Friction is sufficient at wall and ground surface to permit pure rolling of the discs.

$${If}\:{initially}\:\theta=\theta_{\mathrm{0}} \:\left({a}\:{little}\:{less}\:\right. \\ $$$${than}\:\mathrm{90}°,\:{when}\:{system}\:{was}\:{released}, \\ $$$${find}\:\theta\:{when}\:{disc}\:{A}\:{breaks}\:{contact} \\ $$$${with}\:{the}\:{wall}.\:{Friction}\:{is}\:{sufficient} \\ $$$${at}\:{wall}\:{and}\:{ground}\:{surface}\:{to}\: \\ $$$${permit}\:{pure}\:{rolling}\:{of}\:{the}\:{discs}. \\ $$

Commented by mrW1 last updated on 03/Nov/17

(R+Lcos θ,R)=center of disc B (R,R+Lsin θ)=center of disc A (R+(L/2)cos θ,R+(L/2)sin θ)=center of rod C ω=(dθ/dt) (=ω_C ) v_A =(dy_A /dt)=Lcos θ ω u_B =(dx_B /dt)=−Lsin θ ω v_C =(L/2)cos θ ω u_C =−(L/2)sin θ ω ω_A =(v_A /R)=(L/R)cos θ ω ω_B =(u_B /R)=−(L/R)sin θ ω I_A =I_B =((MR^2 )/2) I_C =((mL^2 )/(12)) KE_A =(1/2)ML^2 cos^2 θ ω^2 +(1/2)×((MR^2 )/2)×(L^2 /R^2 )cos^2 θ ω^2 =((3ML^2 cos^2 θ)/4) ω^2 KE_B =(1/2)ML^2 sin^2 θ ω^2 +(1/2)×((MR^2 )/2)×(L^2 /R^2 )sin^2 θ ω^2 =((3ML^2 sin^2 θ)/4) ω^2 KE_C =(1/2)m(L^2 /4) ω^2 +(1/2)×((mL^2 )/(12)) ω^2 =((mL^2 )/6) ω^2 KE=(((3M)/4)+(m/6))L^2 ω^2 PE=−(M+(m/2))gL(sin θ_0 −sin θ) (((3M)/4)+(m/6))L^2 ω^2 =(M+(m/2))gL(sin θ_0 −sin θ) (9(M/m)+2)Lω^2 =(12(M/m)+6)g(sin θ_0 −sin θ) ω^2 =(g/L)×((12(M/m)+6)/(9(M/m)+2))×(sin θ_0 −sin θ) with a^2 =(g/L)×((12(M/m)+6)/(9(M/m)+2)), b=sin θ_0 ω^2 =a^2 (b−sin θ) ⇒ω=a(√(b−sin θ)) ω_A =(L/R)cos θ ω=((aL)/R)cos θ(√(b−sin θ)) α_A =ω(dω_A /dθ)=((a^2 L)/R)(√(b−sin θ))×[−sin θ(√(b−sin θ))−cos θ((cos θ)/(2(√(b−sin θ))))] α_A =((a^2 L)/(2R))×[3sin^2 θ−2bsin θ−1] when the contact with wall breaks, I_A α_A =0 ⇒3sin^2 θ−2bsin θ−1=0 ⇒sin θ=((b+(√(b^2 +3)))/3)=((sin θ_0 +(√(sin^2 θ_0 +3)))/3) ⇒θ=sin^(−1) [((sin θ_0 +(√(sin^2 θ_0 +3)))/3)]>θ_0 ...but θ should < θ_0 , so something is wrong .... ... or the contact will not break! ....

$$\left(\mathrm{R}+\mathrm{Lcos}\:\theta,\mathrm{R}\right)=\mathrm{center}\:\mathrm{of}\:\mathrm{disc}\:\mathrm{B} \\ $$$$\left(\mathrm{R},\mathrm{R}+\mathrm{Lsin}\:\theta\right)=\mathrm{center}\:\mathrm{of}\:\mathrm{disc}\:\mathrm{A} \\ $$$$\left(\mathrm{R}+\frac{\mathrm{L}}{\mathrm{2}}\mathrm{cos}\:\theta,\mathrm{R}+\frac{\mathrm{L}}{\mathrm{2}}\mathrm{sin}\:\theta\right)=\mathrm{center}\:\mathrm{of}\:\mathrm{rod}\:\mathrm{C} \\ $$$$\omega=\frac{\mathrm{d}\theta}{\mathrm{dt}}\:\left(=\omega_{\mathrm{C}} \right) \\ $$$$\mathrm{v}_{\mathrm{A}} =\frac{\mathrm{dy}_{\mathrm{A}} }{\mathrm{dt}}=\mathrm{Lcos}\:\theta\:\omega \\ $$$$\mathrm{u}_{\mathrm{B}} =\frac{\mathrm{dx}_{\mathrm{B}} }{\mathrm{dt}}=−\mathrm{Lsin}\:\theta\:\omega \\ $$$$\mathrm{v}_{\mathrm{C}} =\frac{\mathrm{L}}{\mathrm{2}}\mathrm{cos}\:\theta\:\omega \\ $$$$\mathrm{u}_{\mathrm{C}} =−\frac{\mathrm{L}}{\mathrm{2}}\mathrm{sin}\:\theta\:\omega \\ $$$$\omega_{\mathrm{A}} =\frac{\mathrm{v}_{\mathrm{A}} }{\mathrm{R}}=\frac{\mathrm{L}}{\mathrm{R}}\mathrm{cos}\:\theta\:\omega \\ $$$$\omega_{\mathrm{B}} =\frac{\mathrm{u}_{\mathrm{B}} }{\mathrm{R}}=−\frac{\mathrm{L}}{\mathrm{R}}\mathrm{sin}\:\theta\:\omega \\ $$$$\mathrm{I}_{\mathrm{A}} =\mathrm{I}_{\mathrm{B}} =\frac{\mathrm{MR}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{C}} =\frac{\mathrm{mL}^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\mathrm{KE}_{\mathrm{A}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ML}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\:\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{MR}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{L}^{\mathrm{2}} }{\mathrm{R}^{\mathrm{2}} }\mathrm{cos}^{\mathrm{2}} \:\theta\:\omega^{\mathrm{2}} =\frac{\mathrm{3ML}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{4}}\:\omega^{\mathrm{2}} \\ $$$$\mathrm{KE}_{\mathrm{B}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ML}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\:\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{MR}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{L}^{\mathrm{2}} }{\mathrm{R}^{\mathrm{2}} }\mathrm{sin}^{\mathrm{2}} \:\theta\:\omega^{\mathrm{2}} =\frac{\mathrm{3ML}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{4}}\:\omega^{\mathrm{2}} \\ $$$$\mathrm{KE}_{\mathrm{C}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}\frac{\mathrm{L}^{\mathrm{2}} }{\mathrm{4}}\:\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{mL}^{\mathrm{2}} }{\mathrm{12}}\:\omega^{\mathrm{2}} =\frac{\mathrm{mL}^{\mathrm{2}} }{\mathrm{6}}\:\omega^{\mathrm{2}} \\ $$$$\mathrm{KE}=\left(\frac{\mathrm{3M}}{\mathrm{4}}+\frac{\mathrm{m}}{\mathrm{6}}\right)\mathrm{L}^{\mathrm{2}} \omega^{\mathrm{2}} \\ $$$$\mathrm{PE}=−\left(\mathrm{M}+\frac{\mathrm{m}}{\mathrm{2}}\right)\mathrm{gL}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$\left(\frac{\mathrm{3M}}{\mathrm{4}}+\frac{\mathrm{m}}{\mathrm{6}}\right)\mathrm{L}^{\mathrm{2}} \omega^{\mathrm{2}} =\left(\mathrm{M}+\frac{\mathrm{m}}{\mathrm{2}}\right)\mathrm{gL}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$\left(\mathrm{9}\frac{\mathrm{M}}{\mathrm{m}}+\mathrm{2}\right)\mathrm{L}\omega^{\mathrm{2}} =\left(\mathrm{12}\frac{\mathrm{M}}{\mathrm{m}}+\mathrm{6}\right)\mathrm{g}\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$\omega^{\mathrm{2}} =\frac{\mathrm{g}}{\mathrm{L}}×\frac{\mathrm{12}\frac{\mathrm{M}}{\mathrm{m}}+\mathrm{6}}{\mathrm{9}\frac{\mathrm{M}}{\mathrm{m}}+\mathrm{2}}×\left(\mathrm{sin}\:\theta_{\mathrm{0}} −\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{with}\:\mathrm{a}^{\mathrm{2}} =\frac{\mathrm{g}}{\mathrm{L}}×\frac{\mathrm{12}\frac{\mathrm{M}}{\mathrm{m}}+\mathrm{6}}{\mathrm{9}\frac{\mathrm{M}}{\mathrm{m}}+\mathrm{2}},\:\mathrm{b}=\mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$$\omega^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow\omega=\mathrm{a}\sqrt{\mathrm{b}−\mathrm{sin}\:\theta} \\ $$$$\omega_{\mathrm{A}} =\frac{\mathrm{L}}{\mathrm{R}}\mathrm{cos}\:\theta\:\omega=\frac{\mathrm{aL}}{\mathrm{R}}\mathrm{cos}\:\theta\sqrt{\mathrm{b}−\mathrm{sin}\:\theta} \\ $$$$\alpha_{\mathrm{A}} =\omega\frac{\mathrm{d}\omega_{\mathrm{A}} }{\mathrm{d}\theta}=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{L}}{\mathrm{R}}\sqrt{\mathrm{b}−\mathrm{sin}\:\theta}×\left[−\mathrm{sin}\:\theta\sqrt{\mathrm{b}−\mathrm{sin}\:\theta}−\mathrm{cos}\:\theta\frac{\mathrm{cos}\:\theta}{\mathrm{2}\sqrt{\mathrm{b}−\mathrm{sin}\:\theta}}\right] \\ $$$$\alpha_{\mathrm{A}} =\frac{\mathrm{a}^{\mathrm{2}} \mathrm{L}}{\mathrm{2R}}×\left[\mathrm{3sin}^{\mathrm{2}} \:\theta−\mathrm{2bsin}\:\theta−\mathrm{1}\right] \\ $$$$\mathrm{when}\:\mathrm{the}\:\mathrm{contact}\:\mathrm{with}\:\mathrm{wall}\:\mathrm{breaks}, \\ $$$$\mathrm{I}_{\mathrm{A}} \alpha_{\mathrm{A}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{3sin}^{\mathrm{2}} \:\theta−\mathrm{2bsin}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{b}+\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{3}}=\frac{\mathrm{sin}\:\theta_{\mathrm{0}} +\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} +\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \left[\frac{\mathrm{sin}\:\theta_{\mathrm{0}} +\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} +\mathrm{3}}}{\mathrm{3}}\right]>\theta_{\mathrm{0}} \\ $$$$ \\ $$$$...\mathrm{but}\:\theta\:\mathrm{should}\:<\:\theta_{\mathrm{0}} ,\:\mathrm{so}\:\mathrm{something}\:\mathrm{is}\:\mathrm{wrong}\:.... \\ $$$$...\:\mathrm{or}\:\mathrm{the}\:\mathrm{contact}\:\mathrm{will}\:\mathrm{not}\:\mathrm{break}!\:.... \\ $$

Commented by ajfour last updated on 03/Nov/17

Thank you Sir, let me also attempt, after your guidelines. But how did you infer θ > θ_0 i dont think so, your answer seems correct and logical, just that α_A =0 doesnot necessarily imply that contact with wall breaks, a_A and hence friction at wall be zero for α_A to be zero.. contact might still persist. there is just a good chance its not certain.

$${Thank}\:{you}\:{Sir},\:{let}\:{me}\:{also} \\ $$$${attempt},\:{after}\:\:{your}\:{guidelines}. \\ $$$${But}\:{how}\:{did}\:{you}\:{infer}\:\theta\:>\:\theta_{\mathrm{0}} \\ $$$${i}\:{dont}\:{think}\:{so},\:{your}\:{answer} \\ $$$${seems}\:{correct}\:{and}\:{logical},\:{just} \\ $$$${that}\:\alpha_{{A}} =\mathrm{0}\:{doesnot}\:{necessarily} \\ $$$${imply}\:{that}\:{contact}\:{with}\:{wall} \\ $$$${breaks},\:{a}_{{A}} \:{and}\:{hence}\:{friction} \\ $$$${at}\:{wall}\:{be}\:{zero}\:{for}\:\alpha_{{A}} \:{to}\:{be}\:{zero}.. \\ $$$${contact}\:{might}\:{still}\:{persist}. \\ $$$${there}\:{is}\:{just}\:{a}\:{good}\:{chance}\:{its}\:{not} \\ $$$${certain}. \\ $$

Commented by ajfour last updated on 03/Nov/17

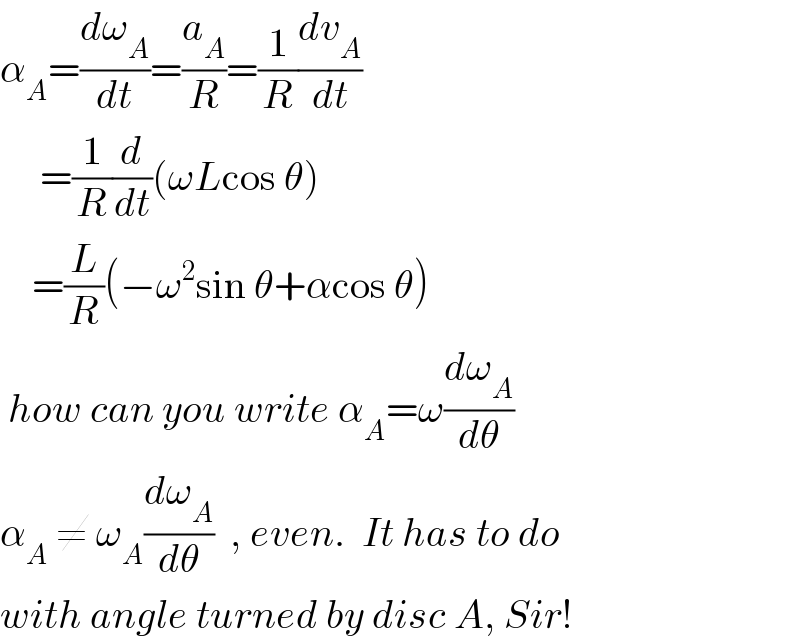
α_A =(dω_A /dt)=(a_A /R)=(1/R)(dv_A /dt) =(1/R)(d/dt)(ωLcos θ) =(L/R)(−ω^2 sin θ+αcos θ) how can you write α_A =ω(dω_A /dθ) α_A ≠ ω_A (dω_A /dθ) , even. It has to do with angle turned by disc A, Sir!

$$\alpha_{{A}} =\frac{{d}\omega_{{A}} }{{dt}}=\frac{{a}_{{A}} }{{R}}=\frac{\mathrm{1}}{{R}}\frac{{dv}_{{A}} }{{dt}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{{R}}\frac{{d}}{{dt}}\left(\omega{L}\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:=\frac{{L}}{{R}}\left(−\omega^{\mathrm{2}} \mathrm{sin}\:\theta+\alpha\mathrm{cos}\:\theta\right) \\ $$$$\:{how}\:{can}\:{you}\:{write}\:\alpha_{{A}} =\omega\frac{{d}\omega_{{A}} }{{d}\theta} \\ $$$$\alpha_{{A}} \:\neq\:\omega_{{A}} \frac{{d}\omega_{{A}} }{{d}\theta}\:\:,\:{even}.\:\:{It}\:{has}\:{to}\:{do} \\ $$$${with}\:{angle}\:{turned}\:{by}\:{disc}\:{A},\:{Sir}! \\ $$

Commented by mrW1 last updated on 03/Nov/17

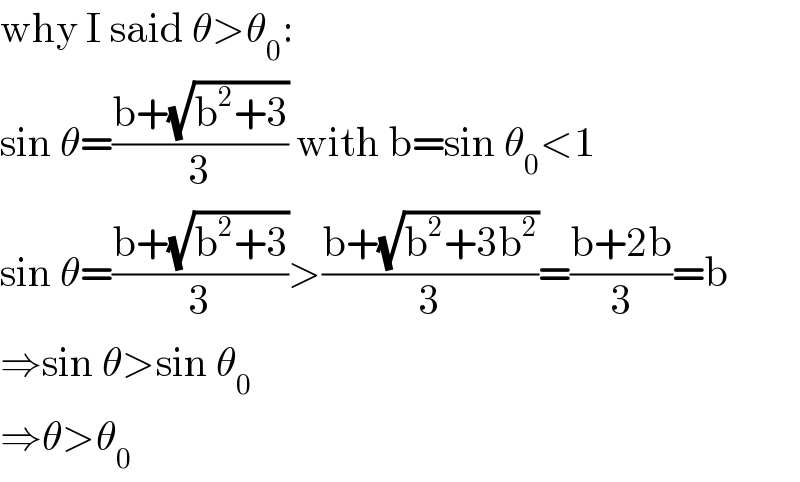
why I said θ>θ_0 : sin θ=((b+(√(b^2 +3)))/3) with b=sin θ_0 <1 sin θ=((b+(√(b^2 +3)))/3)>((b+(√(b^2 +3b^2 )))/3)=((b+2b)/3)=b ⇒sin θ>sin θ_0 ⇒θ>θ_0

$$\mathrm{why}\:\mathrm{I}\:\mathrm{said}\:\theta>\theta_{\mathrm{0}} : \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{b}+\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{3}}\:\mathrm{with}\:\mathrm{b}=\mathrm{sin}\:\theta_{\mathrm{0}} <\mathrm{1} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{b}+\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{3}}>\frac{\mathrm{b}+\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{3b}^{\mathrm{2}} }}{\mathrm{3}}=\frac{\mathrm{b}+\mathrm{2b}}{\mathrm{3}}=\mathrm{b} \\ $$$$\Rightarrow\mathrm{sin}\:\theta>\mathrm{sin}\:\theta_{\mathrm{0}} \\ $$$$\Rightarrow\theta>\theta_{\mathrm{0}} \\ $$

Commented by mrW1 last updated on 03/Nov/17

To ajfour sir: My consideration is: when the contact with the wall breaks, there is no normal force N and no friction force f between disc A and the wall. no friction force f means α_A =0. but α_A =0 doesn′t mean N=0, and if N≠0, it means there is a contact. but we can always say: if α_A ≠0, then f≠0, that means there is contact. according to my result, α_A ≠0 for 0<θ<θ_0 , that means there is always contact with the wall. I am really confused.

$$\mathrm{To}\:\mathrm{ajfour}\:\mathrm{sir}: \\ $$$$\mathrm{My}\:\mathrm{consideration}\:\mathrm{is}:\:\mathrm{when}\:\mathrm{the}\:\mathrm{contact} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{wall}\:\mathrm{breaks},\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\: \\ $$$$\mathrm{normal}\:\mathrm{force}\:\mathrm{N}\:\mathrm{and}\:\mathrm{no}\:\mathrm{friction}\:\mathrm{force}\:\mathrm{f} \\ $$$$\mathrm{between}\:\mathrm{disc}\:\mathrm{A}\:\mathrm{and}\:\mathrm{the}\:\mathrm{wall}.\:\mathrm{no} \\ $$$$\mathrm{friction}\:\mathrm{force}\:\mathrm{f}\:\mathrm{means}\:\alpha_{\mathrm{A}} =\mathrm{0}.\:\mathrm{but} \\ $$$$\alpha_{\mathrm{A}} =\mathrm{0}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{mean}\:\mathrm{N}=\mathrm{0},\:\mathrm{and}\:\mathrm{if}\:\mathrm{N}\neq\mathrm{0},\:\mathrm{it} \\ $$$$\mathrm{means}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{contact}. \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{can}\:\mathrm{always}\:\mathrm{say}:\:\mathrm{if}\:\alpha_{\mathrm{A}} \neq\mathrm{0},\:\mathrm{then} \\ $$$$\mathrm{f}\neq\mathrm{0},\:\mathrm{that}\:\mathrm{means}\:\mathrm{there}\:\mathrm{is}\:\mathrm{contact}. \\ $$$$\mathrm{according}\:\mathrm{to}\:\mathrm{my}\:\mathrm{result},\:\alpha_{\mathrm{A}} \:\neq\mathrm{0}\:\mathrm{for} \\ $$$$\mathrm{0}<\theta<\theta_{\mathrm{0}} ,\:\mathrm{that}\:\mathrm{means}\:\mathrm{there}\:\mathrm{is}\:\mathrm{always} \\ $$$$\mathrm{contact}\:\mathrm{with}\:\mathrm{the}\:\mathrm{wall}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{really}\:\mathrm{confused}. \\ $$

Commented by mrW1 last updated on 03/Nov/17

ω=a(√(b−sin θ)) α=(dω/dt)=ω(dω/dθ)=a^2 (√(b−sin θ))×((−cos θ)/(2(√(b−sin θ))))=−((a^2 cos θ)/2) α_A =....=(dω_A /dt)=(L/R)(−ω^2 sin θ+αcos θ) =(L/R)[−a^2 (b−sin θ)sin θ−((a^2 cos^2 θ)/2)] =((a^2 L)/(2R))[3sin^2 θ−2bsin θ−1] this is the same as I got.

$$\omega=\mathrm{a}\sqrt{\mathrm{b}−\mathrm{sin}\:\theta} \\ $$$$\alpha=\frac{\mathrm{d}\omega}{\mathrm{dt}}=\omega\frac{\mathrm{d}\omega}{\mathrm{d}\theta}=\mathrm{a}^{\mathrm{2}} \sqrt{\mathrm{b}−\mathrm{sin}\:\theta}×\frac{−\mathrm{cos}\:\theta}{\mathrm{2}\sqrt{\mathrm{b}−\mathrm{sin}\:\theta}}=−\frac{\mathrm{a}^{\mathrm{2}} \mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\alpha_{\mathrm{A}} =....=\frac{\mathrm{d}\omega_{\mathrm{A}} }{\mathrm{dt}}=\frac{{L}}{{R}}\left(−\omega^{\mathrm{2}} \mathrm{sin}\:\theta+\alpha\mathrm{cos}\:\theta\right) \\ $$$$=\frac{\mathrm{L}}{\mathrm{R}}\left[−\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}−\mathrm{sin}\:\theta\right)\mathrm{sin}\:\theta−\frac{\mathrm{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{a}^{\mathrm{2}} \mathrm{L}}{\mathrm{2R}}\left[\mathrm{3sin}^{\mathrm{2}} \:\theta−\mathrm{2bsin}\:\theta−\mathrm{1}\right] \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{I}\:\mathrm{got}. \\ $$

Commented by ajfour last updated on 03/Nov/17

I disagree, contact breaks as soon as disc A develops acceleration towards right, this takes place because (a_B +𝛚^2 lcos 𝛉) becomes > 𝛂lsin 𝛉 as soon as this happens contact breaks and disc A is no more rolling so 𝛚_A = (v_A /R) is no more in applicable. I shall need some time to post my analysis but presently i shall say that wben contact breaks sin 𝛉=(4/7)((((M/m)+(1/3))/((M/m)+(2/7))))sin θ_0 .

$${I}\:{disagree},\:{contact}\:{breaks}\:{as}\:{soon} \\ $$$${as}\:{disc}\:{A}\:{develops}\:{acceleration} \\ $$$${towards}\:{right},\:{this}\:{takes}\:{place} \\ $$$${because}\: \\ $$$$\left(\boldsymbol{{a}}_{\boldsymbol{{B}}} +\boldsymbol{\omega}^{\mathrm{2}} \boldsymbol{{l}}\mathrm{cos}\:\boldsymbol{\theta}\right)\:{becomes}\:>\:\boldsymbol{\alpha{l}}\mathrm{sin}\:\boldsymbol{\theta} \\ $$$${as}\:{soon}\:{as}\:{this}\:{happens}\:{contact} \\ $$$${breaks}\:{and}\:{disc}\:{A}\:{is}\:{no}\:{more} \\ $$$${rolling}\:{so}\:\boldsymbol{\omega}_{\boldsymbol{{A}}} =\:\frac{\boldsymbol{{v}}_{\boldsymbol{{A}}} }{{R}}\:\:\:{is}\:{no}\:{more} \\ $$$${in}\:{applicable}. \\ $$$${I}\:{shall}\:{need}\:{some}\:{time}\:{to}\:{post} \\ $$$${my}\:{analysis}\:{but}\:{presently}\:{i}\:{shall} \\ $$$${say}\:{that}\:{wben}\:{contact}\:{breaks} \\ $$$$\:\:\:\:\mathrm{sin}\:\boldsymbol{\theta}=\frac{\mathrm{4}}{\mathrm{7}}\left(\frac{\frac{{M}}{{m}}+\frac{\mathrm{1}}{\mathrm{3}}}{\frac{{M}}{{m}}+\frac{\mathrm{2}}{\mathrm{7}}}\right)\mathrm{sin}\:\theta_{\mathrm{0}} \:. \\ $$$$\:\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com