
Question Number 23796 by tapan das last updated on 06/Nov/17
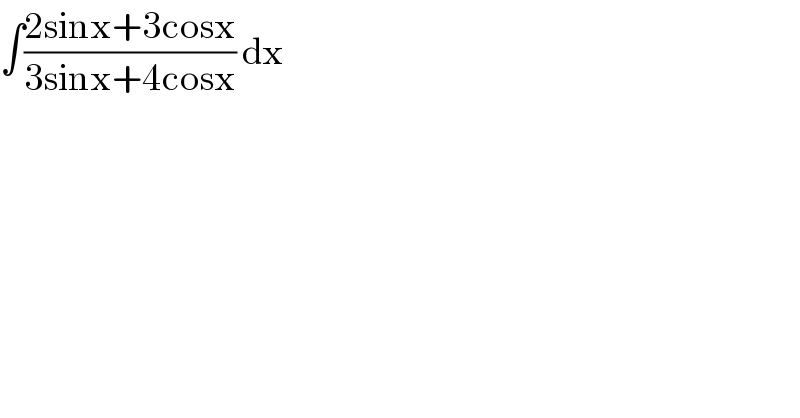
$$\int\frac{\mathrm{2sinx}+\mathrm{3cosx}}{\mathrm{3sinx}+\mathrm{4cosx}}\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 06/Nov/17

$$\mathrm{2sin}\:{x}+\mathrm{3cos}\:{x}={A}\left(\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{B}\left(\mathrm{3cos}\:{x}−\mathrm{4sin}\:{x}\right) \\ $$$$\Rightarrow\:\mathrm{3}{A}−\mathrm{4}{B}=\mathrm{2}\:\:{and} \\ $$$$\:\:\:\:\:\:\mathrm{4}{A}+\mathrm{3}{B}=\mathrm{3} \\ $$$$\Rightarrow\:\:{A}=\frac{\mathrm{18}}{\mathrm{25}}\:\:,\:{B}=\frac{\mathrm{1}}{\mathrm{25}}\:\:;\:{So} \\ $$$$\int\frac{\mathrm{2sin}\:{x}+\mathrm{3cos}\:{x}}{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}}{dx}\:=\frac{\mathrm{18}}{\mathrm{25}}\int{dx}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{25}}\int\frac{\mathrm{3cos}\:{x}−\mathrm{4sin}\:{x}}{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{18}{x}}{\mathrm{25}}+\frac{\mathrm{1}}{\mathrm{25}}\mathrm{ln}\:\mid\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}\mid+{C}\:. \\ $$
