Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 2393 by 123456 last updated on 19/Nov/15

f:[0,1]→R x=a_0 ,a_1 a_2 a_3 ... f(x)=Σ_(i=0) ^(+∞) a_i is f(x) continuous in all x∈[0,1] f(0,9999...)=?? f(1)=1

$${f}:\left[\mathrm{0},\mathrm{1}\right]\rightarrow\mathbb{R} \\ $$$${x}={a}_{\mathrm{0}} ,{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} ... \\ $$$${f}\left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{+\infty} {\sum}}{a}_{{i}} \\ $$$$\mathrm{is}\:{f}\left({x}\right)\:\mathrm{continuous}\:\mathrm{in}\:\mathrm{all}\:{x}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$${f}\left(\mathrm{0},\mathrm{9999}...\right)=?? \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$

Commented by prakash jain last updated on 19/Nov/15

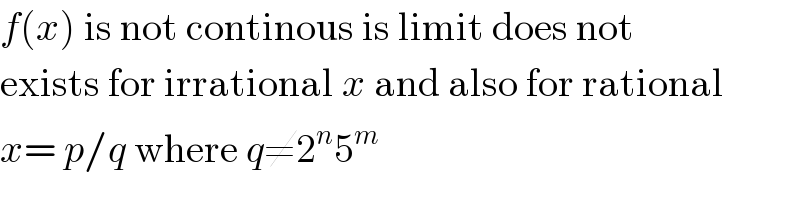
f(x) is not continous is limit does not exists for irrational x and also for rational x= p/q where q≠2^n 5^m

$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{continous}\:\mathrm{is}\:\mathrm{limit}\:\mathrm{does}\:\mathrm{not} \\ $$$$\mathrm{exists}\:\mathrm{for}\:\mathrm{irrational}\:{x}\:\mathrm{and}\:\mathrm{also}\:\mathrm{for}\:\mathrm{rational} \\ $$$${x}=\:{p}/{q}\:\mathrm{where}\:{q}\neq\mathrm{2}^{{n}} \mathrm{5}^{{m}} \\ $$

Commented by prakash jain last updated on 19/Nov/15

I don′t think there is any real number like 0.99999.... (infinite times). It is same as 1.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{there}\:\mathrm{is}\:\mathrm{any}\:\mathrm{real}\:\mathrm{number}\:\mathrm{like} \\ $$$$\mathrm{0}.\mathrm{99999}....\:\left(\mathrm{infinite}\:\mathrm{times}\right).\:\mathrm{It}\:\mathrm{is}\:\:\mathrm{same}\:\mathrm{as}\:\mathrm{1}. \\ $$

Commented by prakash jain last updated on 19/Nov/15

What i mean is 0.999.. is a recurring decimal and hence rational. The rational number representing this number is 1. This is different from other rationals like 1/3. which can be represented both in recurring decimal and fraction notation. So for example 0.49999999999...(infinite times)=1/2

$$\mathrm{What}\:\mathrm{i}\:\mathrm{mean}\:\mathrm{is}\:\mathrm{0}.\mathrm{999}..\:\mathrm{is}\:\mathrm{a}\:\mathrm{recurring}\:\mathrm{decimal} \\ $$$$\mathrm{and}\:\mathrm{hence}\:\mathrm{rational}.\:\mathrm{The}\:\mathrm{rational}\:\mathrm{number} \\ $$$$\mathrm{representing}\:\mathrm{this}\:\mathrm{number}\:\mathrm{is}\:\mathrm{1}.\: \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{different}\:\mathrm{from}\:\mathrm{other}\:\mathrm{rationals} \\ $$$$\mathrm{like}\:\mathrm{1}/\mathrm{3}.\:\mathrm{which}\:\mathrm{can}\:\mathrm{be}\:\mathrm{represented}\:\mathrm{both} \\ $$$$\mathrm{in}\:\mathrm{recurring}\:\mathrm{decimal}\:\mathrm{and}\:\mathrm{fraction}\:\mathrm{notation}. \\ $$$$\mathrm{So}\:\mathrm{for}\:\mathrm{example} \\ $$$$\mathrm{0}.\mathrm{49999999999}...\left(\mathrm{infinite}\:\mathrm{times}\right)=\mathrm{1}/\mathrm{2} \\ $$

Answered by Filup last updated on 19/Nov/15

0.9^− is exactly equal to 1. Because of the infinite number of 9′s being appended, this makes it entirely equal. Think about it like this: If 1≠0.9^− , then: 0.9^− =0.999...9990000^− ... which is contradictory against the definition of recurring decimals. ALL recurring decimals are rational, thus: f(0.9^− )=f(1) iff 0.9^− is appended infinitly!

$$\mathrm{0}.\overset{−} {\mathrm{9}}\:\mathrm{is}\:\boldsymbol{{exactly}}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1}. \\ $$$$\mathrm{Because}\:\mathrm{of}\:\mathrm{the}\:\mathrm{infinite}\:\mathrm{number}\:\mathrm{of}\:\mathrm{9}'\mathrm{s} \\ $$$$\mathrm{being}\:\mathrm{appended},\:\mathrm{this}\:\mathrm{makes}\:\mathrm{it}\:\mathrm{entirely} \\ $$$$\mathrm{equal}. \\ $$$$ \\ $$$$\mathrm{Think}\:\mathrm{about}\:\mathrm{it}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\mathrm{If}\:\mathrm{1}\neq\mathrm{0}.\overset{−} {\mathrm{9}},\:{then}: \\ $$$$\mathrm{0}.\overset{−} {\mathrm{9}}=\mathrm{0}.\mathrm{999}...\mathrm{999000}\overset{−} {\mathrm{0}}...\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{contradictory}\:\mathrm{against}\:\mathrm{the}\:\mathrm{definition} \\ $$$$\mathrm{of}\:\mathrm{recurring}\:\mathrm{decimals}.\:\boldsymbol{{ALL}}\:\mathrm{recurring} \\ $$$$\mathrm{decimals}\:\mathrm{are}\:\mathrm{rational},\:{thus}: \\ $$$${f}\left(\mathrm{0}.\overset{−} {\mathrm{9}}\right)={f}\left(\mathrm{1}\right)\:\:\:{iff}\:\:\:\mathrm{0}.\overset{−} {\mathrm{9}}\:\mathrm{is}\:\mathrm{appended}\:\mathrm{infinitly}! \\ $$

Commented by prakash jain last updated on 19/Nov/15

Correct. 0.49^− =1/2 0.9^− =1. 1/2 =.5

$$\mathrm{Correct}. \\ $$$$\mathrm{0}.\mathrm{4}\overset{−} {\mathrm{9}}=\mathrm{1}/\mathrm{2} \\ $$$$\mathrm{0}.\overset{−} {\mathrm{9}}=\mathrm{1}. \\ $$$$\mathrm{1}/\mathrm{2}\:\:=.\mathrm{5} \\ $$

Commented by 123456 last updated on 19/Nov/15

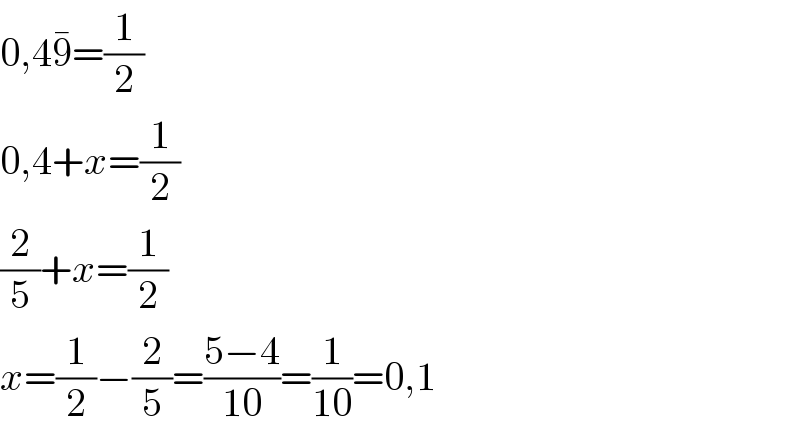
0,49^� =(1/2) 0,4+x=(1/2) (2/5)+x=(1/2) x=(1/2)−(2/5)=((5−4)/(10))=(1/(10))=0,1

$$\mathrm{0},\mathrm{4}\bar {\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{0},\mathrm{4}+{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{2}}{\mathrm{5}}+{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{5}−\mathrm{4}}{\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{10}}=\mathrm{0},\mathrm{1} \\ $$

Commented by prakash jain last updated on 20/Nov/15

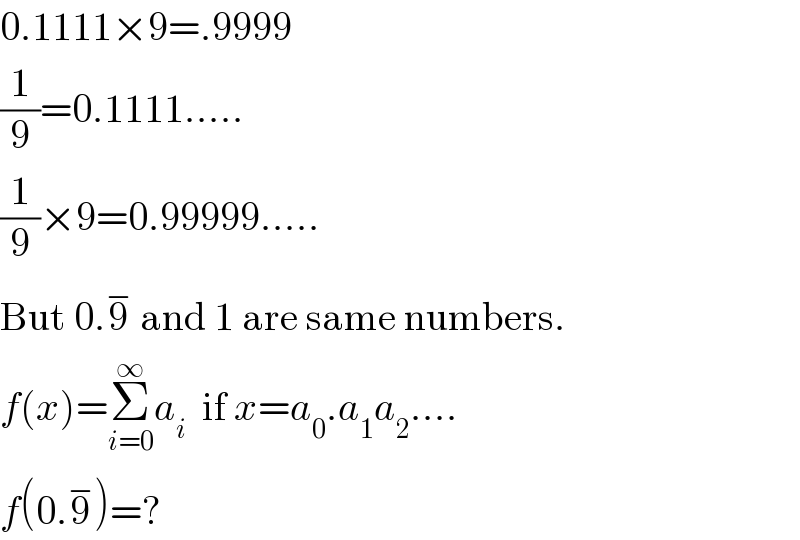
0.1111×9=.9999 (1/9)=0.1111..... (1/9)×9=0.99999..... But 0.9^− and 1 are same numbers. f(x)=Σ_(i=0) ^∞ a_i if x=a_0 .a_1 a_2 .... f(0.9^− )=?

$$\mathrm{0}.\mathrm{1111}×\mathrm{9}=.\mathrm{9999} \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}=\mathrm{0}.\mathrm{1111}..... \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}×\mathrm{9}=\mathrm{0}.\mathrm{99999}..... \\ $$$$\mathrm{But}\:\mathrm{0}.\overset{−} {\mathrm{9}}\:\mathrm{and}\:\mathrm{1}\:\mathrm{are}\:\mathrm{same}\:\mathrm{numbers}. \\ $$$${f}\left({x}\right)=\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{{i}} \:\:\mathrm{if}\:{x}={a}_{\mathrm{0}} .{a}_{\mathrm{1}} {a}_{\mathrm{2}} .... \\ $$$${f}\left(\mathrm{0}.\overset{−} {\mathrm{9}}\right)=? \\ $$

Commented by RasheedAhmad last updated on 19/Nov/15

One difference between 0.9_(−) ^(−) and 0.3_(−) ^(−) 0.3^(−) can be achieved by actual division process. 1÷3=0.3^(−) But 0.9^(−) cannot be achieved by actual process of division of any two integers. 0.9^(−) =1=(1/1) 1÷1 doesn′t yield 0.9999... it is simply 1 0.49^(−) is also like 0.9^(−) It cannot be achieved by actual process of division of any two integers. 1÷2 doesn′t yield 0.49999... it is simply 0.5

$$\underset{−} {\mathcal{O}{ne}\:{difference}\:{between}\:\mathrm{0}.\mathrm{9}} \\ $$$$\underset{−} {{and}\:\mathrm{0}.\mathrm{3}} \\ $$$$\mathrm{0}.\overline {\mathrm{3}}\:{can}\:{be}\:{achieved}\:{by}\:{actual} \\ $$$${division}\:{process}. \\ $$$$\mathrm{1}\boldsymbol{\div}\mathrm{3}=\mathrm{0}.\overline {\mathrm{3}} \\ $$$${But}\:\mathrm{0}.\overline {\mathrm{9}}\:{cannot}\:{be}\:{achieved}\:{by} \\ $$$${actual}\:{process}\:{of}\:{division} \\ $$$${of}\:{any}\:{two}\:{integers}. \\ $$$$\mathrm{0}.\overline {\mathrm{9}}=\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$\mathrm{1}\boldsymbol{\div}\mathrm{1}\:{doesn}'{t}\:{yield}\:\mathrm{0}.\mathrm{9999}... \\ $$$${it}\:{is}\:{simply}\:\mathrm{1} \\ $$$$\mathrm{0}.\mathrm{4}\overline {\mathrm{9}}\:{is}\:{also}\:{like}\:\mathrm{0}.\overline {\mathrm{9}} \\ $$$${It}\:{cannot}\:{be}\:{achieved}\:{by}\:{actual} \\ $$$${process}\:{of}\:{division}\:{of}\:{any}\:{two} \\ $$$${integers}. \\ $$$$\mathrm{1}\boldsymbol{\div}\mathrm{2}\:{doesn}'{t}\:{yield}\:\mathrm{0}.\mathrm{49999}... \\ $$$${it}\:{is}\:{simply}\:\mathrm{0}.\mathrm{5} \\ $$

Commented by 123456 last updated on 19/Nov/15

(a/9)=0,a^� a∈{0,1,2,3,4,5,6,7,8,9?} (9/9)=0,9999... 9∣9 0 1 9∣9 90⌊0,99... 81 90 81 ⋮ 4∣4 40 ⌊0,9... 36 40 ⋮

$$\frac{{a}}{\mathrm{9}}=\mathrm{0},\bar {{a}}\:\:\:{a}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9}?\right\} \\ $$$$\frac{\mathrm{9}}{\mathrm{9}}=\mathrm{0},\mathrm{9999}... \\ $$$$\mathrm{9}\mid\mathrm{9} \\ $$$$\mathrm{0}\:\:\mathrm{1} \\ $$$$\mathrm{9}\mid\mathrm{9} \\ $$$$\mathrm{90}\lfloor\mathrm{0},\mathrm{99}... \\ $$$$\mathrm{81} \\ $$$$\:\:\mathrm{90} \\ $$$$\:\:\mathrm{81} \\ $$$$\:\:\:\:\vdots \\ $$$$\mathrm{4}\mid\mathrm{4} \\ $$$$\mathrm{40}\:\lfloor\mathrm{0},\mathrm{9}... \\ $$$$\mathrm{36} \\ $$$$\:\:\:\mathrm{40} \\ $$$$\:\:\:\:\vdots \\ $$

Commented by Rasheed Soomro last updated on 20/Nov/15

′V Nice!′ for your deep approach! You have successfully showed/proved in various ways that 0.9^(−) =1 Actually I don′t deny the above. I only pointed out the difference between 0.3^(−) and 0.9^(−) 0.3^(−) is the result of ordinary division of two integers 1÷3=0.3333... whereas 0.9^(−) is not. You have also tried to show that 0.9^(−) can be achieved by ordinary division (9÷9) but in this connection you haven′t followed some rules of ordinary division. So I think 0.9^(−) ,0.49^(−) etc aren′t achievable by ordinary_(−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−) division of two integers._(−−−−−−−−−−−−−−−−−−−)

$$'{V}\:{Nice}!'\:\:{for}\:{your}\:{deep}\:{approach}! \\ $$$${You}\:{have}\:{successfully}\:{showed}/{proved}\:{in}\:{various}\:{ways}\:\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{0}.\overline {\mathrm{9}}=\mathrm{1} \\ $$$${Actually}\:{I}\:{don}'{t}\:{deny}\:{the}\:{above}.\:{I}\:{only}\:{pointed}\:{out} \\ $$$${the}\:{difference}\:{between}\:\mathrm{0}.\overline {\mathrm{3}}\:\:{and}\:\:\mathrm{0}.\overline {\mathrm{9}} \\ $$$$\mathrm{0}.\overline {\mathrm{3}}\:{is}\:{the}\:{result}\:{of}\:{ordinary}\:\:{division}\:{of}\:{two}\:{integers} \\ $$$$\mathrm{1}\boldsymbol{\div}\mathrm{3}=\mathrm{0}.\mathrm{3333}...\:\:{whereas}\:\:\mathrm{0}.\overline {\mathrm{9}}\:\:{is}\:{not}. \\ $$$${You}\:{have}\:{also}\:{tried}\:{to}\:{show}\:{that}\:\mathrm{0}.\overline {\mathrm{9}}\:{can}\:{be}\:{achieved} \\ $$$${by}\:{ordinary}\:\:{division}\:\left(\mathrm{9}\boldsymbol{\div}\mathrm{9}\right)\:{but}\:{in}\:{this}\:{connection}\:{you} \\ $$$${haven}'{t}\:{followed}\:{some}\:{rules}\:{of}\:{ordinary}\:{division}. \\ $$$$\underset{−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−} {{So}\:{I}\:{think}\:\mathrm{0}.\mathrm{9},\mathrm{0}.\mathrm{49}\:\:{etc}\:{aren}'{t}\:{achievable}\:{by}\:{ordinary}} \\ $$$$\underset{−−−−−−−−−−−−−−−−−−−} {{division}\:{of}\:{two}\:{integers}.} \\ $$$$ \\ $$

Commented by 123456 last updated on 19/Nov/15

0,9999... =9/10+9/10^2 +... =((9/10)/(1−1/10))=((9/10)/(9/10))=1 (infinite pg) or s=0,999.... 10s=9,999.... 9s=9 s=1 ps: 1=0,11111111...._2 since Σ_(i=1) ^(+∞) (1/2^i )=((1/2)/(1−1/2))=1 if f doenst is continuous them (dont sure) lim_(n→+∞) f(x_n )≠f(lim_(n→+∞) x_n ) in general them this have something about f(0,99...) and f(1) or ⌊0,999...⌋ and ⌊1⌋ or i think it have :v

$$\mathrm{0},\mathrm{9999}... \\ $$$$=\mathrm{9}/\mathrm{10}+\mathrm{9}/\mathrm{10}^{\mathrm{2}} +... \\ $$$$=\frac{\mathrm{9}/\mathrm{10}}{\mathrm{1}−\mathrm{1}/\mathrm{10}}=\frac{\mathrm{9}/\mathrm{10}}{\mathrm{9}/\mathrm{10}}=\mathrm{1}\:\left(\mathrm{infinite}\:\mathrm{pg}\right) \\ $$$$\mathrm{or} \\ $$$$\mathrm{s}=\mathrm{0},\mathrm{999}.... \\ $$$$\mathrm{10s}=\mathrm{9},\mathrm{999}.... \\ $$$$\mathrm{9s}=\mathrm{9} \\ $$$$\mathrm{s}=\mathrm{1} \\ $$$$\mathrm{ps}: \\ $$$$\mathrm{1}=\mathrm{0},\mathrm{11111111}...._{\mathrm{2}} \\ $$$$\mathrm{since} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{i}} }=\frac{\mathrm{1}/\mathrm{2}}{\mathrm{1}−\mathrm{1}/\mathrm{2}}=\mathrm{1} \\ $$$$\mathrm{if}\:{f}\:\mathrm{doenst}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{them}\:\left(\mathrm{dont}\:\mathrm{sure}\right) \\ $$$$\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}}\:{f}\left({x}_{{n}} \right)\neq{f}\left(\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:{x}_{{n}} \right)\:\mathrm{in}\:\mathrm{general} \\ $$$$\mathrm{them}\:\mathrm{this}\:\mathrm{have}\:\mathrm{something}\:\mathrm{about} \\ $$$${f}\left(\mathrm{0},\mathrm{99}...\right)\:\mathrm{and}\:{f}\left(\mathrm{1}\right)\:{or} \\ $$$$\lfloor\mathrm{0},\mathrm{999}...\rfloor\:\mathrm{and}\:\lfloor\mathrm{1}\rfloor \\ $$$$\mathrm{or}\:\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{have}\::\mathrm{v} \\ $$

Commented by Rasheed Soomro last updated on 20/Nov/15

0.9^(−) =1⇒f(0.9^(−) )=f(1)=1 On the other hand f(0.9^(−) )=9.∞=∞ That means to avoid contadiction we should deny the separte existence of 0.9^(−) and think ′ it is nothing but 1′ ? Similarly f(0.49^(−) )=f(0.5)=5?

$$\mathrm{0}.\overline {\mathrm{9}}=\mathrm{1}\Rightarrow{f}\left(\mathrm{0}.\overline {\mathrm{9}}\right)={f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${On}\:{the}\:{other}\:{hand}\:{f}\left(\mathrm{0}.\overline {\mathrm{9}}\right)=\mathrm{9}.\infty=\infty \\ $$$${That}\:{means}\:{to}\:{avoid}\:{contadiction}\:{we}\:{should} \\ $$$${deny}\:{the}\:{separte}\:{existence}\:{of}\:\mathrm{0}.\overline {\mathrm{9}}\:{and}\:{think}\:'\:{it}\:{is} \\ $$$${nothing}\:{but}\:\mathrm{1}'\:? \\ $$$${Similarly}\:{f}\left(\mathrm{0}.\mathrm{4}\overline {\mathrm{9}}\right)={f}\left(\mathrm{0}.\mathrm{5}\right)=\mathrm{5}? \\ $$

Commented by 123456 last updated on 20/Nov/15

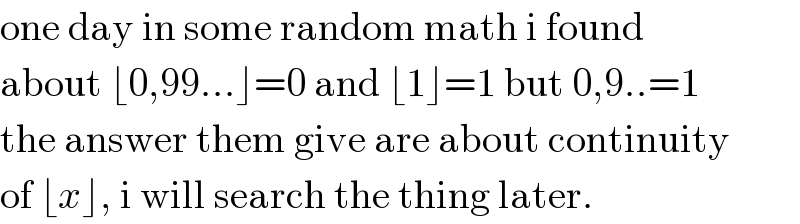
one day in some random math i found about ⌊0,99...⌋=0 and ⌊1⌋=1 but 0,9..=1 the answer them give are about continuity of ⌊x⌋, i will search the thing later.

$$\mathrm{one}\:\mathrm{day}\:\mathrm{in}\:\mathrm{some}\:\mathrm{random}\:\mathrm{math}\:\mathrm{i}\:\mathrm{found} \\ $$$$\mathrm{about}\:\lfloor\mathrm{0},\mathrm{99}...\rfloor=\mathrm{0}\:\mathrm{and}\:\lfloor\mathrm{1}\rfloor=\mathrm{1}\:\mathrm{but}\:\mathrm{0},\mathrm{9}..=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{them}\:\mathrm{give}\:\mathrm{are}\:\mathrm{about}\:\mathrm{continuity} \\ $$$$\mathrm{of}\:\lfloor{x}\rfloor,\:\mathrm{i}\:\mathrm{will}\:\mathrm{search}\:\mathrm{the}\:\mathrm{thing}\:\mathrm{later}. \\ $$

Commented by Rasheed Soomro last updated on 21/Nov/15

I ′ll wait for update!

$$\mathcal{I}\:'{ll}\:{wait}\:{for}\:{update}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com