Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 2400 by Filup last updated on 19/Nov/15

According to Wikipedia and WolframAlpha, the sign function, sgn(x), is defined as: sgn(x)≡(x/(∣x∣))=((∣x∣)/x) for x≠0 and satisfies: sgn(x)=(√x)(√(1/x)) but sgn(0)=0 In short: sgn(x)= { ((1 for x>0)),((0 for x=0)),((−1 for x<0)) :} Why does sgn(0)=0?

$$\mathrm{According}\:\mathrm{to}\:\mathrm{Wikipedia}\:\mathrm{and}\:\mathrm{WolframAlpha}, \\ $$$$\mathrm{the}\:\mathrm{sign}\:\mathrm{function},\:\mathrm{sgn}\left({x}\right),\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as}: \\ $$$$ \\ $$$$\mathrm{sgn}\left({x}\right)\equiv\frac{{x}}{\mid{x}\mid}=\frac{\mid{x}\mid}{{x}}\:\:\:\mathrm{for}\:{x}\neq\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{satisfies}: \\ $$$$\mathrm{sgn}\left({x}\right)=\sqrt{{x}}\sqrt{\frac{\mathrm{1}}{{x}}} \\ $$$$\boldsymbol{{but}} \\ $$$$\mathrm{sgn}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{In}\:\mathrm{short}: \\ $$$$ \\ $$$$\mathrm{sgn}\left({x}\right)=\begin{cases}{\mathrm{1}\:\:\:\:\:\mathrm{for}\:{x}>\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\mathrm{for}\:{x}=\mathrm{0}}\\{−\mathrm{1}\:\mathrm{for}\:{x}<\mathrm{0}}\end{cases} \\ $$$$ \\ $$$$\mathrm{Why}\:\mathrm{does}\:\mathrm{sgn}\left(\mathrm{0}\right)=\mathrm{0}? \\ $$

Commented by Rasheed Soomro last updated on 19/Nov/15

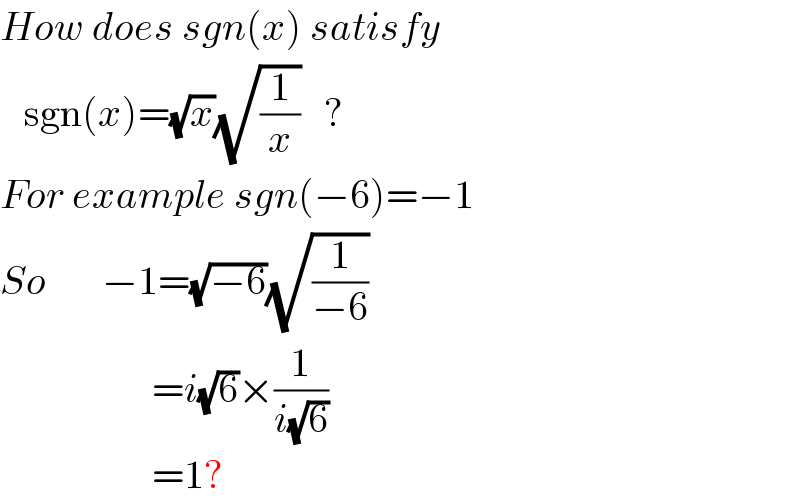
How does sgn(x) satisfy sgn(x)=(√x)(√(1/x)) ? For example sgn(−6)=−1 So −1=(√(−6))(√(1/(−6))) =i(√6)×(1/(i(√6))) =1?

$${How}\:{does}\:{sgn}\left({x}\right)\:{satisfy} \\ $$$$\:\:\:\mathrm{sgn}\left({x}\right)=\sqrt{{x}}\sqrt{\frac{\mathrm{1}}{{x}}}\:\:\:? \\ $$$${For}\:{example}\:{sgn}\left(−\mathrm{6}\right)=−\mathrm{1} \\ $$$${So}\:\:\:\:\:\:\:−\mathrm{1}=\sqrt{−\mathrm{6}}\sqrt{\frac{\mathrm{1}}{−\mathrm{6}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={i}\sqrt{\mathrm{6}}×\frac{\mathrm{1}}{{i}\sqrt{\mathrm{6}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}? \\ $$

Commented by Filup last updated on 20/Nov/15

I′m not sure how it satisfies. That was Just what I found online

$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{how}\:\mathrm{it}\:\mathrm{satisfies}.\:\mathrm{That}\:\mathrm{was} \\ $$$$\mathrm{Just}\:\mathrm{what}\:\mathrm{I}\:\mathrm{found}\:\mathrm{online} \\ $$

Commented by Rasheed Soomro last updated on 20/Nov/15

Why does sgn(0)=0? An Interpretation for sgn(0)=0 Here 1,0,−1 are representative_(−) elements only. • ′1′ represents the situation x>0 •Opposite situation x<0 is represented by ′ −1 ′ (which is opposite of ′ 1 ′ ) • x=0 is neutral situation which should be represented by neutral element that is ′ 0 ′

$$\mathrm{Why}\:\mathrm{does}\:\mathrm{sgn}\left(\mathrm{0}\right)=\mathrm{0}? \\ $$$$\mathcal{A}{n}\:\mathcal{I}{nterpretation}\:{for}\:\:{sgn}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${Here}\:\mathrm{1},\mathrm{0},−\mathrm{1}\:{are}\:\:\underset{−} {{representative}}\:\:{elements}\:{only}. \\ $$$$\:\bullet\:'\mathrm{1}'\:\:{represents}\:{the}\:{situation}\:{x}>\mathrm{0}\: \\ $$$$\bullet{Opposite}\:{situation}\:{x}<\mathrm{0}\:{is}\:{represented}\:{by}\:'\:−\mathrm{1}\:'\:\left({which}\:{is}\right. \\ $$$$\left.\:\:\:{opposite}\:{of}\:'\:\mathrm{1}\:'\:\right) \\ $$$$\bullet\:{x}=\mathrm{0}\:{is}\:{neutral}\:{situation}\:{which}\:{should}\:{be}\:{represented} \\ $$$$\:\:\:\:{by}\:{neutral}\:{element}\:{that}\:{is}\:'\:\mathrm{0}\:' \\ $$

Commented by prakash jain last updated on 20/Nov/15

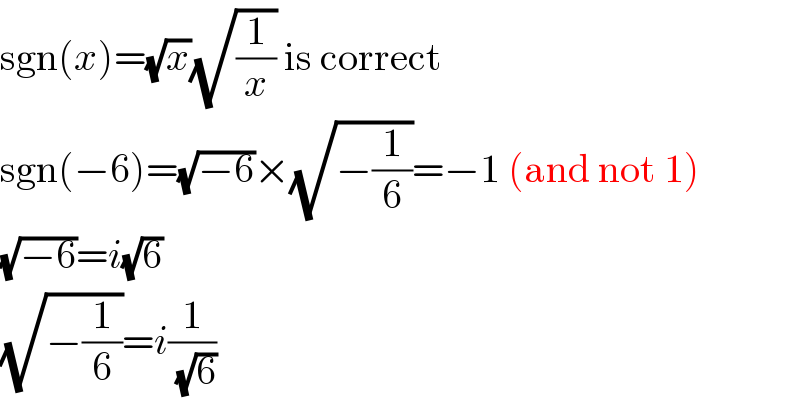
sgn(x)=(√x)(√(1/x)) is correct sgn(−6)=(√(−6))×(√(−(1/6)))=−1 (and not 1) (√(−6))=i(√6) (√(−(1/6)))=i(1/(√6))

$$\mathrm{sgn}\left({x}\right)=\sqrt{{x}}\sqrt{\frac{\mathrm{1}}{{x}}}\:\mathrm{is}\:\mathrm{correct} \\ $$$$\mathrm{sgn}\left(−\mathrm{6}\right)=\sqrt{−\mathrm{6}}×\sqrt{−\frac{\mathrm{1}}{\mathrm{6}}}=−\mathrm{1}\:\left(\mathrm{and}\:\mathrm{not}\:\mathrm{1}\right) \\ $$$$\sqrt{−\mathrm{6}}={i}\sqrt{\mathrm{6}} \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{6}}}={i}\frac{\mathrm{1}}{\sqrt{\mathrm{6}}} \\ $$

Answered by 123456 last updated on 19/Nov/15

for a certain things and simetry, read the definition for complex sign :D −−−− curiosity it as generalized to C by/ sgn z=(z/(∣z∣)) this act like a vercsor for complex number also sgn z=e^(−ıarg z) arg 0 is undefined because unlike z=1=e^(2πkı) ,k∈Z (k=0 is principal argument, 0≤θ<2π) z=0=0e^(ıθ) ,∀θ∈R you can pick all angle you want.

$$\mathrm{for}\:\mathrm{a}\:\mathrm{certain}\:\mathrm{things}\:\mathrm{and}\:\mathrm{simetry},\:\mathrm{read} \\ $$$$\mathrm{the}\:\mathrm{definition}\:\mathrm{for}\:\mathrm{complex}\:\mathrm{sign}\::\mathrm{D} \\ $$$$−−−−\:\mathrm{curiosity} \\ $$$$\mathrm{it}\:\mathrm{as}\:\mathrm{generalized}\:\mathrm{to}\:\mathbb{C}\:\mathrm{by}/ \\ $$$$\mathrm{sgn}\:{z}=\frac{{z}}{\mid{z}\mid} \\ $$$$\mathrm{this}\:\mathrm{act}\:\mathrm{like}\:\mathrm{a}\:\mathrm{vercsor}\:\mathrm{for}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\mathrm{also} \\ $$$$\mathrm{sgn}\:{z}={e}^{−\imath\mathrm{arg}\:{z}} \\ $$$$\mathrm{arg}\:\mathrm{0}\:\mathrm{is}\:\mathrm{undefined}\:\mathrm{because}\:\mathrm{unlike} \\ $$$${z}=\mathrm{1}={e}^{\mathrm{2}\pi{k}\imath} ,{k}\in\mathbb{Z}\:\left({k}=\mathrm{0}\:\mathrm{is}\:\mathrm{principal}\:\mathrm{argument},\:\mathrm{0}\leqslant\theta<\mathrm{2}\pi\right) \\ $$$${z}=\mathrm{0}=\mathrm{0}{e}^{\imath\theta} ,\forall\theta\in\mathbb{R} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{pick}\:\mathrm{all}\:\mathrm{angle}\:\mathrm{you}\:\mathrm{want}. \\ $$

Commented by Rasheed Soomro last updated on 19/Nov/15

I didn′t understand somethings: •this act like a vercsor for complex number What is vercsor? •also if you take arg 0=0(wich is undefined) its flows natural What does this mean? Overall the coment is knowledge−increasing. The idea of generalization of sign to comlex numbers is inspiring!

$${I}\:{didn}'{t}\:{understand}\:{somethings}: \\ $$$$\bullet\mathrm{this}\:\mathrm{act}\:\mathrm{like}\:\mathrm{a}\:\mathrm{vercsor}\:\mathrm{for}\:\mathrm{complex}\:\mathrm{number} \\ $$$${What}\:{is}\:\mathrm{vercsor}? \\ $$$$\bullet\mathrm{also}\:\mathrm{if}\:\mathrm{you}\:\mathrm{take}\:\mathrm{arg}\:\mathrm{0}=\mathrm{0}\left(\mathrm{wich}\:\mathrm{is}\:\mathrm{undefined}\right) \\ $$$$\mathrm{its}\:\mathrm{flows}\:\mathrm{natural}\:\:\:{What}\:{does}\:{this}\:{mean}? \\ $$$$\mathcal{O}{verall}\:{the}\:{coment}\:{is}\:{knowledge}−{increasing}. \\ $$$${The}\:{idea}\:{of}\:{generalization}\:{of}\:{sign}\:{to}\:{comlex}\: \\ $$$${numbers}\:{is}\:{inspiring}! \\ $$

Commented by Filup last updated on 19/Nov/15

What is arg(z)? I′ve seen it before

$$\mathrm{What}\:\mathrm{is}\:\mathrm{arg}\left({z}\right)? \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{seen}\:\mathrm{it}\:\mathrm{before} \\ $$

Commented by 123456 last updated on 19/Nov/15

the argument of the complex number if you consider the complex a vector it is the angle of it and the real axis

$$\mathrm{the}\:\mathrm{argument}\:\mathrm{of}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{a}\:\mathrm{vector} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{it}\:\mathrm{and}\:\mathrm{the}\:\mathrm{real}\:\mathrm{axis} \\ $$

Commented by Filup last updated on 19/Nov/15

I see. I haven′t leant much on the complex plane, so this interests me. I′ll have to take a look at complex mathematics!

$$\mathrm{I}\:\mathrm{see}.\:\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{leant}\:\mathrm{much}\:\mathrm{on}\:\mathrm{the}\:\mathrm{complex} \\ $$$$\mathrm{plane},\:\mathrm{so}\:\mathrm{this}\:\mathrm{interests}\:\mathrm{me}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{have}\:\mathrm{to} \\ $$$$\mathrm{take}\:\mathrm{a}\:\mathrm{look}\:\mathrm{at}\:\mathrm{complex}\:\mathrm{mathematics}! \\ $$

Commented by Rasheed Soomro last updated on 19/Nov/15

THank^S

$$\mathcal{TH}{ank}^{\mathcal{S}} \\ $$

Commented by 123456 last updated on 19/Nov/15

vecsor is a vector with unitary module its ussefull if you want only the direction of a thing f_g =G((m_1 m_2 )/(∣r_(12) ^→ ∣))r_(12) ^� the vecsor r_(12) ^� only give the direction, this is the gravitational force into body 1 for the segund thinked wrong XD sorry for that

$$\mathrm{vecsor}\:\mathrm{is}\:\mathrm{a}\:\mathrm{vector}\:\mathrm{with}\:\mathrm{unitary}\:\mathrm{module} \\ $$$$\mathrm{its}\:\mathrm{ussefull}\:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{only}\:\mathrm{the}\:\mathrm{direction} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{thing} \\ $$$$\mathrm{f}_{\mathrm{g}} =\mathrm{G}\frac{{m}_{\mathrm{1}} {m}_{\mathrm{2}} }{\mid\overset{\rightarrow} {{r}}_{\mathrm{12}} \mid}\hat {{r}}_{\mathrm{12}} \\ $$$$\mathrm{the}\:\mathrm{vecsor}\:\hat {{r}}_{\mathrm{12}} \:\mathrm{only}\:\mathrm{give}\:\mathrm{the}\:\mathrm{direction}, \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{gravitational}\:\mathrm{force}\:\mathrm{into}\:\mathrm{body} \\ $$$$\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{segund}\:\:\mathrm{thinked}\:\mathrm{wrong}\:\mathrm{XD} \\ $$$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{that} \\ $$

Commented by Rasheed Soomro last updated on 20/Nov/15

I want to understand clearly: If z=a+ib then sgn(a+ib)=((a+ib)/(∣a+ib∣))=(a/(√(a^2 +b^2 )))+((ib)/(√(a^2 +b^2 ))) Clearly all z having same ∣z∣ have same sgn(z)! Do all complex numbers having same absolute value have same sign?

$${I}\:{want}\:{to}\:{understand}\:{clearly}: \\ $$$${If}\:{z}={a}+{ib}\:{then} \\ $$$${sgn}\left({a}+{ib}\right)=\frac{{a}+{ib}}{\mid{a}+{ib}\mid}=\frac{{a}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}+\frac{{ib}}{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${Clearly}\:\:{all}\:{z}\:{having}\:{same}\:\mid{z}\mid\:{have}\:{same}\:{sgn}\left({z}\right)! \\ $$$${Do}\:{all}\:{complex}\:{numbers}\:{having}\:{same}\:{absolute}\:{value} \\ $$$${have}\:{same}\:{sign}? \\ $$

Commented by Filup last updated on 20/Nov/15

Absolute Value z_1 =a_1 +b_1 i ∣ z_2 =a_2 +b_2 i ∣z_1 ∣=(√(a_1 ^2 +b_1 ^2 )) ∣ ∣z_2 ∣=(√(a_2 ^2 +b_2 ^2 )) ∣z_1 ∣≥0 ∣ ∣z_2 ∣≥0 assume ∣z_1 ∣=∣z_2 ∣ Sign sgn(z_1 )=e^(i arg(z_1 )) sgn(z_2 )=e^(i arg(z_2 )) if when complex functions with equal abs. values are equal, the sgn are equal, then: for ∣z_1 ∣=∣z_2 ∣ e^(i arg(z_1 )) =e^(i arg(z_2 )) ∴arg(z_1 )=arg(z_2 ) arg(a_1 +b_1 i)=arg(a_2 +b_2 i) (?)

$${Absolute}\:{Value} \\ $$$${z}_{\mathrm{1}} ={a}_{\mathrm{1}} +{b}_{\mathrm{1}} {i}\:\:\:\:\mid\:\:\:\:{z}_{\mathrm{2}} ={a}_{\mathrm{2}} +{b}_{\mathrm{2}} {i} \\ $$$$\mid{z}_{\mathrm{1}} \mid=\sqrt{{a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} }\:\:\:\:\mid\:\:\:\:\mid{z}_{\mathrm{2}} \mid=\sqrt{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\mid{z}_{\mathrm{1}} \mid\geqslant\mathrm{0}\:\:\:\:\mid\:\:\:\:\mid{z}_{\mathrm{2}} \mid\geqslant\mathrm{0} \\ $$$${assume}\:\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid \\ $$$$ \\ $$$$\mathrm{S}{ign} \\ $$$$\mathrm{sgn}\left({z}_{\mathrm{1}} \right)={e}^{{i}\:\mathrm{arg}\left({z}_{\mathrm{1}} \right)} \\ $$$$\mathrm{sgn}\left({z}_{\mathrm{2}} \right)={e}^{{i}\:\mathrm{arg}\left({z}_{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{when}\:\mathrm{complex}\:\mathrm{functions}\:\mathrm{with}\:\mathrm{equal}\:\mathrm{abs}.\:\mathrm{values} \\ $$$$\mathrm{are}\:\mathrm{equal},\:\mathrm{the}\:\mathrm{sgn}\:\mathrm{are}\:\mathrm{equal},\:{then}: \\ $$$$ \\ $$$${for}\:\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid \\ $$$${e}^{{i}\:\mathrm{arg}\left({z}_{\mathrm{1}} \right)} ={e}^{{i}\:\mathrm{arg}\left({z}_{\mathrm{2}} \right)} \\ $$$$\therefore\mathrm{arg}\left({z}_{\mathrm{1}} \right)=\mathrm{arg}\left({z}_{\mathrm{2}} \right) \\ $$$$\mathrm{arg}\left({a}_{\mathrm{1}} +{b}_{\mathrm{1}} {i}\right)=\mathrm{arg}\left({a}_{\mathrm{2}} +{b}_{\mathrm{2}} {i}\right) \\ $$$$\left(?\right) \\ $$

Commented by 123456 last updated on 20/Nov/15

z_1 and z_2 have same sign only if ∃λ∈R,0<λ<+∞ such that z_2 =λz_1

$${z}_{\mathrm{1}} \:\mathrm{and}\:{z}_{\mathrm{2}} \:\mathrm{have}\:\mathrm{same}\:\mathrm{sign}\:\mathrm{only}\:\mathrm{if} \\ $$$$\exists\lambda\in\mathbb{R},\mathrm{0}<\lambda<+\infty\:\mathrm{such}\:\mathrm{that} \\ $$$${z}_{\mathrm{2}} =\lambda{z}_{\mathrm{1}} \\ $$

Commented by prakash jain last updated on 20/Nov/15

z_1 =a_1 +ib_1 arg (z)=arctan(a_1 ,b_1 ) Individual sign of a_1 and b_1 are important. On Rasheed′s comment all z having the same ∣z∣ does not mean same sgn(z) z_1 =3+4i, z_2 =4+3i sgn(z_1 )=.6+.8i, sgn(z_2 )=.8+.6i

$${z}_{\mathrm{1}} ={a}_{\mathrm{1}} +{ib}_{\mathrm{1}} \\ $$$$\mathrm{arg}\:\left({z}\right)=\mathrm{arctan}\left({a}_{\mathrm{1}} ,{b}_{\mathrm{1}} \right) \\ $$$$\mathrm{Individual}\:\mathrm{sign}\:\mathrm{of}\:{a}_{\mathrm{1}} \:\mathrm{and}\:{b}_{\mathrm{1}} \mathrm{are}\:\mathrm{important}. \\ $$$$\mathrm{On}\:\mathrm{Rasheed}'\mathrm{s}\:\mathrm{comment} \\ $$$$\mathrm{all}\:{z}\:\mathrm{having}\:\mathrm{the}\:\mathrm{same}\:\mid{z}\mid\:\mathrm{does}\:\mathrm{not}\:\mathrm{mean} \\ $$$$\mathrm{same}\:\mathrm{sgn}\left({z}\right) \\ $$$${z}_{\mathrm{1}} =\mathrm{3}+\mathrm{4}{i},\:{z}_{\mathrm{2}} =\mathrm{4}+\mathrm{3}{i} \\ $$$$\mathrm{sgn}\left({z}_{\mathrm{1}} \right)=.\mathrm{6}+.\mathrm{8}{i},\:\mathrm{sgn}\left({z}_{\mathrm{2}} \right)=.\mathrm{8}+.\mathrm{6}{i} \\ $$

Commented by Rasheed Soomro last updated on 20/Nov/15

THANKS To All of You! I Was In MisUnderstanding.

$$\mathcal{THANKS}\:\:\mathcal{T}{o}\:\mathcal{A}{ll}\:{of}\:\:\mathcal{Y}{ou}!\: \\ $$$$\mathcal{I}\:\:\mathcal{W}{as}\:\:\mathcal{I}{n}\:\mathcal{M}{is}\mathcal{U}{nderstanding}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com