
Question Number 24025 by ajfour last updated on 11/Nov/17

Commented by ajfour last updated on 11/Nov/17

$${Find}\:{the}\:{closest}\:{distance}\:{of} \\ $$$${approach}\:{of}\:{B}\:{and}\:{R}\:\:\left({if}\:{it}\:{is}\right. \\ $$$$\left.{yet}\:{to}\:{come}\right)\:{and}\:{time}\:{after} \\ $$$${which}\:{they}\:{are}\:{closest}. \\ $$$${Situation}\:{has}\:{been}\:{shown}\:{for} \\ $$$${t}=\mathrm{0}\:.\:\left({Assume}\:{constant}\:{velocities}\right) \\ $$$${B}\:{continues}\:{along}\:{its}\:{road}\:{and} \\ $$$${so}\:{does}\:{R}\:. \\ $$$${B}\:{is}\:{the}\:{blue}\:{vehicle},\:{and}\:{R}\:{the} \\ $$$${red}\:{one},\:{both}\:{roads}\:{are}\:{inclined} \\ $$$${at}\:\angle\:\alpha\:{to}\:{each}\:{other}. \\ $$
Commented by ajfour last updated on 12/Nov/17

Commented by ajfour last updated on 12/Nov/17
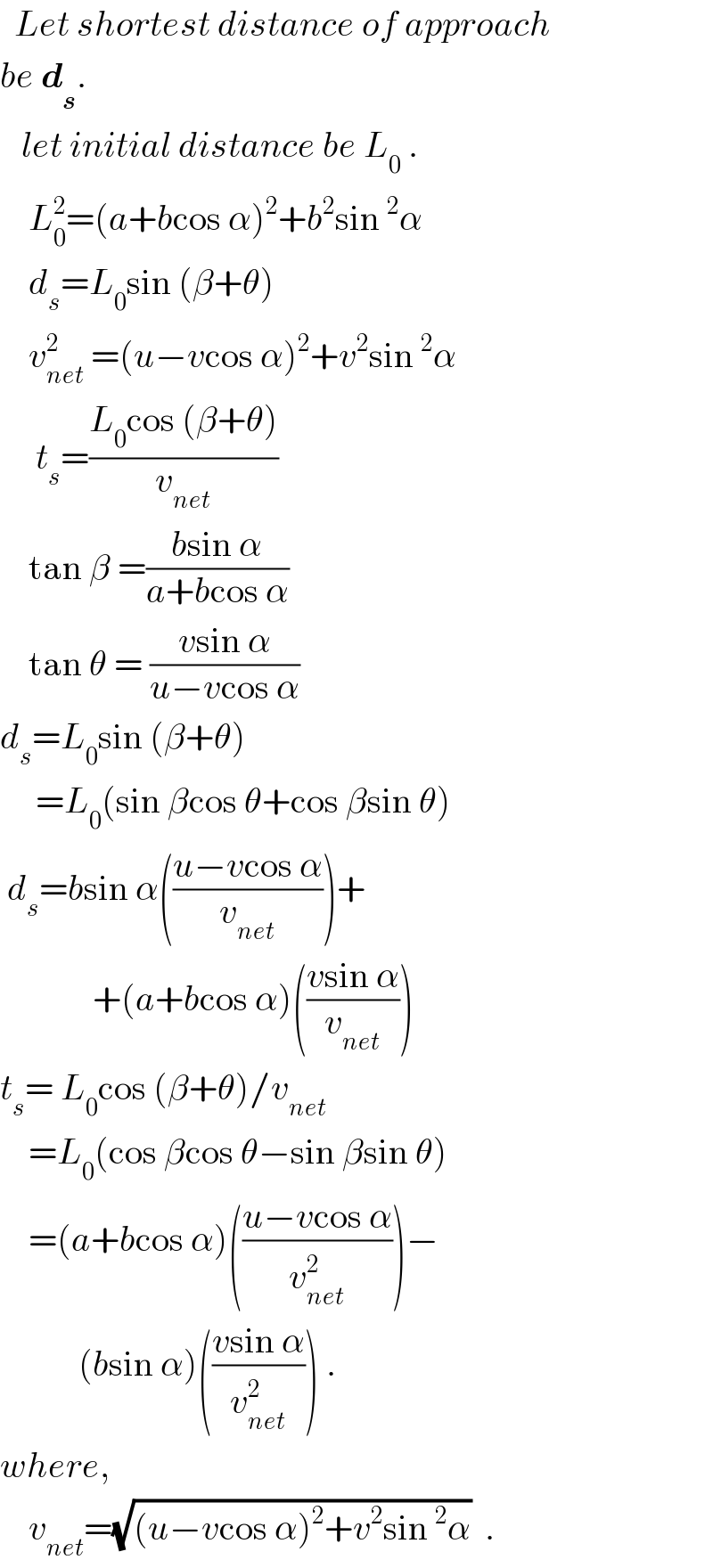
$$\:\:{Let}\:{shortest}\:{distance}\:{of}\:{approach} \\ $$$${be}\:\boldsymbol{{d}}_{\boldsymbol{{s}}} . \\ $$$$\:\:\:{let}\:{initial}\:{distance}\:{be}\:{L}_{\mathrm{0}} \:. \\ $$$$\:\:\:\:{L}_{\mathrm{0}} ^{\mathrm{2}} =\left({a}+{b}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:{d}_{{s}} ={L}_{\mathrm{0}} \mathrm{sin}\:\left(\beta+\theta\right) \\ $$$$\:\:\:\:{v}_{{net}} ^{\mathrm{2}} \:=\left({u}−{v}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\:{t}_{{s}} =\frac{{L}_{\mathrm{0}} \mathrm{cos}\:\left(\beta+\theta\right)}{{v}_{{net}} } \\ $$$$\:\:\:\:\mathrm{tan}\:\beta\:=\frac{{b}\mathrm{sin}\:\alpha}{{a}+{b}\mathrm{cos}\:\alpha} \\ $$$$\:\:\:\:\mathrm{tan}\:\theta\:=\:\frac{{v}\mathrm{sin}\:\alpha}{{u}−{v}\mathrm{cos}\:\alpha}\: \\ $$$${d}_{{s}} ={L}_{\mathrm{0}} \mathrm{sin}\:\left(\beta+\theta\right) \\ $$$$\:\:\:\:\:={L}_{\mathrm{0}} \left(\mathrm{sin}\:\beta\mathrm{cos}\:\theta+\mathrm{cos}\:\beta\mathrm{sin}\:\theta\right) \\ $$$$\:{d}_{{s}} ={b}\mathrm{sin}\:\alpha\left(\frac{{u}−{v}\mathrm{cos}\:\alpha}{{v}_{{net}} }\right)+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\frac{{v}\mathrm{sin}\:\alpha}{{v}_{{net}} }\right)\: \\ $$$${t}_{{s}} =\:{L}_{\mathrm{0}} \mathrm{cos}\:\left(\beta+\theta\right)/{v}_{{net}} \\ $$$$\:\:\:\:={L}_{\mathrm{0}} \left(\mathrm{cos}\:\beta\mathrm{cos}\:\theta−\mathrm{sin}\:\beta\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:=\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\frac{{u}−{v}\mathrm{cos}\:\alpha}{{v}_{{net}} ^{\mathrm{2}} }\right)− \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left({b}\mathrm{sin}\:\alpha\right)\left(\frac{{v}\mathrm{sin}\:\alpha}{{v}_{{net}} ^{\mathrm{2}} }\right)\:. \\ $$$${where}, \\ $$$$\:\:\:\:{v}_{{net}} =\sqrt{\left({u}−{v}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha}\:\:. \\ $$
Commented by Physics lover last updated on 12/Nov/17

$${thats}\:{exactly}\:{how}\:{i}\:{thought}. \\ $$
Answered by mrW1 last updated on 12/Nov/17
![at t=0, the distance between B and R: L_0 =(√((a+bcos α)^2 +(bsin α)^2 )) =(√(a^2 +b^2 +2abcos α)) at t: L=(√([a−ut+(b+vt)cos α]^2 +[(b+vt)sin α]^2 )) let D=L^2 D=[a−ut+(b+vt)cos α]^2 +[(b+vt)sin α]^2 =[a+bcos α−(1−cos α)ut]^2 +[bsin α+sin αvt]^2 =(a+bcos α)^2 −2(a+bcos α)(1−cos α)ut+(1−cos α)^2 u^2 t^2 +b^2 sin^2 α+2bsin^2 αvt+sin^2 α v^2 t^2 =[(a+bcos α)^2 +b^2 sin^2 α]−2[u(a+bcos α)(1−cos α)+vbsin^2 α]t+[u^2 (1−cos α)^2 +v^2 sin^2 α]t^2 =[u^2 (1−cos α)^2 +v^2 sin^2 α]t^2 −2[u(a+bcos α)(1−cos α)+vbsin^2 α]t+[a^2 +b^2 +2abcos α] =pt^2 −2qt+r =p(t−(q/p))^2 +(r−(q^2 /p)) since p>0, there is a minimum for D at t=t_m =(q/p)=((u(a+bcos α)(1−cos α)+vbsin^2 α)/(u^2 (1−cos α)^2 +v^2 sin^2 α)) D_(min) =r−(q^2 /p) =[a^2 +b^2 +2abcos α]−(([u(a+bcos α)(1−cos α)+vbsin^2 α]^2 )/(u^2 (1−cos α)^2 +v^2 sin^2 α)) L_(min) =(√([a^2 +b^2 +2abcos α]−(([u(a+bcos α)(1−cos α)+vbsin^2 α]^2 )/(u^2 (1−cos α)^2 +v^2 sin^2 α))))](Q24070.png)
$${at}\:{t}=\mathrm{0},\:{the}\:{distance}\:{between}\:{B}\:{and}\:{R}: \\ $$$${L}_{\mathrm{0}} =\sqrt{\left({a}+{b}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left({b}\mathrm{sin}\:\alpha\right)^{\mathrm{2}} } \\ $$$$=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\mathrm{cos}\:\alpha} \\ $$$$ \\ $$$${at}\:{t}: \\ $$$${L}=\sqrt{\left[{a}−{ut}+\left({b}+{vt}\right)\mathrm{cos}\:\alpha\right]^{\mathrm{2}} +\left[\left({b}+{vt}\right)\mathrm{sin}\:\alpha\right]^{\mathrm{2}} } \\ $$$${let}\:{D}={L}^{\mathrm{2}} \\ $$$${D}=\left[{a}−{ut}+\left({b}+{vt}\right)\mathrm{cos}\:\alpha\right]^{\mathrm{2}} +\left[\left({b}+{vt}\right)\mathrm{sin}\:\alpha\right]^{\mathrm{2}} \\ $$$$=\left[{a}+{b}\mathrm{cos}\:\alpha−\left(\mathrm{1}−\mathrm{cos}\:\alpha\right){ut}\right]^{\mathrm{2}} +\left[{b}\mathrm{sin}\:\alpha+\mathrm{sin}\:\alpha{vt}\right]^{\mathrm{2}} \\ $$$$=\left({a}+{b}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} −\mathrm{2}\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right){ut}+\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} {u}^{\mathrm{2}} {t}^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+\mathrm{2}{b}\mathrm{sin}^{\mathrm{2}} \:\alpha{vt}+\mathrm{sin}^{\mathrm{2}} \:\alpha\:{v}^{\mathrm{2}} {t}^{\mathrm{2}} \\ $$$$=\left[\left({a}+{b}\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha\right]−\mathrm{2}\left[{u}\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)+{vb}\mathrm{sin}^{\mathrm{2}} \:\alpha\right]{t}+\left[{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha\right]{t}^{\mathrm{2}} \\ $$$$=\left[{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha\right]{t}^{\mathrm{2}} −\mathrm{2}\left[{u}\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)+{vb}\mathrm{sin}^{\mathrm{2}} \:\alpha\right]{t}+\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\mathrm{cos}\:\alpha\right] \\ $$$$={pt}^{\mathrm{2}} −\mathrm{2}{qt}+{r} \\ $$$$={p}\left({t}−\frac{{q}}{{p}}\right)^{\mathrm{2}} +\left({r}−\frac{{q}^{\mathrm{2}} }{{p}}\right) \\ $$$${since}\:{p}>\mathrm{0},\:{there}\:{is}\:{a}\:{minimum}\:{for}\:{D} \\ $$$${at}\:{t}={t}_{{m}} =\frac{{q}}{{p}}=\frac{{u}\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)+{vb}\mathrm{sin}^{\mathrm{2}} \:\alpha}{{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha} \\ $$$${D}_{{min}} ={r}−\frac{{q}^{\mathrm{2}} }{{p}} \\ $$$$=\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\mathrm{cos}\:\alpha\right]−\frac{\left[{u}\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)+{vb}\mathrm{sin}^{\mathrm{2}} \:\alpha\right]^{\mathrm{2}} }{{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha} \\ $$$${L}_{{min}} =\sqrt{\left[{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\mathrm{cos}\:\alpha\right]−\frac{\left[{u}\left({a}+{b}\mathrm{cos}\:\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)+{vb}\mathrm{sin}^{\mathrm{2}} \:\alpha\right]^{\mathrm{2}} }{{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +{v}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha}} \\ $$
Commented by ajfour last updated on 12/Nov/17

$${thank}\:{you}\:{Sir},\:{please}\:{view}\:{my} \\ $$$${solution}\:{sir}\:.. \\ $$
Commented by mrW1 last updated on 14/Nov/17
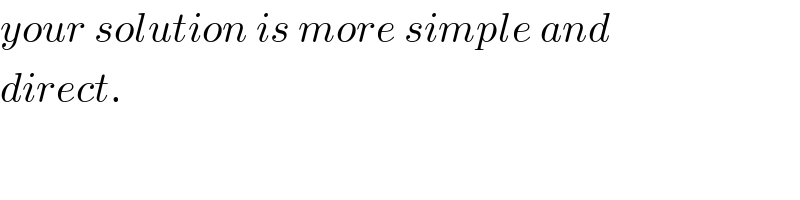
$${your}\:{solution}\:{is}\:{more}\:{simple}\:{and} \\ $$$${direct}. \\ $$
Commented by ajfour last updated on 15/Nov/17

$${thanks}\:{for}\:{the}\:{appreciation},\:{Sir}! \\ $$
