Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 24286 by Joel577 last updated on 15/Nov/17

$$\mathrm{If}\mid x\mid <1\mathrm{then}$$ $$(x+1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1).....$$ $$\mathrm{is}\mathrm{equal}\mathrm{to}$$

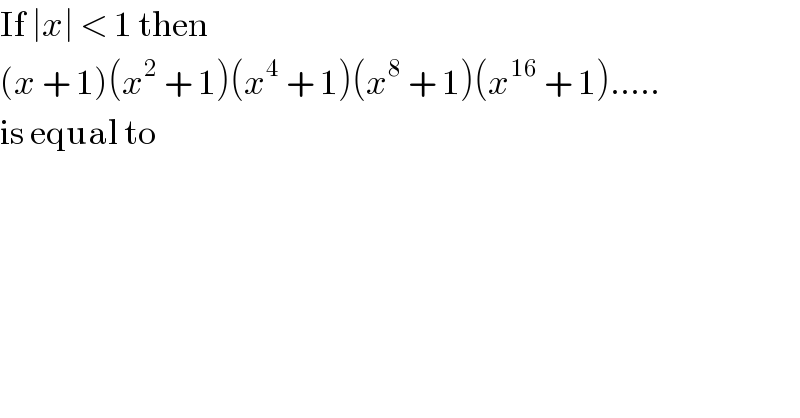
Answered by mrW1 last updated on 15/Nov/17

$$let{P}_n=(x+1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1).....(x^{2^n}+1)$$ $$(x-1)P_n=(x-1)(x+1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1).....(x^{2^n}+1)$$ $$(x-1)P_n=(x^2-1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1).....(x^{2^n}+1)$$ $$(x-1)P_n=(x^4-1)(x^4+1)(x^8+1)(x^{16}+1).....(x^{2^n}+1)$$ $$......$$ $$(x-1)P_n=(x^{2^n}-1)(x^{2^n}+1)$$ $$(x-1)P_n=x^{2^{n+1}}-1$$ $$\Rightarrow P_n=\frac{1-x^{2^{n+1}}}{1-x}$$ $$\underset{n\to \mathrm{\infty }}{\lim }{P}_n=\frac{1}{1-x}$$ $$\Rightarrow (x+1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1).....=\frac{1}{1-x}$$

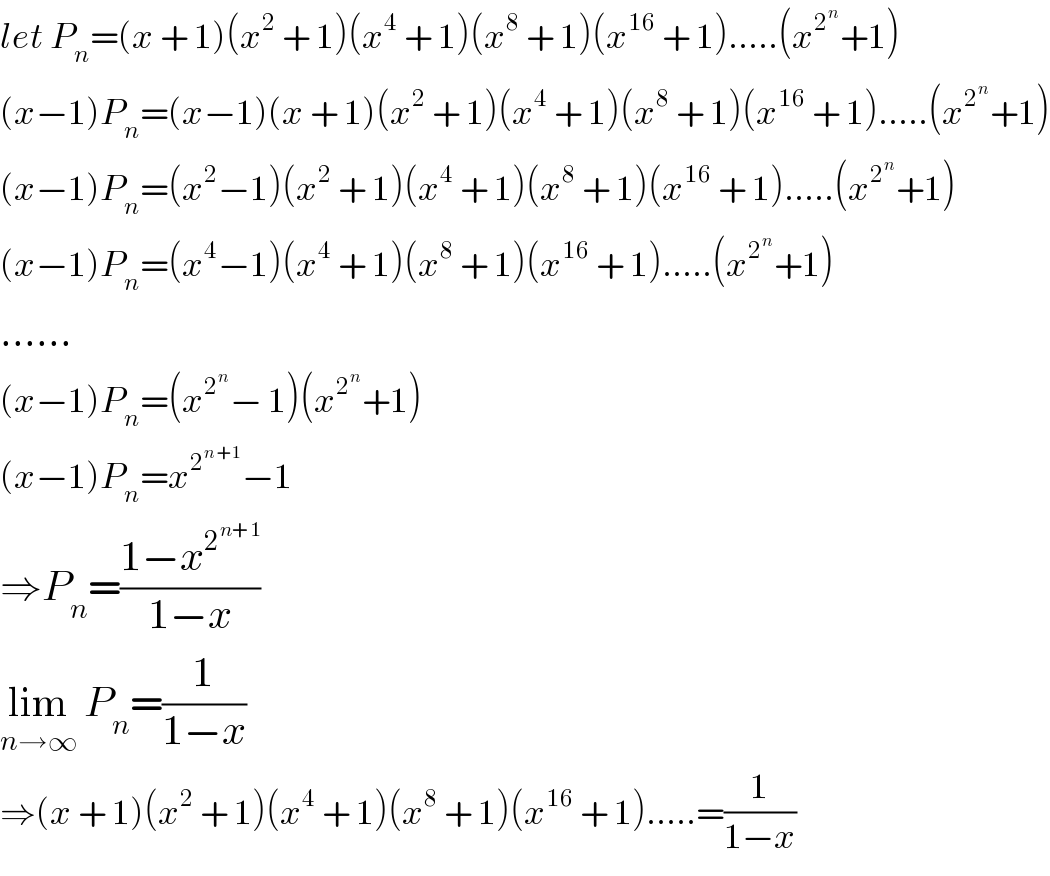
Commented bymath solver last updated on 16/Nov/17

$$\mathrm{sir},\mathrm{can}\mathrm{you}\mathrm{explain}\mathrm{your}\mathrm{last}\mathrm{step}$$ $$\mathrm{when}\mathrm{n}\mathrm{tending}\mathrm{to}\mathrm{infinity}?$$

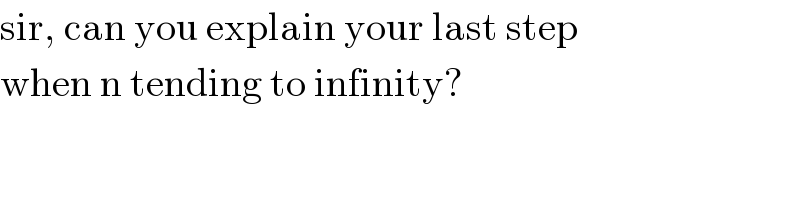
Commented bymrW1 last updated on 16/Nov/17

$$wehave{P}_n=\frac{1-x^{2^{n+1}}}{1-x}$$ $$whenn\to \mathrm{\infty },$$ $$2^{n+1}\to \mathrm{\infty }$$ $$since\mid x\mid <1$$ $$x^{2^{n+1}}\to 0$$ $$P_n\to \frac{1-0}{1-x}=\frac{1}{1-x}$$

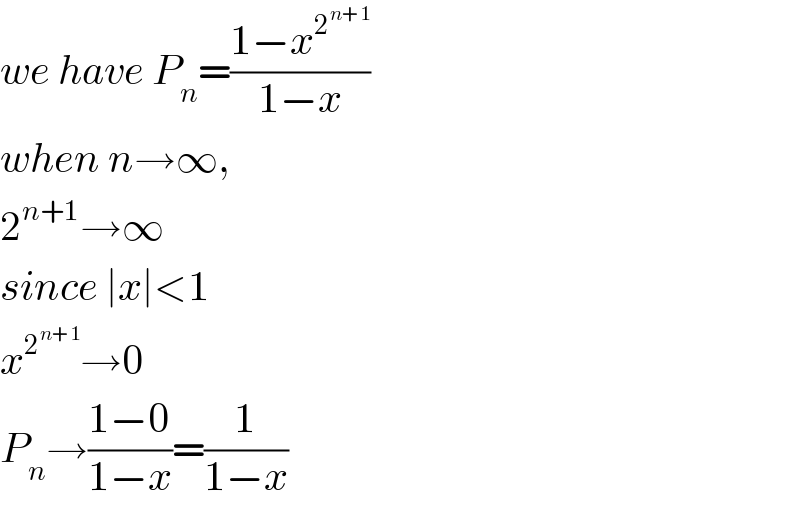
Commented bymath solver last updated on 16/Nov/17

$$\mathrm{okk},\mathrm{i}{\mathrm{didn}}^{\prime }\mathrm{t}\mathrm{read}\mid \mathrm{x}\mid <1.$$

Commented byJoel577 last updated on 16/Nov/17

$$thankyouverymuch$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com