
Question Number 2441 by Yozzi last updated on 20/Nov/15

$${Prove}\:{or}\:{disprove}\:{that}\:,\:{for}\:{even}\: \\ $$$${positive}\:{n}, \\ $$$$\mathrm{2}×\underset{{k}=\mathrm{1}} {\overset{\frac{{n}}{\mathrm{2}}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}+\left(−\mathrm{1}\right)^{\left({n}/\mathrm{2}\right)} \frac{{n}!}{\left(\left({n}/\mathrm{2}\right)!\right)^{\mathrm{2}} }=−\mathrm{2} \\ $$
Commented by Rasheed Soomro last updated on 20/Nov/15
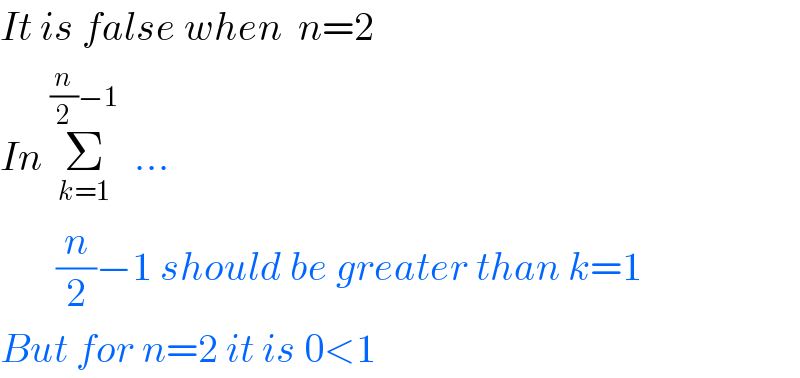
$${It}\:{is}\:{false}\:{when}\:\:{n}=\mathrm{2} \\ $$$${In}\:\underset{{k}=\mathrm{1}} {\overset{\frac{{n}}{\mathrm{2}}−\mathrm{1}} {\sum}}\:\:... \\ $$$$\:\:\:\:\:\:\:\frac{{n}}{\mathrm{2}}−\mathrm{1}\:{should}\:{be}\:{greater}\:{than}\:{k}=\mathrm{1} \\ $$$${But}\:{for}\:{n}=\mathrm{2}\:{it}\:{is}\:\mathrm{0}<\mathrm{1} \\ $$
Commented by Yozzi last updated on 20/Nov/15
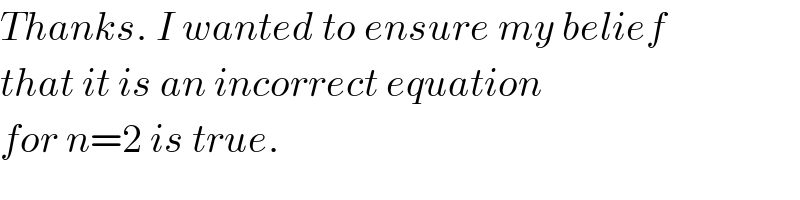
$${Thanks}.\:{I}\:{wanted}\:{to}\:{ensure}\:{my}\:{belief} \\ $$$${that}\:{it}\:{is}\:{an}\:{incorrect}\:{equation} \\ $$$${for}\:{n}=\mathrm{2}\:{is}\:{true}. \\ $$
Commented by prakash jain last updated on 20/Nov/15
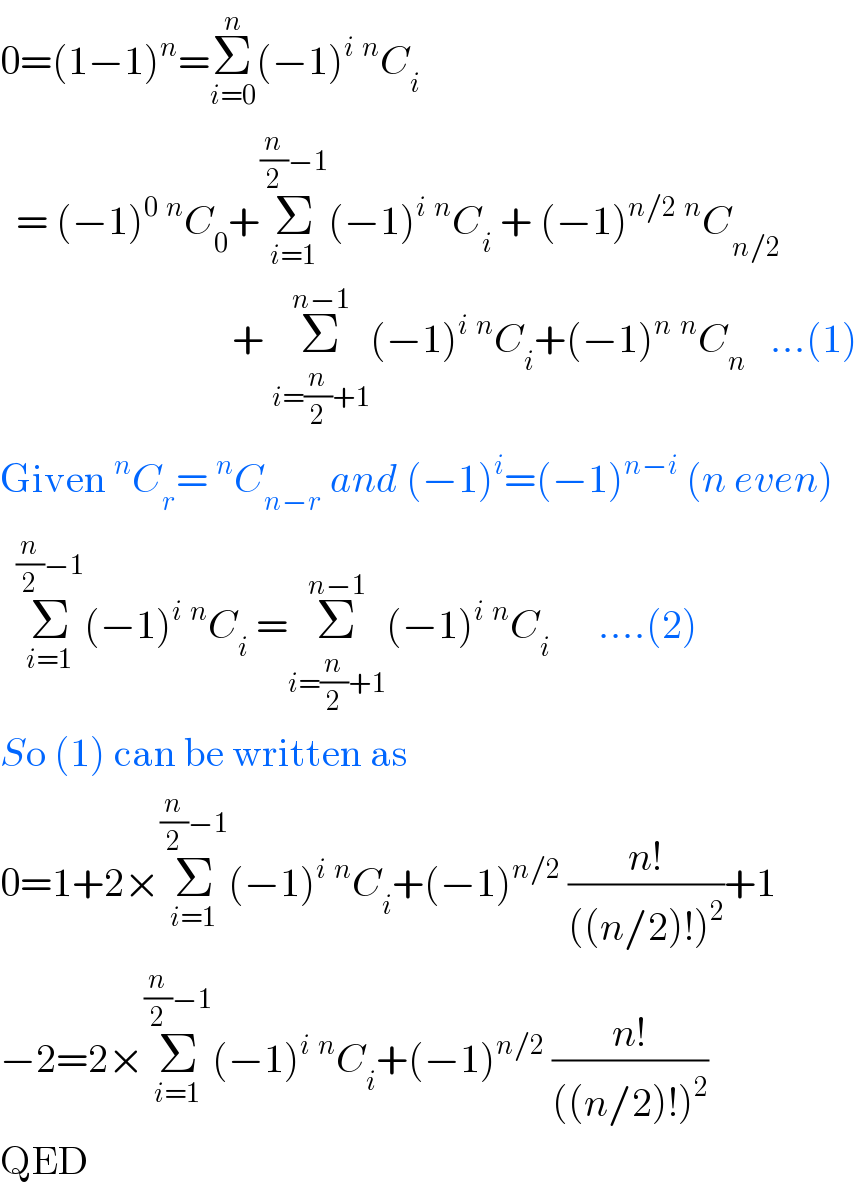
$$\mathrm{0}=\left(\mathrm{1}−\mathrm{1}\right)^{{n}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} \\ $$$$\:\:=\:\left(−\mathrm{1}\right)^{\mathrm{0}} \:^{{n}} {C}_{\mathrm{0}} +\underset{{i}=\mathrm{1}} {\overset{\frac{{n}}{\mathrm{2}}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} \:+\:\left(−\mathrm{1}\right)^{{n}/\mathrm{2}} \:^{{n}} {C}_{{n}/\mathrm{2}} \: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\underset{{i}=\frac{{n}}{\mathrm{2}}+\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} +\left(−\mathrm{1}\right)^{{n}} \:^{{n}} {C}_{{n}} \:\:\:...\left(\mathrm{1}\right) \\ $$$$\mathrm{Given}\:^{{n}} {C}_{{r}} =\:^{{n}} {C}_{{n}−{r}} \:{and}\:\left(−\mathrm{1}\right)^{{i}} =\left(−\mathrm{1}\right)^{{n}−{i}} \:\left({n}\:{even}\right) \\ $$$$\:\:\underset{{i}=\mathrm{1}} {\overset{\frac{{n}}{\mathrm{2}}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} \:=\underset{{i}=\frac{{n}}{\mathrm{2}}+\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} \:\:\:\:\:\:....\left(\mathrm{2}\right) \\ $$$${S}\mathrm{o}\:\left(\mathrm{1}\right)\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$$\mathrm{0}=\mathrm{1}+\mathrm{2}×\underset{{i}=\mathrm{1}} {\overset{\frac{{n}}{\mathrm{2}}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} +\left(−\mathrm{1}\right)^{{n}/\mathrm{2}} \:\frac{{n}!}{\left(\left({n}/\mathrm{2}\right)!\right)^{\mathrm{2}} }+\mathrm{1} \\ $$$$−\mathrm{2}=\mathrm{2}×\underset{{i}=\mathrm{1}} {\overset{\frac{{n}}{\mathrm{2}}−\mathrm{1}} {\sum}}\left(−\mathrm{1}\right)^{{i}} \:^{{n}} {C}_{{i}} +\left(−\mathrm{1}\right)^{{n}/\mathrm{2}} \:\frac{{n}!}{\left(\left({n}/\mathrm{2}\right)!\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{QED} \\ $$
Answered by prakash jain last updated on 20/Nov/15
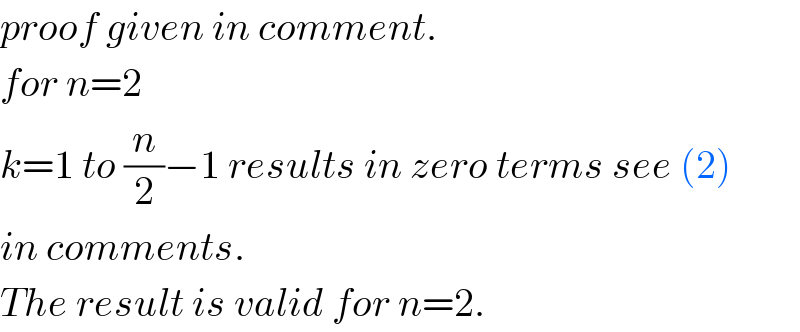
$${proof}\:{given}\:{in}\:{comment}. \\ $$$${for}\:{n}=\mathrm{2} \\ $$$${k}=\mathrm{1}\:{to}\:\frac{{n}}{\mathrm{2}}−\mathrm{1}\:{results}\:{in}\:{zero}\:{terms}\:{see}\:\left(\mathrm{2}\right) \\ $$$${in}\:{comments}. \\ $$$${The}\:{result}\:{is}\:{valid}\:{for}\:{n}=\mathrm{2}. \\ $$
