
Question Number 24477 by sushmitak last updated on 18/Nov/17

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{moving}\:\mathrm{horizonatally} \\ $$$$\mathrm{collides}\:\mathrm{perpendiculrly}\:\mathrm{at}\:\mathrm{one}\:\mathrm{end} \\ $$$$\mathrm{of}\:\:\mathrm{a}\:\mathrm{rod}\:\mathrm{having}\:\mathrm{equal}\:\mathrm{mass}\:\mathrm{and} \\ $$$$\mathrm{placed}\:\mathrm{on}\:\mathrm{a}\:\mathrm{horizontal}\:\mathrm{surface}. \\ $$$$\mathrm{The}\:\mathrm{book}\:\mathrm{says}\:\mathrm{that}\:\mathrm{particle}\:\mathrm{will} \\ $$$$\mathrm{continue}\:\mathrm{to}\:\mathrm{move}\:\mathrm{along}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{direction}\:\mathrm{regardless}\:\mathrm{of}\:\mathrm{value}\:\mathrm{of} \\ $$$${e}\:\left(\mathrm{coefficient}\:\mathrm{of}\:\mathrm{restitution}\right). \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{logic}. \\ $$$$\mathrm{please}\:\mathrm{help}. \\ $$
Commented by sushmitak last updated on 18/Nov/17

Commented by sushmitak last updated on 18/Nov/17

$$\mathrm{My}\:\mathrm{work}\:\mathrm{so}\:\mathrm{far} \\ $$$$\mathrm{initial}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{ball}\:{u} \\ $$$$\mathrm{final}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{ball}\:{v}_{\mathrm{1}} \\ $$$$\mathrm{velocity}\:\mathrm{of}\:\mathrm{center}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{rod}\:{v}_{\mathrm{2}} \\ $$$$\mathrm{angular}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{rod}\:\mathrm{at}\:\mathrm{CM}=\omega \\ $$$${e}=\mathrm{1} \\ $$$${v}={v}_{\mathrm{1}} +{v}_{\mathrm{2}} \\ $$$${angular}\:{momentum}\:{at}\:{CM} \\ $$$${mu}\frac{{l}}{\mathrm{2}}={mv}_{\mathrm{1}} \frac{{l}}{\mathrm{2}}+{Iw}={mv}_{\mathrm{1}} \frac{{l}}{\mathrm{2}}+{m}\frac{{l}^{\mathrm{2}} }{\mathrm{12}}\omega \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mu}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{mv}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{mv}_{\mathrm{2}} ^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} \\ $$$$\mathrm{Are}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{correct}? \\ $$$$\mathrm{thnls}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help} \\ $$
Answered by mrW1 last updated on 19/Nov/17

Commented by mrW1 last updated on 19/Nov/17
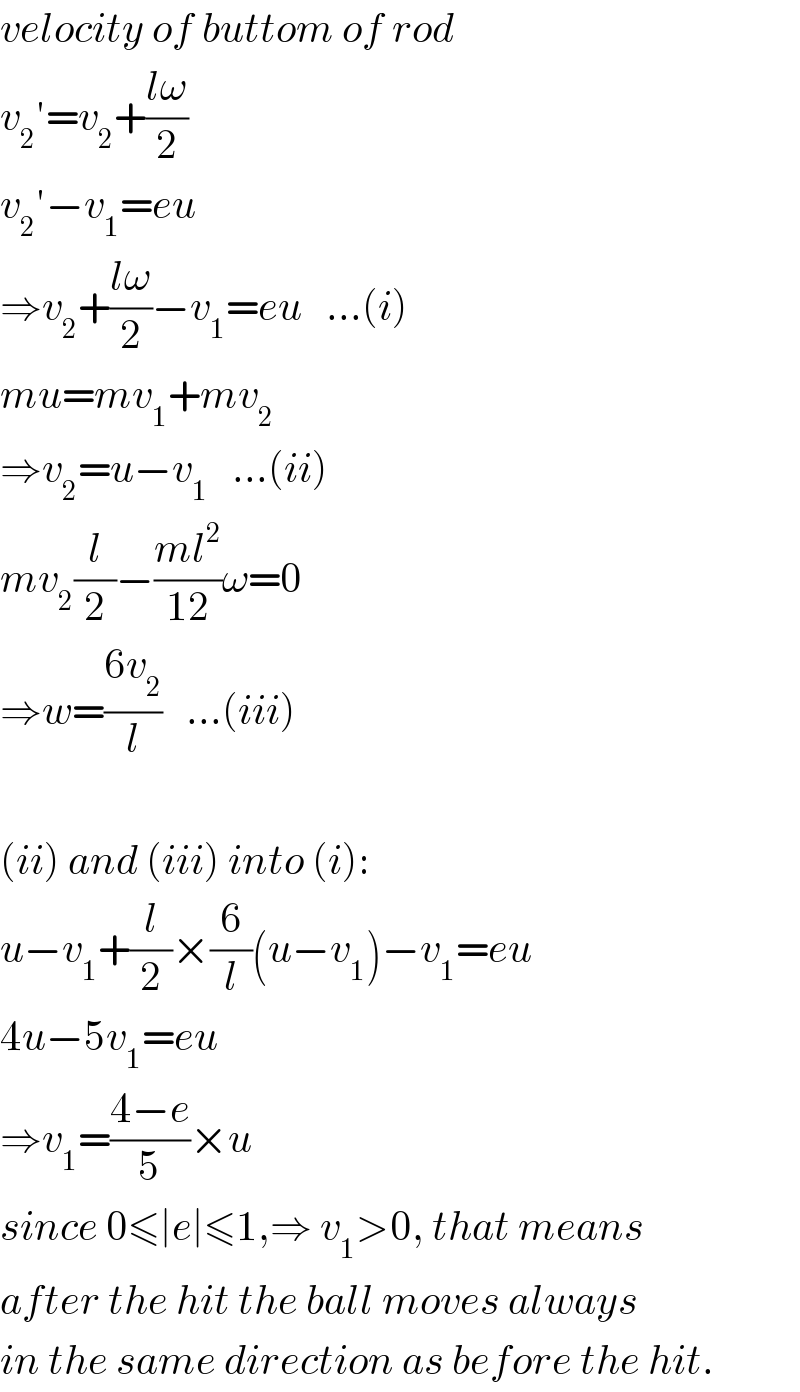
$${velocity}\:{of}\:{buttom}\:{of}\:{rod} \\ $$$${v}_{\mathrm{2}} '={v}_{\mathrm{2}} +\frac{{l}\omega}{\mathrm{2}} \\ $$$${v}_{\mathrm{2}} '−{v}_{\mathrm{1}} ={eu} \\ $$$$\Rightarrow{v}_{\mathrm{2}} +\frac{{l}\omega}{\mathrm{2}}−{v}_{\mathrm{1}} ={eu}\:\:\:...\left({i}\right) \\ $$$${mu}={mv}_{\mathrm{1}} +{mv}_{\mathrm{2}} \\ $$$$\Rightarrow{v}_{\mathrm{2}} ={u}−{v}_{\mathrm{1}} \:\:\:...\left({ii}\right) \\ $$$${mv}_{\mathrm{2}} \frac{{l}}{\mathrm{2}}−\frac{{ml}^{\mathrm{2}} }{\mathrm{12}}\omega=\mathrm{0} \\ $$$$\Rightarrow{w}=\frac{\mathrm{6}{v}_{\mathrm{2}} }{{l}}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$$\left({ii}\right)\:{and}\:\left({iii}\right)\:{into}\:\left({i}\right): \\ $$$${u}−{v}_{\mathrm{1}} +\frac{{l}}{\mathrm{2}}×\frac{\mathrm{6}}{{l}}\left({u}−{v}_{\mathrm{1}} \right)−{v}_{\mathrm{1}} ={eu} \\ $$$$\mathrm{4}{u}−\mathrm{5}{v}_{\mathrm{1}} ={eu} \\ $$$$\Rightarrow{v}_{\mathrm{1}} =\frac{\mathrm{4}−{e}}{\mathrm{5}}×{u} \\ $$$${since}\:\mathrm{0}\leqslant\mid{e}\mid\leqslant\mathrm{1},\Rightarrow\:{v}_{\mathrm{1}} >\mathrm{0},\:{that}\:{means} \\ $$$${after}\:{the}\:{hit}\:{the}\:{ball}\:{moves}\:{always} \\ $$$${in}\:{the}\:{same}\:{direction}\:{as}\:{before}\:{the}\:{hit}. \\ $$
Commented by mrW1 last updated on 19/Nov/17

