Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2454 by Yozzi last updated on 20/Nov/15

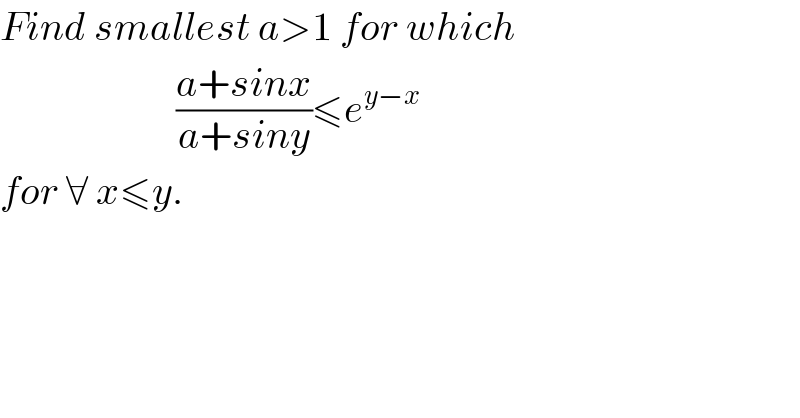
Find smallest a>1 for which ((a+sinx)/(a+siny))≤e^(y−x) for ∀ x≤y.

$${Find}\:{smallest}\:{a}>\mathrm{1}\:{for}\:{which} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}+{sinx}}{{a}+{siny}}\leqslant{e}^{{y}−{x}} \\ $$ $${for}\:\forall\:{x}\leqslant{y}. \\ $$

Commented byRasheed Soomro last updated on 21/Nov/15

Find smallest a>1 for which ((a+sinx)/(a+siny))≤e^(y−x) for ∀ x≤y. −−−−−−−−−−− ((a+sin x)/(a+sin y))≤e^(y−x) a+sin x≤e^(y−x) (a+sin y) ≤ae^(y−x) +e^(y−x) sin y a−ae^(y−x) ≤e^(y−x) sin y −sin x a(1−e^(y−x) )≤e^(y−x) sin y −sin x a≤((e^(y−x) sin y −sin x)/(1−e^(y−x) )) assuming y>x [for y=x see sec A] Since a>1 1<a≤((e^(y−x) sin y −sin x)/(1−e^(y−x) )) a=Smallest ((e^(y−x) sin y −sin x)/(1−e^(y−x) ))>1 We have to use such values of x and y for which_(−) ((e^(y−x) sin y −sin x)/(1−e^(y−x) )) is smallest but greater than 1_(−) For y=x............................section A ((a+sinx)/(a+siny))≤e^(y−x) ((a+sin x)/(a+sin x))≤e^(x−x) 1≤1 No help for a Continue

$${Find}\:{smallest}\:{a}>\mathrm{1}\:{for}\:{which} \\ $$ $$\:\frac{{a}+{sinx}}{{a}+{siny}}\leqslant{e}^{{y}−{x}} \\ $$ $${for}\:\forall\:{x}\leqslant{y}. \\ $$ $$−−−−−−−−−−− \\ $$ $$\:\frac{{a}+{sin}\:{x}}{{a}+{sin}\:{y}}\leqslant{e}^{{y}−{x}} \\ $$ $${a}+{sin}\:{x}\leqslant{e}^{{y}−{x}} \left({a}+{sin}\:{y}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant{ae}^{{y}−{x}} +{e}^{{y}−{x}} {sin}\:{y} \\ $$ $${a}−{ae}^{{y}−{x}} \leqslant{e}^{{y}−{x}} {sin}\:{y}\:−{sin}\:{x} \\ $$ $${a}\left(\mathrm{1}−{e}^{{y}−{x}} \right)\leqslant{e}^{{y}−{x}} {sin}\:{y}\:−{sin}\:{x} \\ $$ $${a}\leqslant\frac{{e}^{{y}−{x}} {sin}\:{y}\:−{sin}\:{x}}{\mathrm{1}−{e}^{{y}−{x}} }\:\:\:\:\:\:{assuming}\:{y}>{x}\:\left[{for}\:{y}={x}\:{see}\:{sec}\:{A}\right] \\ $$ $${Since}\:{a}>\mathrm{1} \\ $$ $$\mathrm{1}<{a}\leqslant\frac{{e}^{{y}−{x}} {sin}\:{y}\:−{sin}\:{x}}{\mathrm{1}−{e}^{{y}−{x}} } \\ $$ $${a}={Smallest}\:\frac{{e}^{{y}−{x}} {sin}\:{y}\:−{sin}\:{x}}{\mathrm{1}−{e}^{{y}−{x}} }>\mathrm{1} \\ $$ $$\underset{−} {{We}\:{have}\:{to}\:{use}\:{such}\:{values}\:{of}\:{x}\:{and}\:{y}\:{for}\:{which}} \\ $$ $$\underset{−} {\frac{{e}^{{y}−{x}} {sin}\:{y}\:−{sin}\:{x}}{\mathrm{1}−{e}^{{y}−{x}} }\:{is}\:{smallest}\:{but}\:{greater}\:{than}\:\mathrm{1}} \\ $$ $${For}\:{y}={x}............................{section}\:{A} \\ $$ $$\:\frac{{a}+{sinx}}{{a}+{siny}}\leqslant{e}^{{y}−{x}} \\ $$ $$\:\frac{{a}+{sin}\:{x}}{{a}+{sin}\:{x}}\leqslant{e}^{{x}−{x}} \\ $$ $$\mathrm{1}\leqslant\mathrm{1}\:\:\:\:{No}\:{help}\:{for}\:{a} \\ $$ $${Continue} \\ $$

Commented byprakash jain last updated on 20/Nov/15

Since a>1, a+sin y>0 and e^x >0 we can rewrite the inequality as f(x,y)=ae^x +e^x sin x−(ae^y +e^y sin y) For f(x,y) ≤0, we need to chose a such that value at maxima is 0. f_x =ae^x +e^x sin x+e^x cos x f_y =−(ae^y +e^x sin y+e^x cos y) function f will attain maxima or minima when f_x and f_y are both 0. f_x =0⇒e^x (a+sin x+cos x)=0 a+(√2)sin (x+(π/4))=0 similarly a+(√2)sin (y+(π/4))=0 The critical points are given by: x=2πn+2tan^(−1) (((−(√(2−a^2 ))−1)/(a−1))), n∈Z y=2πm+2tan^(−1) (((−(√(2−a^2 ))−1)/(a−1))), m∈Z The problem statement is to chose a such that f(x,y)≤0 at critical points. To be continued in answer.

$$\mathrm{Since}\:{a}>\mathrm{1},\:{a}+\mathrm{sin}\:{y}>\mathrm{0}\:{and}\:{e}^{{x}} >\mathrm{0} \\ $$ $$\mathrm{we}\:\mathrm{can}\:\mathrm{rewrite}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{as} \\ $$ $${f}\left({x},{y}\right)={ae}^{{x}} +{e}^{{x}} \mathrm{sin}\:{x}−\left({ae}^{{y}} +{e}^{{y}} \mathrm{sin}\:{y}\right) \\ $$ $$\mathrm{For}\:{f}\left({x},{y}\right)\:\leqslant\mathrm{0},\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{chose}\:{a}\:\mathrm{such} \\ $$ $$\mathrm{that}\:\mathrm{value}\:\mathrm{at}\:\mathrm{maxima}\:\mathrm{is}\:\mathrm{0}. \\ $$ $${f}_{{x}} ={ae}^{{x}} +{e}^{{x}} \mathrm{sin}\:{x}+{e}^{{x}} \mathrm{cos}\:{x} \\ $$ $${f}_{{y}} =−\left({ae}^{{y}} +{e}^{{x}} \mathrm{sin}\:{y}+{e}^{{x}} \mathrm{cos}\:{y}\right) \\ $$ $${function}\:{f}\:{will}\:{attain}\:{maxima}\:{or}\:{minima} \\ $$ $${when}\:{f}_{{x}} \:{and}\:{f}_{{y}} \:{are}\:{both}\:\mathrm{0}. \\ $$ $${f}_{{x}} =\mathrm{0}\Rightarrow{e}^{{x}} \left({a}+\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)=\mathrm{0} \\ $$ $${a}+\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{0} \\ $$ $$\mathrm{similarly} \\ $$ $${a}+\sqrt{\mathrm{2}}\mathrm{sin}\:\left({y}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{0} \\ $$ $$\mathrm{The}\:\mathrm{critical}\:\mathrm{points}\:\mathrm{are}\:\mathrm{given}\:\mathrm{by}: \\ $$ $${x}=\mathrm{2}\pi{n}+\mathrm{2tan}^{−\mathrm{1}} \left(\frac{−\sqrt{\mathrm{2}−{a}^{\mathrm{2}} }−\mathrm{1}}{{a}−\mathrm{1}}\right),\:{n}\in\mathbb{Z} \\ $$ $${y}=\mathrm{2}\pi{m}+\mathrm{2tan}^{−\mathrm{1}} \left(\frac{−\sqrt{\mathrm{2}−{a}^{\mathrm{2}} }−\mathrm{1}}{{a}−\mathrm{1}}\right),\:{m}\in\mathbb{Z} \\ $$ $$\mathrm{The}\:\mathrm{problem}\:\mathrm{statement}\:\mathrm{is}\:\mathrm{to}\:\mathrm{chose}\:{a}\:\mathrm{such} \\ $$ $$\mathrm{that}\:{f}\left({x},{y}\right)\leqslant\mathrm{0}\:\mathrm{at}\:\mathrm{critical}\:\mathrm{points}. \\ $$ $$\mathrm{To}\:\mathrm{be}\:\mathrm{continued}\:\mathrm{in}\:\mathrm{answer}. \\ $$

Answered by prakash jain last updated on 20/Nov/15

At critical point of f(x,y) sinx=siny so the given inequality is satisfied by all a>1 (∵e^(y−x) ≥1) I am not 100% confident of the answer since I expected a value different than 1. comments? The answer a=1 is wrong (see comments below). Wrong conclusion was arrived as critical points for f(x,y) in the comments are only for LOCAL MAXIMA.

$$\mathrm{At}\:\mathrm{critical}\:\mathrm{point}\:\mathrm{of}\:{f}\left({x},{y}\right)\:\mathrm{sin}{x}=\mathrm{sin}{y} \\ $$ $$\mathrm{so}\:\mathrm{the}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{satisfied}\:\mathrm{by}\:\mathrm{all} \\ $$ $${a}>\mathrm{1}\:\left(\because{e}^{{y}−{x}} \geqslant\mathrm{1}\right) \\ $$ $$\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{100\%}\:\mathrm{confident}\:\mathrm{of}\:\mathrm{the}\:\mathrm{answer} \\ $$ $$\mathrm{since}\:\mathrm{I}\:\mathrm{expected}\:\mathrm{a}\:\mathrm{value}\:\mathrm{different}\:\mathrm{than}\:\mathrm{1}. \\ $$ $$\mathrm{comments}? \\ $$ $$\mathrm{The}\:\mathrm{answer}\:{a}=\mathrm{1}\:\mathrm{is}\:\mathrm{wrong}\:\left(\mathrm{see}\:\mathrm{comments}\right. \\ $$ $$\left.\mathrm{below}\right).\: \\ $$ $$\mathrm{Wrong}\:\mathrm{conclusion}\:\mathrm{was}\:\mathrm{arrived}\:\mathrm{as}\:\mathrm{critical} \\ $$ $$\mathrm{points}\:\mathrm{for}\:{f}\left({x},{y}\right)\:\mathrm{in}\:\mathrm{the}\:\mathrm{comments}\:\mathrm{are}\:\mathrm{only} \\ $$ $$\mathrm{for}\:\mathrm{LOCAL}\:\mathrm{MAXIMA}.\: \\ $$

Commented byYozzi last updated on 20/Nov/15

I′m unsure about how to tackle the problem, but how about this. If x=y the inequality becomes ((a+sinx)/(a+sinx))≤e^0 . ∵ a>1 ⇒∄x,a∈R∣a+sinx=0. So 1≤1 and hence the inequality holds. In this case there isn′t any smallest a∈R since one can infinitely set a to be a value above 1 and very close to 1. No highest lower bound exists for the set {a∈R∣a>1}. For y>x⇒y−x>0⇒e^(y−x) >e^0 =1 ∴1−e^(y−x) <0. Keeping note of this we have ((a+sinx)/(a+siny))≤e^(y−x) [a+sinx,a+siny>0 ∵ a>1] a+sinx≤ae^(y−x) +e^(y−x) siny a(1−e^(y−x) )≤e^(y−x) siny−sinx ⇒a≥((e^(y−x) siny−sinx)/(1−e^(y−x) )) [1−e^(y−x) <0] a≥((e^(y−x) siny)/(1−e^(y−x) ))−((sinx)/(1−e^(y−x) )) (∗) If the RHS of the inequality above is strictly greater than 1 then the smallest a possible would be found to be a=((e^(y−x) siny−sinx)/(1−e^(y−x) )). If this is true then ((e^(y−x) siny−sinx)/(1−e^(y−x) ))>1 e^(y−x) siny−sinx<1−e^(y−x) e^(y−x) (siny+1)<1+sinx If siny+1≠0 (otherwise siny+1>0) ∴e^(y−x) <((1+sinx)/(1+siny)) Checking that this is obeyed by the proposed value for a ((((e^(y−x) siny−sinx)/(1−e^(y−x) ))+sinx)/(((e^(y−x) siny−sinx)/(1−e^(y−x) ))+siny))≤e^(y−x) ((e^(y−x) siny−sinx+sinx−e^(y−x) )/(e^(y−x) siny−sinx+siny−e^(y−x) siny))≤e^(y−x) ((e^(y−x) (siny−1))/(siny−sinx))≤e^(y−x) ((siny−1)/(siny−sinx))≤1. y>x so siny≠sinx. If siny>sinx siny−1≤siny−sinx⇒sinx≤1 (possible) If siny<sinx⇒siny−1≥siny−sinx sinx≥1 (possible if x=nπ+(−1)^n (π/2)) Together the cases suggest that the inequality holds for all x<y, if siny+1≠0. If the RHS of (∗) is not greater than 1 I don′t know how one could acquire the necessary value for a from the information given. In this case we must have a>1.

$${I}'{m}\:{unsure}\:{about}\:{how}\:{to}\:{tackle} \\ $$ $${the}\:{problem},\:{but}\:{how}\:{about} \\ $$ $${this}.\: \\ $$ $${If}\:{x}={y}\:{the}\:{inequality}\:{becomes} \\ $$ $$\frac{{a}+{sinx}}{{a}+{sinx}}\leqslant{e}^{\mathrm{0}} .\:\because\:{a}>\mathrm{1}\:\Rightarrow\nexists{x},{a}\in\mathbb{R}\mid{a}+{sinx}=\mathrm{0}. \\ $$ $${So}\:\:\mathrm{1}\leqslant\mathrm{1}\:{and}\:{hence}\:{the}\:{inequality} \\ $$ $${holds}.\:{In}\:{this}\:{case} \\ $$ $${there}\:{isn}'{t}\:{any}\:{smallest}\:{a}\in\mathbb{R}\:{since} \\ $$ $${one}\:{can}\:{infinitely}\:{set}\:{a}\:{to}\:{be}\:{a}\:{value}\:{above}\:\mathrm{1} \\ $$ $${and}\:{very}\:{close}\:{to}\:\mathrm{1}.\:{No}\:{highest}\:{lower}\:{bound} \\ $$ $${exists}\:{for}\:{the}\:{set}\:\left\{{a}\in\mathbb{R}\mid{a}>\mathrm{1}\right\}. \\ $$ $$ \\ $$ $${For}\:{y}>{x}\Rightarrow{y}−{x}>\mathrm{0}\Rightarrow{e}^{{y}−{x}} >{e}^{\mathrm{0}} =\mathrm{1} \\ $$ $$\therefore\mathrm{1}−{e}^{{y}−{x}} <\mathrm{0}.\:{Keeping}\:{note}\:{of}\:{this}\:{we} \\ $$ $${have}\: \\ $$ $$\frac{{a}+{sinx}}{{a}+{siny}}\leqslant{e}^{{y}−{x}} \:\:\:\:\:\:\:\left[{a}+{sinx},{a}+{siny}>\mathrm{0}\:\because\:{a}>\mathrm{1}\right] \\ $$ $${a}+{sinx}\leqslant{ae}^{{y}−{x}} +{e}^{{y}−{x}} {siny} \\ $$ $${a}\left(\mathrm{1}−{e}^{{y}−{x}} \right)\leqslant{e}^{{y}−{x}} {siny}−{sinx} \\ $$ $$\Rightarrow{a}\geqslant\frac{{e}^{{y}−{x}} {siny}−{sinx}}{\mathrm{1}−{e}^{{y}−{x}} }\:\:\:\:\:\:\:\left[\mathrm{1}−{e}^{{y}−{x}} <\mathrm{0}\right] \\ $$ $${a}\geqslant\frac{{e}^{{y}−{x}} {siny}}{\mathrm{1}−{e}^{{y}−{x}} }−\frac{{sinx}}{\mathrm{1}−{e}^{{y}−{x}} }\:\:\:\left(\ast\right) \\ $$ $$ \\ $$ $${If}\:{the}\:{RHS}\:{of}\:{the}\:{inequality}\:{above} \\ $$ $${is}\:{strictly}\:{greater}\:{than}\:\mathrm{1}\:{then}\:{the}\: \\ $$ $${smallest}\:{a}\:{possible}\:{would}\:{be}\:{found}\:{to} \\ $$ $${be}\:{a}=\frac{{e}^{{y}−{x}} {siny}−{sinx}}{\mathrm{1}−{e}^{{y}−{x}} }. \\ $$ $${If}\:{this}\:{is}\:{true}\:{then} \\ $$ $$\frac{{e}^{{y}−{x}} {siny}−{sinx}}{\mathrm{1}−{e}^{{y}−{x}} }>\mathrm{1} \\ $$ $${e}^{{y}−{x}} {siny}−{sinx}<\mathrm{1}−{e}^{{y}−{x}} \\ $$ $${e}^{{y}−{x}} \left({siny}+\mathrm{1}\right)<\mathrm{1}+{sinx} \\ $$ $${If}\:{siny}+\mathrm{1}\neq\mathrm{0}\:\:\left({otherwise}\:{siny}+\mathrm{1}>\mathrm{0}\right) \\ $$ $$\therefore{e}^{{y}−{x}} <\frac{\mathrm{1}+{sinx}}{\mathrm{1}+{siny}} \\ $$ $$ \\ $$ $${Checking}\:{that}\:{this}\:{is}\:{obeyed}\:{by}\:{the} \\ $$ $${proposed}\:{value}\:{for}\:{a}\: \\ $$ $$\frac{\frac{{e}^{{y}−{x}} {siny}−{sinx}}{\mathrm{1}−{e}^{{y}−{x}} }+{sinx}}{\frac{{e}^{{y}−{x}} {siny}−{sinx}}{\mathrm{1}−{e}^{{y}−{x}} }+{siny}}\leqslant{e}^{{y}−{x}} \\ $$ $$\frac{{e}^{{y}−{x}} {siny}−{sinx}+{sinx}−{e}^{{y}−{x}} }{{e}^{{y}−{x}} {siny}−{sinx}+{siny}−{e}^{{y}−{x}} {siny}}\leqslant{e}^{{y}−{x}} \\ $$ $$\frac{{e}^{{y}−{x}} \left({siny}−\mathrm{1}\right)}{{siny}−{sinx}}\leqslant{e}^{{y}−{x}} \\ $$ $$\frac{{siny}−\mathrm{1}}{{siny}−{sinx}}\leqslant\mathrm{1}. \\ $$ $${y}>{x}\:{so}\:{siny}\neq{sinx}.\:{If}\:{siny}>{sinx} \\ $$ $${siny}−\mathrm{1}\leqslant{siny}−{sinx}\Rightarrow{sinx}\leqslant\mathrm{1}\:\left({possible}\right) \\ $$ $$ \\ $$ $${If}\:{siny}<{sinx}\Rightarrow{siny}−\mathrm{1}\geqslant{siny}−{sinx} \\ $$ $${sinx}\geqslant\mathrm{1}\:\left({possible}\:{if}\:{x}={n}\pi+\left(−\mathrm{1}\right)^{{n}} \left(\pi/\mathrm{2}\right)\right) \\ $$ $$ \\ $$ $${Together}\:{the}\:{cases}\:{suggest}\:{that}\:{the}\:{inequality}\:{holds} \\ $$ $${for}\:{all}\:{x}<{y},\:{if}\:{siny}+\mathrm{1}\neq\mathrm{0}. \\ $$ $$ \\ $$ $${If}\:{the}\:{RHS}\:{of}\:\left(\ast\right)\:{is}\:{not}\:{greater}\:{than}\:\mathrm{1}\:{I} \\ $$ $${don}'{t}\:{know}\:{how}\:{one}\:{could}\:{acquire} \\ $$ $${the}\:{necessary}\:{value}\:{for}\:{a}\:{from}\:{the} \\ $$ $${information}\:{given}.\:{In}\:{this}\:{case}\:{we} \\ $$ $${must}\:{have}\: \\ $$ $${a}>\mathrm{1}.\: \\ $$ $$ \\ $$

Commented byYozzi last updated on 20/Nov/15

This question is from an admissions quiz and I think its purpose is to see how one breaks it down rather than obtaining just a value for a. It′s all about the process rather than the answer.

$${This}\:{question}\:{is}\:{from}\:{an}\:{admissions} \\ $$ $${quiz}\:{and}\:{I}\:{think}\:{its}\:{purpose}\:{is}\:{to}\:{see} \\ $$ $${how}\:{one}\:{breaks}\:{it}\:{down}\:{rather}\:{than} \\ $$ $${obtaining}\:{just}\:{a}\:{value}\:{for}\:{a}.\:{It}'{s}\: \\ $$ $${all}\:{about}\:{the}\:{process}\:{rather}\:{than}\:{the} \\ $$ $${answer}. \\ $$

Commented byprakash jain last updated on 20/Nov/15

Ok. The answer a>1 is wrong ((1.01+sin x)/(1.01+sin y))≤e^(y−x) x=(π/2), y=((3π)/2) ((2.01)/(0.01))=201≰e^π

$$\mathrm{Ok}.\:\mathrm{The}\:\mathrm{answer}\:{a}>\mathrm{1}\:{is}\:{wrong} \\ $$ $$\frac{\mathrm{1}.\mathrm{01}+\mathrm{sin}\:{x}}{\mathrm{1}.\mathrm{01}+\mathrm{sin}\:{y}}\leqslant{e}^{{y}−{x}} \\ $$ $${x}=\frac{\pi}{\mathrm{2}},\:{y}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$ $$\frac{\mathrm{2}.\mathrm{01}}{\mathrm{0}.\mathrm{01}}=\mathrm{201}\nleq{e}^{\pi} \\ $$

Commented byYozzi last updated on 20/Nov/15

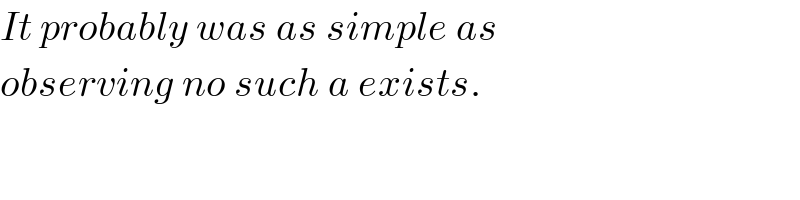
It probably was as simple as observing no such a exists.

$${It}\:{probably}\:{was}\:{as}\:{simple}\:{as}\: \\ $$ $${observing}\:{no}\:{such}\:{a}\:{exists}. \\ $$

Commented byprakash jain last updated on 20/Nov/15

I have updated answer on where the error is in the original arguments. If the answer is no such a exists then we need to prove that there is no global maxima for f(x,y) with y>x.

$$\mathrm{I}\:\mathrm{have}\:\mathrm{updated}\:\mathrm{answer}\:\mathrm{on}\:\mathrm{where}\:\mathrm{the}\:\mathrm{error}\:\mathrm{is} \\ $$ $$\mathrm{in}\:\mathrm{the}\:\mathrm{original}\:\mathrm{arguments}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{answer} \\ $$ $$\mathrm{is}\:\mathrm{no}\:\mathrm{such}\:{a}\:\mathrm{exists}\:\mathrm{then}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{prove} \\ $$ $$\mathrm{that}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{global}\:\mathrm{maxima}\:\mathrm{for}\:{f}\left({x},{y}\right) \\ $$ $$\mathrm{with}\:{y}>{x}. \\ $$

Commented byYozzi last updated on 20/Nov/15

Yes.

$${Yes}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com