Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 24540 by Tinkutara last updated on 20/Nov/17

Prove that (i) Σ_(n=0) ^∞ (n^2 /(n!))=2e. (ii) Σ_(n=0) ^∞ (n^3 /(n!))=5e. (iii) Σ_(n=0) ^∞ (n^4 /(n!))=15e.

$${Prove}\:{that} \\ $$$$\left({i}\right)\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} }{{n}!}=\mathrm{2}{e}. \\ $$$$\left({ii}\right)\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{3}} }{{n}!}=\mathrm{5}{e}. \\ $$$$\left({iii}\right)\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{4}} }{{n}!}=\mathrm{15}{e}. \\ $$

Commented by prakash jain last updated on 20/Nov/17

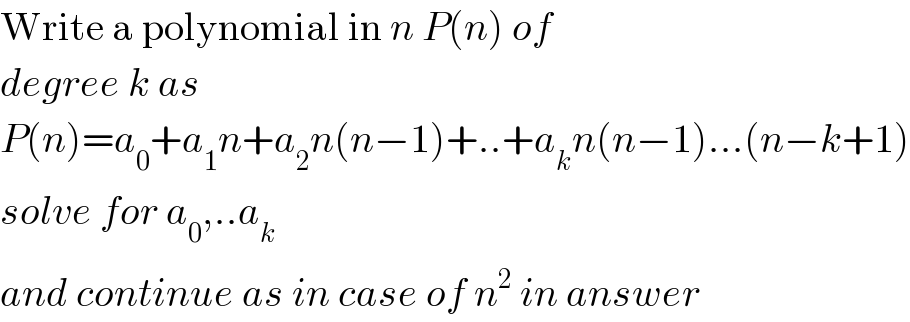
Write a polynomial in n P(n) of degree k as P(n)=a_0 +a_1 n+a_2 n(n−1)+..+a_k n(n−1)...(n−k+1) solve for a_0 ,..a_k and continue as in case of n^2 in answer

$$\mathrm{Write}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{in}\:{n}\:{P}\left({n}\right)\:{of} \\ $$$${degree}\:{k}\:{as} \\ $$$${P}\left({n}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {n}+{a}_{\mathrm{2}} {n}\left({n}−\mathrm{1}\right)+..+{a}_{{k}} {n}\left({n}−\mathrm{1}\right)...\left({n}−{k}+\mathrm{1}\right) \\ $$$${solve}\:{for}\:{a}_{\mathrm{0}} ,..{a}_{{k}} \\ $$$${and}\:{continue}\:{as}\:{in}\:{case}\:{of}\:{n}^{\mathrm{2}} \:{in}\:{answer} \\ $$

Answered by prakash jain last updated on 20/Nov/17

n^2 =n+n(n−1) Σ_(n=0) ^∞ ((n+n(n−1))/(n!)) =Σ_(n=1) ^∞ (1/((n−1)!))+Σ_(n=2) ^∞ (1/((n−2)!)) =e+e=2e

$${n}^{\mathrm{2}} ={n}+{n}\left({n}−\mathrm{1}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}+{n}\left({n}−\mathrm{1}\right)}{{n}!} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\mathrm{2}\right)!} \\ $$$$={e}+{e}=\mathrm{2}{e} \\ $$

Commented by Tinkutara last updated on 21/Nov/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by ajfour last updated on 20/Nov/17

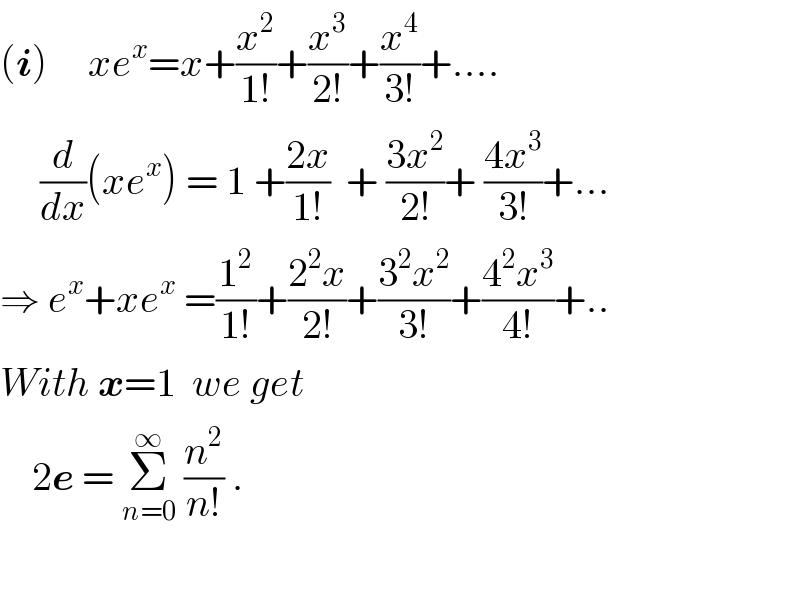
(i) xe^x =x+(x^2 /(1!))+(x^3 /(2!))+(x^4 /(3!))+.... (d/dx)(xe^x ) = 1 +((2x)/(1!)) + ((3x^2 )/(2!))+ ((4x^3 )/(3!))+... ⇒ e^x +xe^x =(1^2 /(1!))+((2^2 x)/(2!))+((3^2 x^2 )/(3!))+((4^2 x^3 )/(4!))+.. With x=1 we get 2e = Σ_(n=0) ^∞ (n^2 /(n!)) .

$$\left(\boldsymbol{{i}}\right)\:\:\:\:\:{xe}^{{x}} ={x}+\frac{{x}^{\mathrm{2}} }{\mathrm{1}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{3}!}+.... \\ $$$$\:\:\:\:\:\frac{{d}}{{dx}}\left({xe}^{{x}} \right)\:=\:\mathrm{1}\:+\frac{\mathrm{2}{x}}{\mathrm{1}!}\:\:+\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}!}+\:\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{3}!}+... \\ $$$$\Rightarrow\:{e}^{{x}} +{xe}^{{x}} \:=\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{1}!}+\frac{\mathrm{2}^{\mathrm{2}} {x}}{\mathrm{2}!}+\frac{\mathrm{3}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{\mathrm{4}^{\mathrm{2}} {x}^{\mathrm{3}} }{\mathrm{4}!}+.. \\ $$$${With}\:\boldsymbol{{x}}=\mathrm{1}\:\:{we}\:{get} \\ $$$$\:\:\:\:\mathrm{2}\boldsymbol{{e}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{n}^{\mathrm{2}} }{{n}!}\:. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 21/Nov/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com