Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 2466 by prakash jain last updated on 20/Nov/15

(√(−(1/5) ))−(1/(√(−5)))=?

$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}\:}−\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}}=? \\ $$

Answered by Yozzi last updated on 20/Nov/15

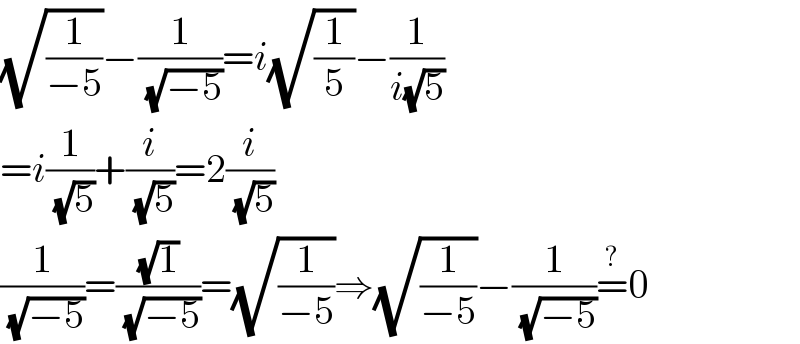
(√(1/(−5)))−(1/(√(−5)))=i(√(1/5))−(1/(i(√5))) =i(1/(√5))+(i/(√5))=2(i/(√5)) (1/(√(−5)))=((√1)/(√(−5)))=(√(1/(−5)))⇒(√(1/(−5)))−(1/(√(−5)))=^? 0

$$\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}−\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}}={i}\sqrt{\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\mathrm{1}}{{i}\sqrt{\mathrm{5}}} \\ $$$$={i}\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}+\frac{{i}}{\sqrt{\mathrm{5}}}=\mathrm{2}\frac{{i}}{\sqrt{\mathrm{5}}} \\ $$$$\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}}=\frac{\sqrt{\mathrm{1}}}{\sqrt{−\mathrm{5}}}=\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}\Rightarrow\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}−\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}}\overset{?} {=}\mathrm{0} \\ $$

Commented by prakash jain last updated on 20/Nov/15

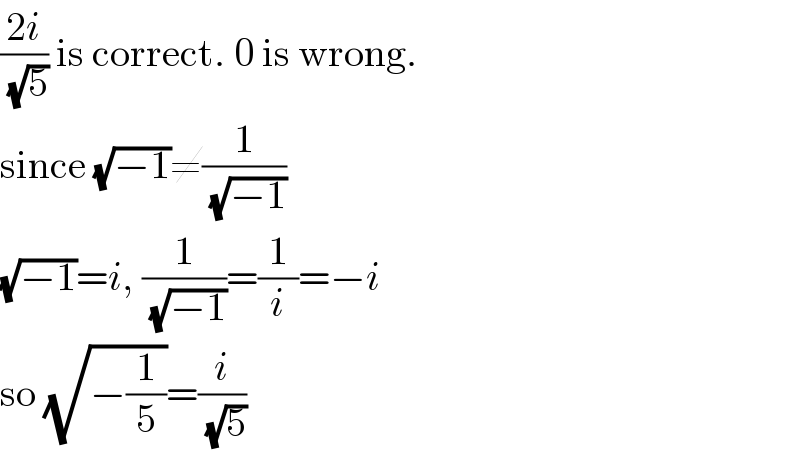
((2i)/(√5)) is correct. 0 is wrong. since (√(−1))≠(1/(√(−1))) (√(−1))=i, (1/(√(−1)))=(1/i)=−i so (√(−(1/5)))=(i/(√5))

$$\frac{\mathrm{2}{i}}{\sqrt{\mathrm{5}}}\:\mathrm{is}\:\mathrm{correct}.\:\mathrm{0}\:\mathrm{is}\:\mathrm{wrong}. \\ $$$$\mathrm{since}\:\sqrt{−\mathrm{1}}\neq\frac{\mathrm{1}}{\sqrt{−\mathrm{1}}} \\ $$$$\sqrt{−\mathrm{1}}={i},\:\frac{\mathrm{1}}{\sqrt{−\mathrm{1}}}=\frac{\mathrm{1}}{{i}}=−{i} \\ $$$$\mathrm{so}\:\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}=\frac{{i}}{\sqrt{\mathrm{5}}} \\ $$

Commented by Yozzi last updated on 20/Nov/15

I see.

$${I}\:{see}.\: \\ $$

Answered by Rasheed Soomro last updated on 21/Nov/15

(√(−(1/5) ))−(1/(√(−5)))=? (√(−(1/5)))−((√1)/(√(−5))) (√(−(1/5)))−(√(1/(−5))) ∵ ((√a)/(√b))=(√(a/b)) (√(−(1/5)))−(√(−(1/5))) ∵ ((+ve)/(−ve))=−ve =0 ∵a−a=0 Where is logical mistake?

$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}\:}−\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}}=? \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\sqrt{\mathrm{1}}}{\sqrt{−\mathrm{5}}} \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\sqrt{\frac{\mathrm{1}}{−\mathrm{5}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\because\:\frac{\sqrt{{a}}}{\sqrt{{b}}}=\sqrt{\frac{{a}}{{b}}} \\ $$$$\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\because\:\frac{+{ve}}{−{ve}}=−{ve} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because{a}−{a}=\mathrm{0} \\ $$$${Where}\:{is}\:{logical}\:{mistake}? \\ $$

Commented by Filup last updated on 21/Nov/15

It has to do with the laws of complex radicals. e.g. 1≠(√((−1)(−1)))=(√(−1))(√(−1))=i^2 =−1 Which is incorrect (√a)×(√b)≠(√(−a))×(√(−b)) (√a)×(√(−b))≠(√(−a))×(√b) (in some situations) such as: for: (√(−(1/5)))−(1/(√(−5)))⇒(√(−(1/5)))≠(1/(√(−5)))

$$\mathrm{It}\:\mathrm{has}\:\mathrm{to}\:\mathrm{do}\:\mathrm{with}\:\mathrm{the}\:\mathrm{laws}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{radicals}. \\ $$$$ \\ $$$$\mathrm{e}.\mathrm{g}. \\ $$$$\mathrm{1}\neq\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}=\sqrt{−\mathrm{1}}\sqrt{−\mathrm{1}}={i}^{\mathrm{2}} =−\mathrm{1} \\ $$$${Which}\:{is}\:{incorrect} \\ $$$$ \\ $$$$\sqrt{{a}}×\sqrt{{b}}\neq\sqrt{−{a}}×\sqrt{−{b}} \\ $$$$\sqrt{{a}}×\sqrt{−{b}}\neq\sqrt{−{a}}×\sqrt{{b}}\:\:\:\:\left(\mathrm{in}\:\mathrm{some}\:\mathrm{situations}\right) \\ $$$$ \\ $$$${such}\:{as}: \\ $$$$\mathrm{for}:\:\:\:\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}−\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}}\Rightarrow\sqrt{−\frac{\mathrm{1}}{\mathrm{5}}}\neq\frac{\mathrm{1}}{\sqrt{−\mathrm{5}}} \\ $$

Commented by Rasheed Soomro last updated on 21/Nov/15

THanKs. That means (√(ab))=(√a)(√b) and (√(a/b))=((√a)/(√b)) are restricted. They are aplicable only when a>0 and b>0.

$$\mathcal{T}\mathfrak{HanKs}. \\ $$$${That}\:{means}\:\sqrt{{ab}}=\sqrt{{a}}\sqrt{{b}}\:\:{and}\:\sqrt{\frac{{a}}{{b}}}=\frac{\sqrt{{a}}}{\sqrt{{b}}}\:\:\:{are}\:{restricted}. \\ $$$${They}\:{are}\:{aplicable}\:{only}\:{when}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0}. \\ $$

Commented by Filup last updated on 21/Nov/15

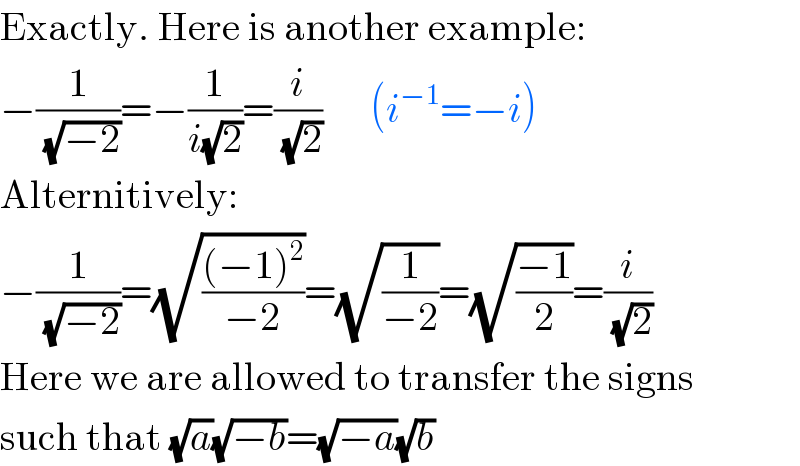
Exactly. Here is another example: −(1/(√(−2)))=−(1/(i(√2)))=(i/(√2)) (i^(−1) =−i) Alternitively: −(1/(√(−2)))=(√(((−1)^2 )/(−2)))=(√(1/(−2)))=(√((−1)/2))=(i/(√2)) Here we are allowed to transfer the signs such that (√a)(√(−b))=(√(−a))(√b)

$$\mathrm{Exactly}.\:\mathrm{Here}\:\mathrm{is}\:\mathrm{another}\:\mathrm{example}: \\ $$$$−\frac{\mathrm{1}}{\sqrt{−\mathrm{2}}}=−\frac{\mathrm{1}}{{i}\sqrt{\mathrm{2}}}=\frac{{i}}{\sqrt{\mathrm{2}}}\:\:\:\:\:\:\left({i}^{−\mathrm{1}} =−{i}\right) \\ $$$$\mathrm{Alternitively}: \\ $$$$−\frac{\mathrm{1}}{\sqrt{−\mathrm{2}}}=\sqrt{\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} }{−\mathrm{2}}}=\sqrt{\frac{\mathrm{1}}{−\mathrm{2}}}=\sqrt{\frac{−\mathrm{1}}{\mathrm{2}}}=\frac{{i}}{\sqrt{\mathrm{2}}} \\ $$$$\mathrm{Here}\:\mathrm{we}\:\mathrm{are}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{transfer}\:\mathrm{the}\:\mathrm{signs} \\ $$$$\mathrm{such}\:\mathrm{that}\:\sqrt{{a}}\sqrt{−{b}}=\sqrt{−{a}}\sqrt{{b}} \\ $$

Commented by Filup last updated on 21/Nov/15

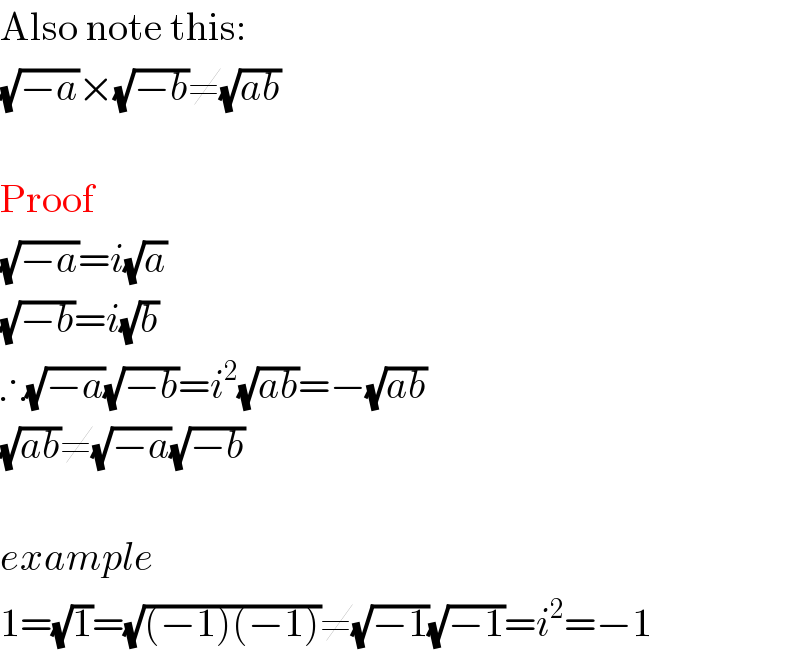
Also note this: (√(−a))×(√(−b))≠(√(ab)) Proof (√(−a))=i(√a) (√(−b))=i(√b) ∴(√(−a))(√(−b))=i^2 (√(ab))=−(√(ab)) (√(ab))≠(√(−a))(√(−b)) example 1=(√1)=(√((−1)(−1)))≠(√(−1))(√(−1))=i^2 =−1

$$\mathrm{Also}\:\mathrm{note}\:\mathrm{this}: \\ $$$$\sqrt{−{a}}×\sqrt{−{b}}\neq\sqrt{{ab}} \\ $$$$ \\ $$$$\mathrm{Proof} \\ $$$$\sqrt{−{a}}={i}\sqrt{{a}} \\ $$$$\sqrt{−{b}}={i}\sqrt{{b}} \\ $$$$\therefore\sqrt{−{a}}\sqrt{−{b}}={i}^{\mathrm{2}} \sqrt{{ab}}=−\sqrt{{ab}} \\ $$$$\sqrt{{ab}}\neq\sqrt{−{a}}\sqrt{−{b}} \\ $$$$ \\ $$$${example} \\ $$$$\mathrm{1}=\sqrt{\mathrm{1}}=\sqrt{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}\neq\sqrt{−\mathrm{1}}\sqrt{−\mathrm{1}}={i}^{\mathrm{2}} =−\mathrm{1} \\ $$

Commented by Rasheed Soomro last updated on 22/Nov/15

Is (√(−a))(√b) =(√(−ab ))? [ a,b>0]

$${Is}\:\sqrt{−{a}}\sqrt{{b}}\:=\sqrt{−{ab}\:}?\:\:\:\:\:\:\:\:\:\left[\:{a},{b}>\mathrm{0}\right] \\ $$

Answered by Filup last updated on 21/Nov/15

Follwing the laws of complex radicles, both answers of ((2i)/(√5)) and 0 are correct. I belive that we have two solutions. ((2i)/(√5)) is our complex solution (ℑ(z)=(2/(√5))) 0 is our real solution If z=ℜ(z)+ℑ(z) we have: z=0+((2i)/(√5))

$$\mathrm{Follwing}\:\mathrm{the}\:\mathrm{laws}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{radicles}, \\ $$$$\mathrm{both}\:\mathrm{answers}\:\mathrm{of}\:\:\frac{\mathrm{2}{i}}{\sqrt{\mathrm{5}}}\:\:\mathrm{and}\:\mathrm{0}\:{are}\:{correct}. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{belive}\:\mathrm{that}\:\mathrm{we}\:\mathrm{have}\:\mathrm{two}\:\mathrm{solutions}. \\ $$$$\frac{\mathrm{2}{i}}{\sqrt{\mathrm{5}}}\:\mathrm{is}\:\mathrm{our}\:\mathrm{complex}\:\mathrm{solution}\:\:\left(\Im\left({z}\right)=\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\right) \\ $$$$\mathrm{0}\:\mathrm{is}\:\mathrm{our}\:\mathrm{real}\:\mathrm{solution} \\ $$$$ \\ $$$$\mathrm{If}\:\:{z}=\Re\left({z}\right)+\Im\left({z}\right)\:\:\mathrm{we}\:\mathrm{have}: \\ $$$${z}=\mathrm{0}+\frac{\mathrm{2}{i}}{\sqrt{\mathrm{5}}} \\ $$

Commented by Rasheed Soomro last updated on 22/Nov/15

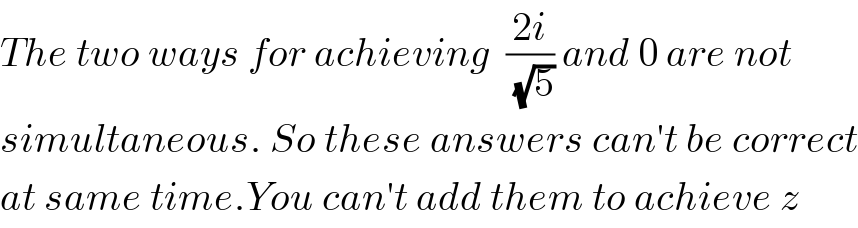
The two ways for achieving ((2i)/(√5)) and 0 are not simultaneous. So these answers can′t be correct at same time.You can′t add them to achieve z

$${The}\:{two}\:{ways}\:{for}\:{achieving}\:\:\frac{\mathrm{2}{i}}{\sqrt{\mathrm{5}}}\:{and}\:\mathrm{0}\:{are}\:{not} \\ $$$${simultaneous}.\:{So}\:{these}\:{answers}\:{can}'{t}\:{be}\:{correct} \\ $$$${at}\:{same}\:{time}.{You}\:{can}'{t}\:{add}\:{them}\:{to}\:{achieve}\:{z} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com