Question Number 24739 by Tinkutara last updated on 25/Nov/17

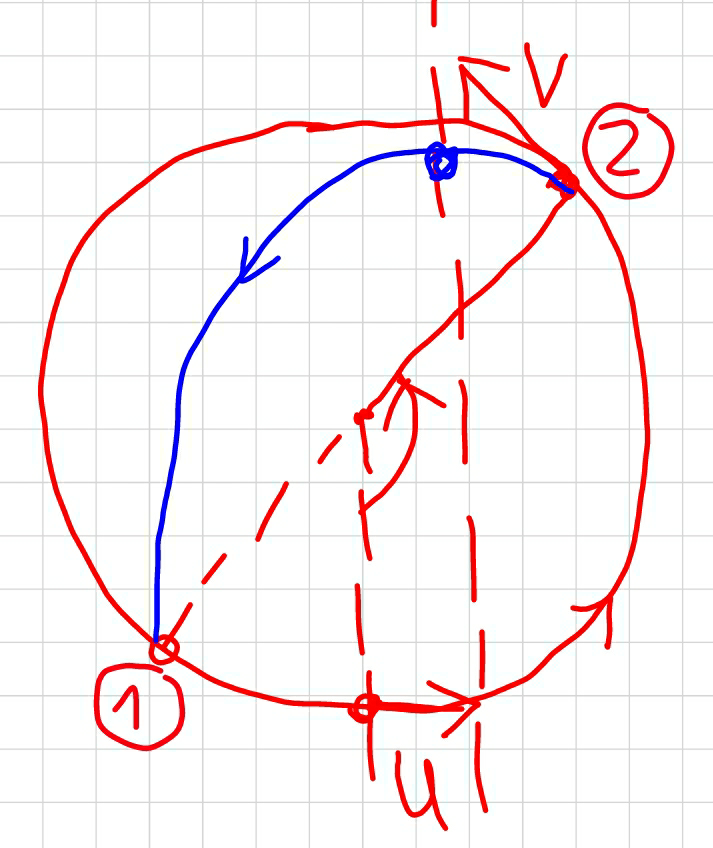
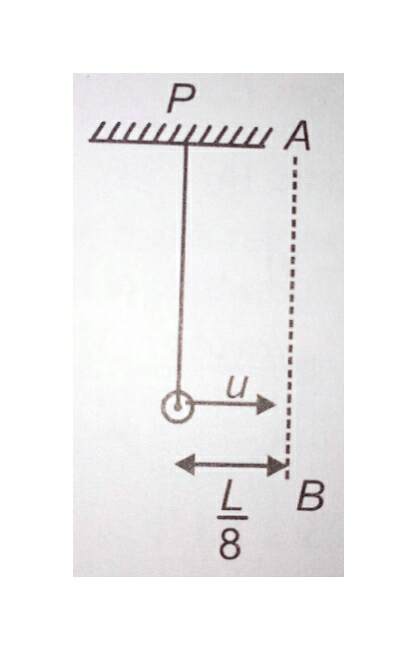
$${A}\:{particle}\:{is}\:{suspended}\:{vertically} \\ $$$${from}\:{point}\:{O}\:{by}\:{ideal}\:{string}\:{of}\:{length} \\ $$$${L}.\:{It}\:{is}\:{given}\:{horizontal}\:{velocity}\:'{v}'. \\ $$$${There}\:{is}\:{vertical}\:{line}\:{AB}\:{at}\:{a}\:{distance} \\ $$$$\frac{{L}}{\mathrm{8}}\:{from}\:{P}.\:{At}\:{some}\:{point},\:{it}\:{leaves} \\ $$$${circular}\:{motion}\:{and}\:{follows}\:{projectile} \\ $$$${motion}.\:{At}\:{the}\:{instant}\:{it}\:{crosses}\:{AB}, \\ $$$${its}\:{velocity}\:{is}\:{horizontal}.\:{Find}\:{u} \\ $$
Commented by Tinkutara last updated on 25/Nov/17
Commented by ajfour last updated on 25/Nov/17
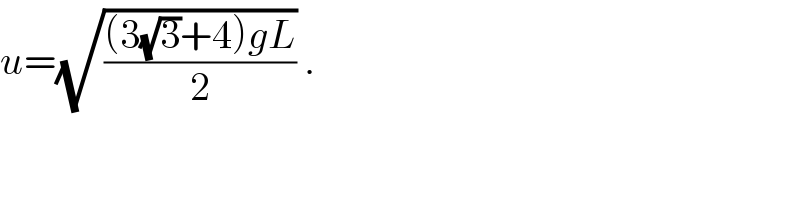
$${u}=\sqrt{\frac{\left(\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{4}\right){gL}}{\mathrm{2}}}\:. \\ $$
Commented by Tinkutara last updated on 25/Nov/17

$${How}? \\ $$
Commented by ajfour last updated on 25/Nov/17
Commented by ajfour last updated on 25/Nov/17
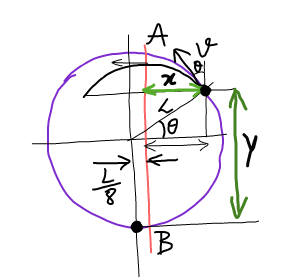
![(1/2)m(u^2 −v^2 )=mgy=mgL(1+sin θ) ....(i) ((mv^2 )/L)=mgsin θ ⇒ v^2 =gLsin θ ..(ii) x=(R/2)=((v^2 sin [2(90−θ)])/(2g))=Lcos θ−(L/8) ⇒gLsin θ×((2sin θcos θ)/(2g))=L(cos θ−(1/8)) ⇒ cos θ(1−cos^2 θ)=cos θ−(1/8) or cos θ=(1/2) Now from (i): v^2 =(((√3)gL)/2) using this in (i): u^2 =v^2 +2gL(1+sin θ) =(((√3)gL)/2)+2gL(1+((√3)/2)) or u= (√(((3(√3)+4)gL)/2)) .](Q24757.png)
$$\frac{\mathrm{1}}{\mathrm{2}}{m}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right)={mgy}={mgL}\left(\mathrm{1}+\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({i}\right) \\ $$$$\frac{{mv}^{\mathrm{2}} }{{L}}={mg}\mathrm{sin}\:\theta\:\:\Rightarrow\:{v}^{\mathrm{2}} ={gL}\mathrm{sin}\:\theta\:\:..\left({ii}\right) \\ $$$${x}=\frac{{R}}{\mathrm{2}}=\frac{{v}^{\mathrm{2}} \mathrm{sin}\:\left[\mathrm{2}\left(\mathrm{90}−\theta\right)\right]}{\mathrm{2}{g}}={L}\mathrm{cos}\:\theta−\frac{{L}}{\mathrm{8}} \\ $$$$\Rightarrow{gL}\mathrm{sin}\:\theta×\frac{\mathrm{2sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}{g}}={L}\left(\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{8}}\right) \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)=\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${or}\:\:\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${Now}\:{from}\:\left({i}\right):\:\:\:{v}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}{gL}}{\mathrm{2}} \\ $$$${using}\:{this}\:{in}\:\left({i}\right): \\ $$$${u}^{\mathrm{2}} ={v}^{\mathrm{2}} +\mathrm{2}{gL}\left(\mathrm{1}+\mathrm{sin}\:\theta\right) \\ $$$$\:\:\:\:=\frac{\sqrt{\mathrm{3}}{gL}}{\mathrm{2}}+\mathrm{2}{gL}\left(\mathrm{1}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${or}\:\:\:\boldsymbol{{u}}=\:\sqrt{\frac{\left(\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{4}\right)\boldsymbol{{gL}}}{\mathrm{2}}}\:. \\ $$
Commented by Tinkutara last updated on 25/Nov/17
![x=(R/2)=((v^2 sin [2(90−θ)])/(2g))=Lcos θ−(L/8) How this L(cos θ−(1/8))?](Q24768.png)
$${x}=\frac{{R}}{\mathrm{2}}=\frac{{v}^{\mathrm{2}} \mathrm{sin}\:\left[\mathrm{2}\left(\mathrm{90}−\theta\right)\right]}{\mathrm{2}{g}}={L}\mathrm{cos}\:\theta−\frac{{L}}{\mathrm{8}} \\ $$$${How}\:{this}\:{L}\left(\mathrm{cos}\:\theta−\frac{\mathrm{1}}{\mathrm{8}}\right)? \\ $$
Commented by ajfour last updated on 25/Nov/17

$${see}\:{diagram},\:{x}={L}\mathrm{cos}\:\theta−\frac{{L}}{\mathrm{8}} \\ $$$${since}\:{velocity}\:{is}\:{horizontal} \\ $$$${when}\:{as}\:{a}\:{projectile}\:{mass}\:'{m}' \\ $$$${crosses}\:{AB}\:{so}\:{from}\:{the}\:{point} \\ $$$${where}\:{circular}\:{motion}\:{ends} \\ $$$${and}\:{till}\:{line}\:{AB}\:{is}\:{reached}\:{the} \\ $$$${horizontal}\:{distance}\: \\ $$$$\boldsymbol{{x}}={v}_{{x}} \bigtriangleup{t}=\left({v}\mathrm{sin}\:\theta\right)\left(\frac{{v}\mathrm{cos}\:\theta}{{g}}\right). \\ $$
Commented by Tinkutara last updated on 26/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 27/Nov/17
$$\theta,\:{for}\:{a}\:{reason}\:{is}\:{acute}\:{angled}.. \\ $$
Commented by ajfour last updated on 28/Nov/17
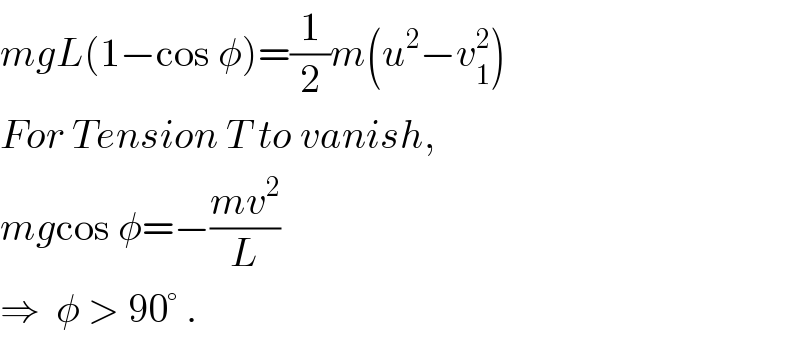
$${mgL}\left(\mathrm{1}−\mathrm{cos}\:\phi\right)=\frac{\mathrm{1}}{\mathrm{2}}{m}\left({u}^{\mathrm{2}} −{v}_{\mathrm{1}} ^{\mathrm{2}} \right) \\ $$$${For}\:{Tension}\:{T}\:{to}\:{vanish}, \\ $$$${mg}\mathrm{cos}\:\phi=−\frac{{mv}^{\mathrm{2}} }{{L}} \\ $$$$\Rightarrow\:\:\phi\:>\:\mathrm{90}°\:. \\ $$
Commented by mrW1 last updated on 28/Nov/17

$${Thank}\:{you}\:{sir}! \\ $$$${Now}\:{I}\:{understand}\:{the}\:{question}\:{totally}. \\ $$$${Can}\:{you}\:{find}\:{the}\:{point}\:{where}\:{the} \\ $$$${particle}\:{comes}\:{back}? \\ $$
Commented by mrW1 last updated on 28/Nov/17