Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2481 by Syaka last updated on 21/Nov/15

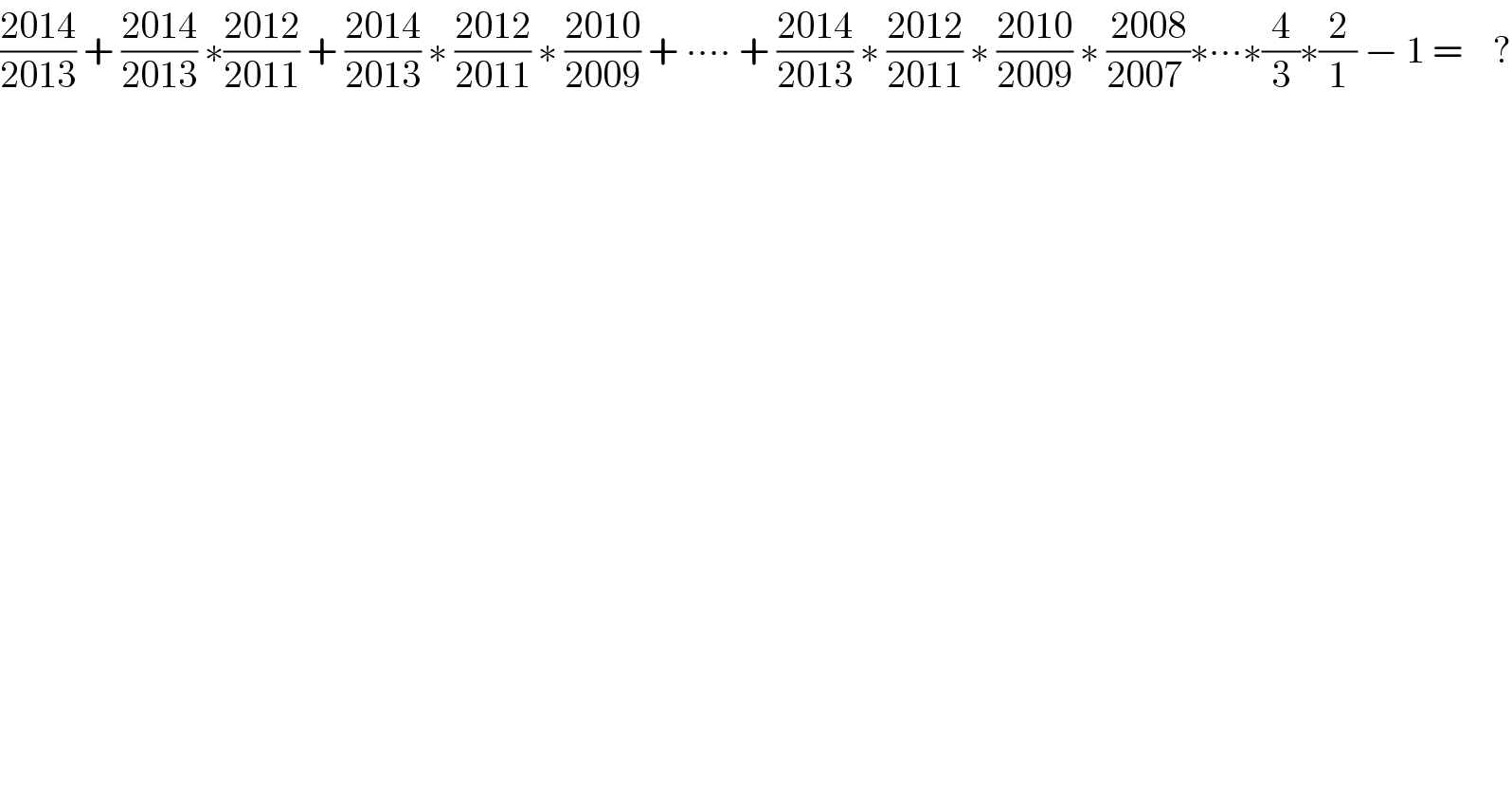
((2014)/(2013)) + ((2014)/(2013)) ∗((2012)/(2011)) + ((2014)/(2013)) ∗ ((2012)/(2011)) ∗ ((2010)/(2009)) + ∙∙∙∙ + ((2014)/(2013)) ∗ ((2012)/(2011)) ∗ ((2010)/(2009)) ∗ ((2008)/(2007 ))∗∙∙∙∗(4/3)∗(2/1) − 1 = ?

$$\frac{\mathrm{2014}}{\mathrm{2013}}\:+\:\frac{\mathrm{2014}}{\mathrm{2013}}\:\ast\frac{\mathrm{2012}}{\mathrm{2011}}\:+\:\frac{\mathrm{2014}}{\mathrm{2013}}\:\ast\:\frac{\mathrm{2012}}{\mathrm{2011}}\:\ast\:\frac{\mathrm{2010}}{\mathrm{2009}}\:+\:\centerdot\centerdot\centerdot\centerdot\:+\:\frac{\mathrm{2014}}{\mathrm{2013}}\:\ast\:\frac{\mathrm{2012}}{\mathrm{2011}}\:\ast\:\frac{\mathrm{2010}}{\mathrm{2009}}\:\ast\:\frac{\mathrm{2008}}{\mathrm{2007}\:}\ast\centerdot\centerdot\centerdot\ast\frac{\mathrm{4}}{\mathrm{3}}\ast\frac{\mathrm{2}}{\mathrm{1}}\:−\:\mathrm{1}\:=\:\:\:\:? \\ $$

Answered by Filup last updated on 21/Nov/15

if by ′′∗′′ you mean ′′×′′ in form (k=2014): S=((k/(k−1))+((k(k−2))/((k−1)(k−3)))+((k(k−2)(k−4))/(k(k−1)(k−3)(k−5)))+...)−1 According to WolframAlpha: Sum=(Σ_(n=1) ^m (k/((1+k−2n))))−1 where m=((2014)/(2013))×...(4/3)×(2/1) m=Π_(l=1) ^k ((l+1)/l)=k+1=2015 (W.Alpha) ∴S=Σ_(n=1) ^(2015) (((2014)/(2015−2n)))−1 continue not sure how to evaluate this, if at all correct

$$\mathrm{if}\:\mathrm{by}\:''\ast''\:\mathrm{you}\:\mathrm{mean}\:''×'' \\ $$$${in}\:{form}\:\left({k}=\mathrm{2014}\right): \\ $$$$ \\ $$$${S}=\left(\frac{{k}}{{k}−\mathrm{1}}+\frac{{k}\left({k}−\mathrm{2}\right)}{\left({k}−\mathrm{1}\right)\left({k}−\mathrm{3}\right)}+\frac{{k}\left({k}−\mathrm{2}\right)\left({k}−\mathrm{4}\right)}{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{3}\right)\left({k}−\mathrm{5}\right)}+...\right)−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{WolframAlpha}: \\ $$$${Sum}=\left(\underset{{n}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{k}}{\left(\mathrm{1}+{k}−\mathrm{2}{n}\right)}\right)−\mathrm{1} \\ $$$$\mathrm{where}\:{m}=\frac{\mathrm{2014}}{\mathrm{2013}}×...\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{2}}{\mathrm{1}} \\ $$$${m}=\underset{{l}=\mathrm{1}} {\overset{{k}} {\prod}}\frac{{l}+\mathrm{1}}{{l}}={k}+\mathrm{1}=\mathrm{2015}\:\:\:\:\:\:\:\left({W}.{Alpha}\right) \\ $$$$ \\ $$$$\therefore{S}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\left(\frac{\mathrm{2014}}{\mathrm{2015}−\mathrm{2}{n}}\right)−\mathrm{1} \\ $$$$ \\ $$$${continue} \\ $$$$\mathrm{not}\:\mathrm{sure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{evaluate}\:\mathrm{this},\:\mathrm{if}\:\mathrm{at}\:\mathrm{all} \\ $$$$\mathrm{correct} \\ $$

Answered by prakash jain last updated on 24/Nov/15

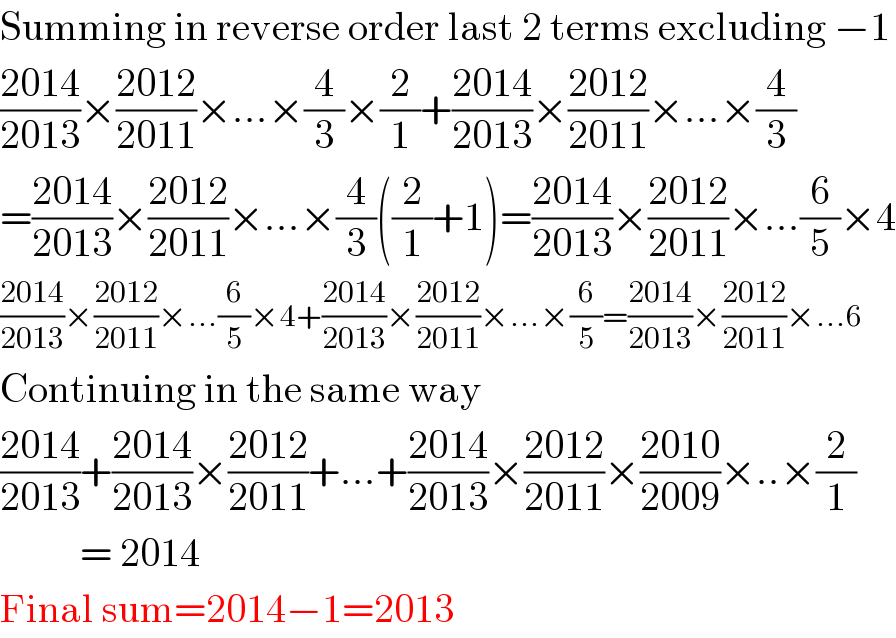
Summing in reverse order last 2 terms excluding −1 ((2014)/(2013))×((2012)/(2011))×...×(4/3)×(2/1)+((2014)/(2013))×((2012)/(2011))×...×(4/3) =((2014)/(2013))×((2012)/(2011))×...×(4/3)((2/1)+1)=((2014)/(2013))×((2012)/(2011))×...(6/5)×4 ((2014)/(2013))×((2012)/(2011))×...(6/5)×4+((2014)/(2013))×((2012)/(2011))×...×(6/5)=((2014)/(2013))×((2012)/(2011))×...6 Continuing in the same way ((2014)/(2013))+((2014)/(2013))×((2012)/(2011))+...+((2014)/(2013))×((2012)/(2011))×((2010)/(2009))×..×(2/1) = 2014 Final sum=2014−1=2013

$$\mathrm{Summing}\:\mathrm{in}\:\mathrm{reverse}\:\mathrm{order}\:\mathrm{last}\:\mathrm{2}\:\mathrm{terms}\:\mathrm{excluding}\:−\mathrm{1} \\ $$$$\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...×\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{2}}{\mathrm{1}}+\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...×\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...×\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{1}}+\mathrm{1}\right)=\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...\frac{\mathrm{6}}{\mathrm{5}}×\mathrm{4} \\ $$$$\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...\frac{\mathrm{6}}{\mathrm{5}}×\mathrm{4}+\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...×\frac{\mathrm{6}}{\mathrm{5}}=\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×...\mathrm{6} \\ $$$$\mathrm{Continuing}\:\mathrm{in}\:\mathrm{the}\:\mathrm{same}\:\mathrm{way} \\ $$$$\frac{\mathrm{2014}}{\mathrm{2013}}+\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}+...+\frac{\mathrm{2014}}{\mathrm{2013}}×\frac{\mathrm{2012}}{\mathrm{2011}}×\frac{\mathrm{2010}}{\mathrm{2009}}×..×\frac{\mathrm{2}}{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2014} \\ $$$$\mathrm{Final}\:\mathrm{sum}=\mathrm{2014}−\mathrm{1}=\mathrm{2013} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com