
Question and Answers Forum
Question Number 24831 by Eng.Firas last updated on 27/Nov/17
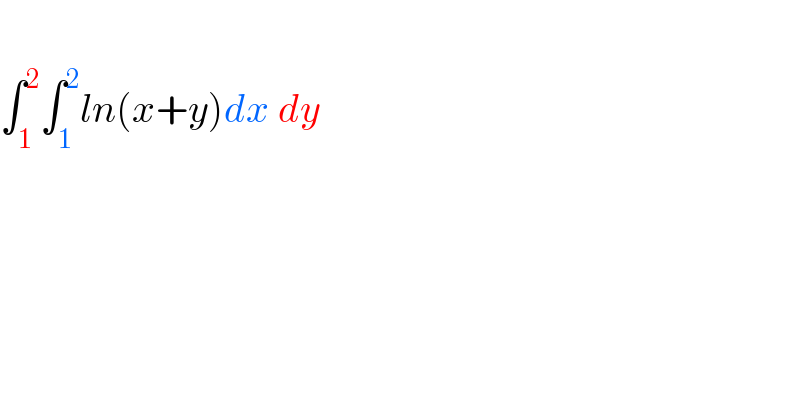
Answered by prakash jain last updated on 27/Nov/17
![∫_1 ^2 ∫_1 ^2 ln(x+y)dxdy =∫_1 ^2 [(x+y)ln (x+y)−x]_1 ^2 dy =∫_1 ^2 {(2+y)ln (y+2)−2−(1+y)ln (1+y)+1}dy =∫_1 ^2 {(2+y)ln (y+2)−(1+y)ln (1+y)−1}dy ∫_1 ^2 (2+y)ln (y+2)dy =[ln (y+2)(((2+y)^2 )/2)−(((2+y)^2 )/4)]_1 ^2 =[(ln 4)(4^2 /2)−(4^2 /4)−(ln 3)(3^2 /2)+(3^2 /4)] =8ln 4−8−(9/2)ln 3+(9/4) ∫_1 ^2 (1+y)ln (y+1)dy =[ln (y+1)(((1+y)^2 )/2)−(((1+y)^2 )/4)]_1 ^2 =(9/2)ln 3−(9/4)−(2^2 /2)ln 2+(2^2 /4) ∫_1 ^2 (−1)dy=−1 ans=8ln 4−8−2ln 2+1−1 =16ln 2−8−2ln 2 =14ln 2−8](Q24850.png)
Commented by Eng.Firas last updated on 27/Nov/17

| ||
Question and Answers Forum | ||
Question Number 24831 by Eng.Firas last updated on 27/Nov/17 | ||
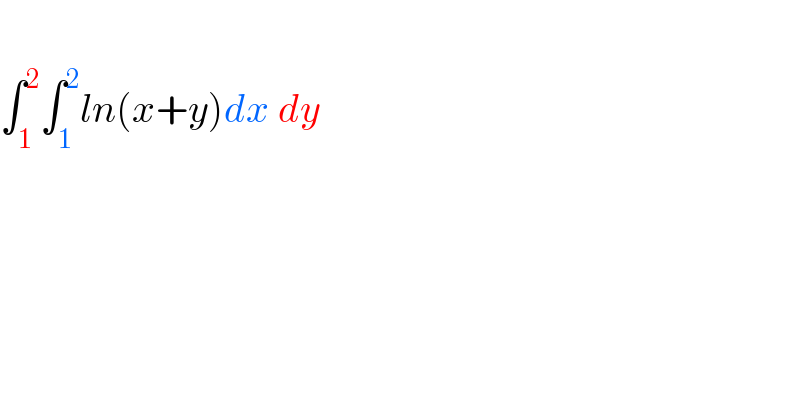 | ||
Answered by prakash jain last updated on 27/Nov/17 | ||
![∫_1 ^2 ∫_1 ^2 ln(x+y)dxdy =∫_1 ^2 [(x+y)ln (x+y)−x]_1 ^2 dy =∫_1 ^2 {(2+y)ln (y+2)−2−(1+y)ln (1+y)+1}dy =∫_1 ^2 {(2+y)ln (y+2)−(1+y)ln (1+y)−1}dy ∫_1 ^2 (2+y)ln (y+2)dy =[ln (y+2)(((2+y)^2 )/2)−(((2+y)^2 )/4)]_1 ^2 =[(ln 4)(4^2 /2)−(4^2 /4)−(ln 3)(3^2 /2)+(3^2 /4)] =8ln 4−8−(9/2)ln 3+(9/4) ∫_1 ^2 (1+y)ln (y+1)dy =[ln (y+1)(((1+y)^2 )/2)−(((1+y)^2 )/4)]_1 ^2 =(9/2)ln 3−(9/4)−(2^2 /2)ln 2+(2^2 /4) ∫_1 ^2 (−1)dy=−1 ans=8ln 4−8−2ln 2+1−1 =16ln 2−8−2ln 2 =14ln 2−8](Q24850.png) | ||
| ||
Commented by Eng.Firas last updated on 27/Nov/17 | ||
 | ||