Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 25001 by Tinkutara last updated on 30/Nov/17

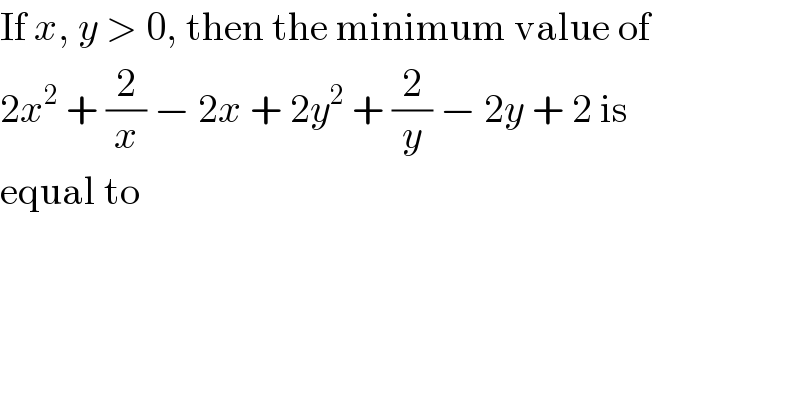
If x, y > 0, then the minimum value of 2x^2 + (2/x) − 2x + 2y^2 + (2/y) − 2y + 2 is equal to

$$\mathrm{If}\:{x},\:{y}\:>\:\mathrm{0},\:\mathrm{then}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$ $$\mathrm{2}{x}^{\mathrm{2}} \:+\:\frac{\mathrm{2}}{{x}}\:−\:\mathrm{2}{x}\:+\:\mathrm{2}{y}^{\mathrm{2}} \:+\:\frac{\mathrm{2}}{{y}}\:−\:\mathrm{2}{y}\:+\:\mathrm{2}\:\mathrm{is} \\ $$ $$\mathrm{equal}\:\mathrm{to} \\ $$

Commented byprakash jain last updated on 01/Dec/17

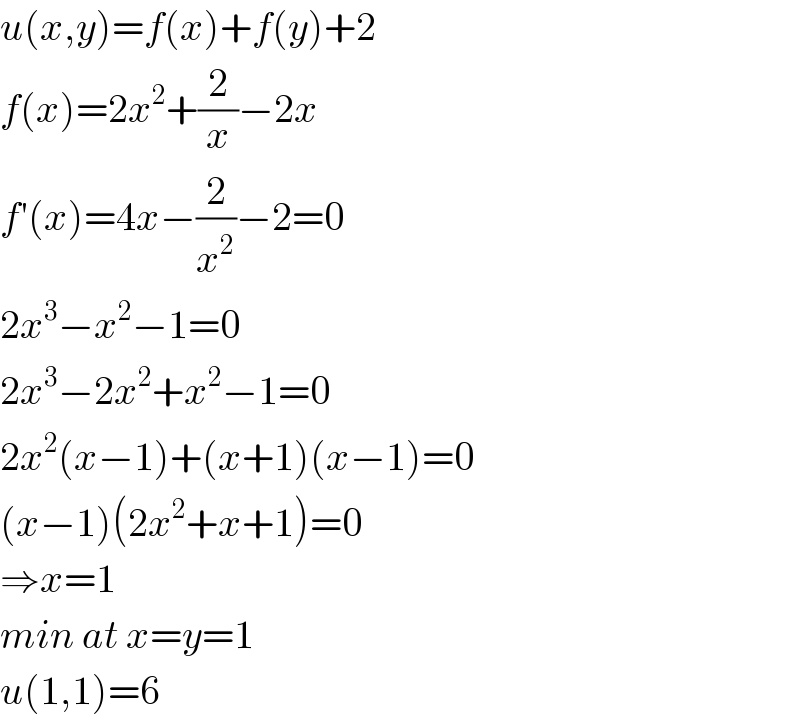
u(x,y)=f(x)+f(y)+2 f(x)=2x^2 +(2/x)−2x f′(x)=4x−(2/x^2 )−2=0 2x^3 −x^2 −1=0 2x^3 −2x^2 +x^2 −1=0 2x^2 (x−1)+(x+1)(x−1)=0 (x−1)(2x^2 +x+1)=0 ⇒x=1 min at x=y=1 u(1,1)=6

$${u}\left({x},{y}\right)={f}\left({x}\right)+{f}\left({y}\right)+\mathrm{2} \\ $$ $${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} +\frac{\mathrm{2}}{{x}}−\mathrm{2}{x} \\ $$ $${f}'\left({x}\right)=\mathrm{4}{x}−\frac{\mathrm{2}}{{x}^{\mathrm{2}} }−\mathrm{2}=\mathrm{0} \\ $$ $$\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$ $$\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$ $$\mathrm{2}{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)+\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$ $$\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$ $$\Rightarrow{x}=\mathrm{1} \\ $$ $${min}\:{at}\:{x}={y}=\mathrm{1} \\ $$ $${u}\left(\mathrm{1},\mathrm{1}\right)=\mathrm{6} \\ $$

Commented byTinkutara last updated on 01/Dec/17

Thank you Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$

Commented byTinkutara last updated on 01/Dec/17

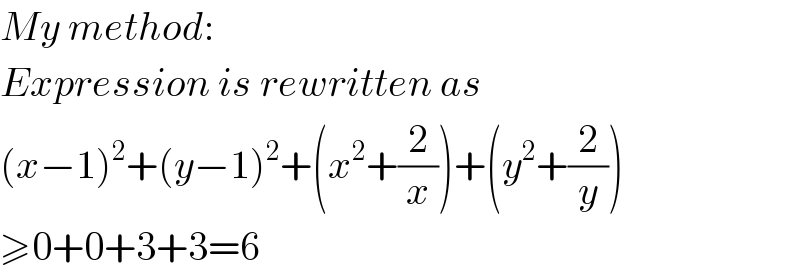
My method: Expression is rewritten as (x−1)^2 +(y−1)^2 +(x^2 +(2/x))+(y^2 +(2/y)) ≥0+0+3+3=6

$${My}\:{method}: \\ $$ $${Expression}\:{is}\:{rewritten}\:{as} \\ $$ $$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\frac{\mathrm{2}}{{x}}\right)+\left({y}^{\mathrm{2}} +\frac{\mathrm{2}}{{y}}\right) \\ $$ $$\geqslant\mathrm{0}+\mathrm{0}+\mathrm{3}+\mathrm{3}=\mathrm{6} \\ $$

Commented byprakash jain last updated on 01/Dec/17

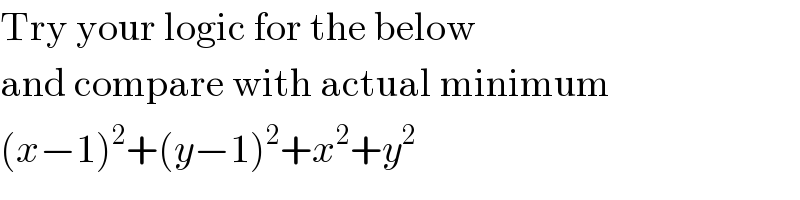
Try your logic for the below and compare with actual minimum (x−1)^2 +(y−1)^2 +x^2 +y^2

$$\mathrm{Try}\:\mathrm{your}\:\mathrm{logic}\:\mathrm{for}\:\mathrm{the}\:\mathrm{below} \\ $$ $$\mathrm{and}\:\mathrm{compare}\:\mathrm{with}\:\mathrm{actual}\:\mathrm{minimum} \\ $$ $$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$

Commented byprakash jain last updated on 01/Dec/17

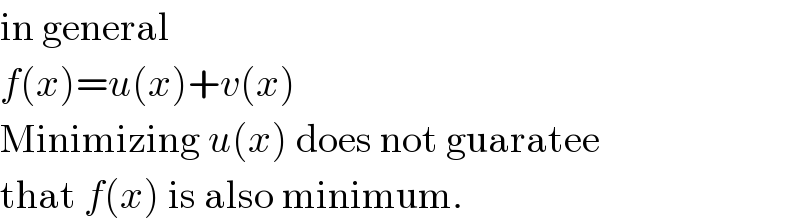
in general f(x)=u(x)+v(x) Minimizing u(x) does not guaratee that f(x) is also minimum.

$$\mathrm{in}\:\mathrm{general} \\ $$ $${f}\left({x}\right)={u}\left({x}\right)+{v}\left({x}\right) \\ $$ $$\mathrm{Minimizing}\:{u}\left({x}\right)\:\mathrm{does}\:\mathrm{not}\:\mathrm{guaratee} \\ $$ $$\mathrm{that}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{also}\:\mathrm{minimum}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com