
Question Number 25049 by Tinkutara last updated on 02/Dec/17
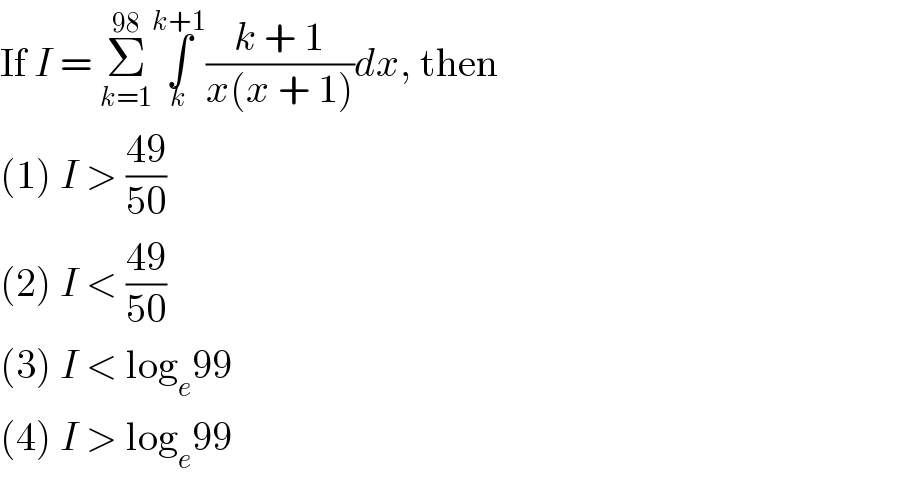
$$\mathrm{If}\:{I}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{98}} {\sum}}\underset{{k}} {\overset{{k}+\mathrm{1}} {\int}}\frac{{k}\:+\:\mathrm{1}}{{x}\left({x}\:+\:\mathrm{1}\right)}{dx},\:\mathrm{then} \\ $$ $$\left(\mathrm{1}\right)\:{I}\:>\:\frac{\mathrm{49}}{\mathrm{50}} \\ $$ $$\left(\mathrm{2}\right)\:{I}\:<\:\frac{\mathrm{49}}{\mathrm{50}} \\ $$ $$\left(\mathrm{3}\right)\:{I}\:<\:\mathrm{log}_{{e}} \mathrm{99} \\ $$ $$\left(\mathrm{4}\right)\:{I}\:>\:\mathrm{log}_{{e}} \mathrm{99} \\ $$
Commented byajfour last updated on 02/Dec/17

$$\left(\mathrm{1}\right),\:\left(\mathrm{3}\right)\:. \\ $$
Answered by ajfour last updated on 08/Dec/17
![Let J_k =∫_k ^( k+1 ) ((k+1)/(x(x+1)))dx J_k =(k+1)∫_k ^( k+1 ) ((1/x)−(1/(x+1)))dx =(k+1)ln ((x/(x+1)))∣_k ^(k+1) =(k+1)ln [(((k+1)^2 )/(k(k+2)))] =2(k+1)[ln (k+1)−ln k−ln (k+2)] =[2(k+1)ln (k+1)−kln k −(k+2)ln (k+2)]+[−ln k+ln (k+2)] I=Σ_(k=1) ^(98) J_k =2Σ_(k=2) ^(99) kln k−Σ_(k=1) ^(98) kln k −Σ_(k=3) ^(100) kln k−Σ_(k=1) ^(98) ln k+Σ_(k=3) ^(100) ln k terms from k=3 to k=98 entirely cancel out, so I=4ln 2+2×99ln 99−2ln 2 −99ln 99−100ln 100−ln 2 +ln 99+ln 100 I =ln 2+99ln (((99)/(100)))+ln 99 = ln 99+99ln (1−(1/(100)))+ln 2 ≈ ln 99−0.99+0.3 So ((49)/(50)) < I < log _e 99 .](Q25063.png)
$${Let}\:\:\:\:{J}_{{k}} =\int_{{k}} ^{\:\:{k}+\mathrm{1}\:} \frac{{k}+\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)}{dx} \\ $$ $${J}_{{k}} =\left({k}+\mathrm{1}\right)\int_{{k}} ^{\:\:{k}+\mathrm{1}\:} \left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx} \\ $$ $$ \\ $$ $$\:\:\:\:\:=\left({k}+\mathrm{1}\right)\mathrm{ln}\:\left(\frac{{x}}{{x}+\mathrm{1}}\right)\mid_{{k}} ^{{k}+\mathrm{1}} \\ $$ $$\:\:\:\:\:=\left({k}+\mathrm{1}\right)\mathrm{ln}\:\left[\frac{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }{{k}\left({k}+\mathrm{2}\right)}\right] \\ $$ $$\:=\mathrm{2}\left({k}+\mathrm{1}\right)\left[\mathrm{ln}\:\left({k}+\mathrm{1}\right)−\mathrm{ln}\:{k}−\mathrm{ln}\:\left({k}+\mathrm{2}\right)\right] \\ $$ $$=\left[\mathrm{2}\left({k}+\mathrm{1}\right)\mathrm{ln}\:\left({k}+\mathrm{1}\right)−{k}\mathrm{ln}\:{k}\right. \\ $$ $$\left.\:\:\:−\left({k}+\mathrm{2}\right)\mathrm{ln}\:\left({k}+\mathrm{2}\right)\right]+\left[−\mathrm{ln}\:{k}+\mathrm{ln}\:\left({k}+\mathrm{2}\right)\right] \\ $$ $${I}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{98}} {\sum}}{J}_{{k}} =\mathrm{2}\underset{{k}=\mathrm{2}} {\overset{\mathrm{99}} {\sum}}{k}\mathrm{ln}\:{k}−\underset{{k}=\mathrm{1}} {\overset{\mathrm{98}} {\sum}}{k}\mathrm{ln}\:{k} \\ $$ $$\:\:\:\:\:\:\:\:\:−\underset{{k}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}{k}\mathrm{ln}\:{k}−\underset{{k}=\mathrm{1}} {\overset{\mathrm{98}} {\sum}}\mathrm{ln}\:{k}+\underset{{k}=\mathrm{3}} {\overset{\mathrm{100}} {\sum}}\mathrm{ln}\:{k} \\ $$ $${terms}\:{from}\:{k}=\mathrm{3}\:{to}\:{k}=\mathrm{98} \\ $$ $${entirely}\:{cancel}\:{out},\:{so} \\ $$ $$\:\:{I}=\mathrm{4ln}\:\mathrm{2}+\mathrm{2}×\mathrm{99ln}\:\mathrm{99}−\mathrm{2ln}\:\mathrm{2} \\ $$ $$\:\:−\mathrm{99ln}\:\mathrm{99}−\mathrm{100ln}\:\mathrm{100}−\mathrm{ln}\:\mathrm{2} \\ $$ $$\:\:\:\:+\mathrm{ln}\:\mathrm{99}+\mathrm{ln}\:\mathrm{100} \\ $$ $$\:\:{I}\:=\mathrm{ln}\:\mathrm{2}+\mathrm{99ln}\:\left(\frac{\mathrm{99}}{\mathrm{100}}\right)+\mathrm{ln}\:\mathrm{99} \\ $$ $$\:\:\:\:\:=\:\mathrm{ln}\:\mathrm{99}+\mathrm{99ln}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{100}}\right)+\mathrm{ln}\:\mathrm{2} \\ $$ $$\:\:\:\:\:\:\:\:\approx\:\mathrm{ln}\:\mathrm{99}−\mathrm{0}.\mathrm{99}+\mathrm{0}.\mathrm{3}\: \\ $$ $${So}\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{49}}{\mathrm{50}}\:<\:{I}\:<\:\mathrm{log}\:_{{e}} \mathrm{99}\:. \\ $$
Commented byTinkutara last updated on 03/Dec/17
$${I}\:{appreciate}\:{this}\:{Sir}. \\ $$
