
Question Number 25091 by Tinkutara last updated on 03/Dec/17

$${A}\:{particle}\:{of}\:{mass}\:{m}\:{moving}\:{with} \\ $$$${speed}\:{u}\:{collides}\:{perfectly}\:{inelastically} \\ $$$${with}\:{a}\:{sphere}\:{of}\:{radius}\:{R}\:{and}\:{same} \\ $$$${mass},\:{at}\:{rest},\:{at}\:{an}\:{impact}\:{parameter} \\ $$$${d}.\:{Find} \\ $$$$\left({a}\right)\:{Angle}\:{between}\:{their}\:{final}\:{velocities} \\ $$$$\left({b}\right)\:{Magnitude}\:{of}\:{their}\:{final} \\ $$$${velocities} \\ $$
Answered by ajfour last updated on 03/Dec/17

Commented by ajfour last updated on 04/Dec/17
![conserving linear momentum mu=2mv+mωRsin θ and sin θ=d/R , so 2v+ωd=u ...(i) conserving angular momentum about ground point G: mu(R+d)=mvR+(2/5)mR^2 ω+ m(v+ωRsin θ)(R+d)+mω(Rcos θ)^2 ....(ii) and as (Rcos θ)^2 =(R+d)(R−d), also Rsin θ=d ⇒ u(R+d)=vR+(2/5)ωR^2 + (v+ωd)(R+d)+ω(R^2 −d^2 ) from (i): v+ωd=u−v , so vd=ω((7/5)R^2 −d^2 ) and from (i): 2v+𝛚d=u ⇒ 2ω((7/5)R^2 −d^2 )+ωd^2 =ud ω=((ud)/((((14)/5)R^2 +d^2 ))) ; v=((u((7/5)R^2 −d^2 ))/((((14)/5)R^2 +d^2 ))) tan φ=((ωRcos θ)/(v+ωd)) =(d(√(R^2 −d^2 ))/((vd/ω)+d^2 )) tan 𝛗=((5d(√(R^2 −d^2 )))/(7R^2 )) . V=((ωRcos θ)/(sin φ)) =ω[((√(R^2 −d^2 ))/(sin φ))] .](Q25097.png)
$${conserving}\:{linear}\:{momentum} \\ $$$${mu}=\mathrm{2}{mv}+{m}\omega{R}\mathrm{sin}\:\theta \\ $$$${and}\:\mathrm{sin}\:\theta={d}/{R}\:\:,\:{so} \\ $$$$\:\:\mathrm{2}{v}+\omega{d}={u}\:\:\:...\left({i}\right) \\ $$$${conserving}\:{angular}\:{momentum} \\ $$$${about}\:{ground}\:{point}\:{G}: \\ $$$${mu}\left({R}+{d}\right)={mvR}+\frac{\mathrm{2}}{\mathrm{5}}{mR}^{\mathrm{2}} \omega+ \\ $$$$\:\:\:{m}\left({v}+\omega{R}\mathrm{sin}\:\theta\right)\left({R}+{d}\right)+{m}\omega\left({R}\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\left({ii}\right) \\ $$$${and}\:\:{as}\:\:\left({R}\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\left({R}+{d}\right)\left({R}−{d}\right), \\ $$$${also}\:{R}\mathrm{sin}\:\theta={d} \\ $$$$\Rightarrow\:\:{u}\left({R}+{d}\right)={vR}+\frac{\mathrm{2}}{\mathrm{5}}\omega{R}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left({v}+\omega{d}\right)\left({R}+{d}\right)+\omega\left({R}^{\mathrm{2}} −{d}^{\mathrm{2}} \right) \\ $$$${from}\:\left({i}\right):\:\:\:\:{v}+\omega{d}={u}−{v}\:\:,\:{so} \\ $$$$\:\:\:{vd}=\omega\left(\frac{\mathrm{7}}{\mathrm{5}}{R}^{\mathrm{2}} −{d}^{\mathrm{2}} \right) \\ $$$${and}\:{from}\:\left({i}\right):\:\:\:\:\:\:\mathrm{2}\boldsymbol{{v}}+\boldsymbol{\omega{d}}=\boldsymbol{{u}} \\ $$$$\Rightarrow\:\:\:\mathrm{2}\omega\left(\frac{\mathrm{7}}{\mathrm{5}}{R}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)+\omega{d}^{\mathrm{2}} ={ud} \\ $$$$\:\:\omega=\frac{{ud}}{\left(\frac{\mathrm{14}}{\mathrm{5}}{R}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)}\:;\:\boldsymbol{{v}}=\frac{\boldsymbol{{u}}\left(\frac{\mathrm{7}}{\mathrm{5}}\boldsymbol{{R}}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)}{\left(\frac{\mathrm{14}}{\mathrm{5}}{R}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)} \\ $$$$\mathrm{tan}\:\phi=\frac{\omega{R}\mathrm{cos}\:\theta}{{v}+\omega{d}}\:=\frac{{d}\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }}{\left({vd}/\omega\right)+{d}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\mathrm{tan}\:\boldsymbol{\phi}=\frac{\mathrm{5}\boldsymbol{{d}}\sqrt{\boldsymbol{{R}}^{\mathrm{2}} −\boldsymbol{{d}}^{\mathrm{2}} }}{\mathrm{7}\boldsymbol{{R}}^{\mathrm{2}} }\:. \\ $$$${V}=\frac{\omega{R}\mathrm{cos}\:\theta}{\mathrm{sin}\:\phi}\:=\omega\left[\frac{\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }}{\mathrm{sin}\:\phi}\right]\:. \\ $$
Commented by ajfour last updated on 03/Dec/17

$$\angle\:{between}\:{their}\:{final}\:{velocities} \\ $$$${is}\:\:\boldsymbol{\phi}\:. \\ $$$${final}\:{velocity}\:{of}\:{sphere}\:\boldsymbol{{v}}. \\ $$$${Final}\:{velocity}\:{of}\:{particle}\:{is}\:\boldsymbol{{V}}. \\ $$
Commented by Tinkutara last updated on 05/Dec/17
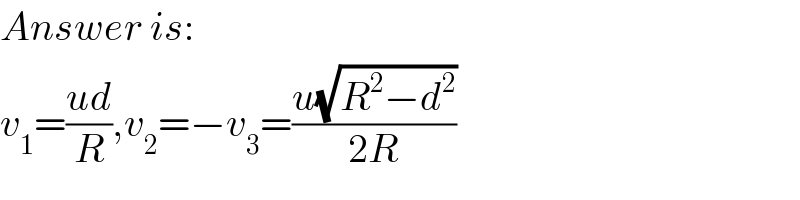
$${Answer}\:{is}: \\ $$$${v}_{\mathrm{1}} =\frac{{ud}}{{R}},{v}_{\mathrm{2}} =−{v}_{\mathrm{3}} =\frac{{u}\sqrt{{R}^{\mathrm{2}} −{d}^{\mathrm{2}} }}{\mathrm{2}{R}} \\ $$
Commented by ajfour last updated on 05/Dec/17

$${which}\:{answer}\:{is}\:{correct}\:{for} \\ $$$${d}=\mathrm{0}\:,\:{and}\:{even}\:{d}={R}\:?\:{Please} \\ $$$${check}\:{or}\:{i}\:{think}\:{i}\:{have}\: \\ $$$${misunderstood}\:{the}\:{question}. \\ $$$${mrW}\:{sir}\:{can}\:{help}\:{if}\:{he}\:{finds} \\ $$$${time}\:{and}\:{notices}\:{my}\:{request}. \\ $$
