Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 2526 by Filup last updated on 22/Nov/15

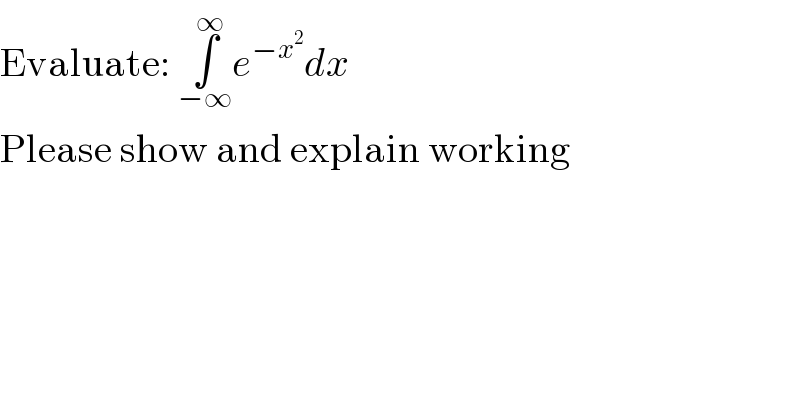
Evaluate: ∫_(−∞) ^∞ e^(−x^2 ) dx Please show and explain working

$$\mathrm{Evaluate}:\:\underset{−\infty} {\overset{\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$\mathrm{Please}\:\mathrm{show}\:\mathrm{and}\:\mathrm{explain}\:\mathrm{working} \\ $$

Commented by Filup last updated on 22/Nov/15

My current working: (unsure if correct) I=∫_(−∞) ^∞ e^(−x^2 ) dx=2∫_0 ^∞ e^(−x^2 ) dx ∴I=∫_0 ^∞ e^(−x^2 ) dx+∫_0 ^∞ e^(−y^2 ) dy I=∫_0 ^∞ ∫_0 ^∞ (e^(−x^2 ) +e^(−y^2 ) )dx dy

$$\mathrm{My}\:\mathrm{current}\:\mathrm{working}:\:\:\left(\mathrm{unsure}\:\mathrm{if}\:\mathrm{correct}\right) \\ $$$${I}=\underset{−\infty} {\overset{\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$\therefore{I}=\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx}+\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{y}^{\mathrm{2}} } {dy} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\infty} {\int}}\underset{\mathrm{0}} {\overset{\infty} {\int}}\left({e}^{−{x}^{\mathrm{2}} } +{e}^{−{y}^{\mathrm{2}} } \right){dx}\:{dy} \\ $$

Commented by 123456 last updated on 22/Nov/15

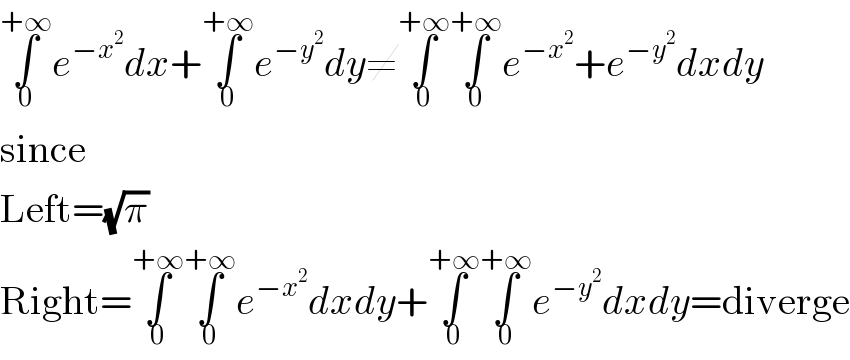
∫_0 ^(+∞) e^(−x^2 ) dx+∫_0 ^(+∞) e^(−y^2 ) dy≠∫_0 ^(+∞) ∫_0 ^(+∞) e^(−x^2 ) +e^(−y^2 ) dxdy since Left=(√π) Right=∫_0 ^(+∞) ∫_0 ^(+∞) e^(−x^2 ) dxdy+∫_0 ^(+∞) ∫_0 ^(+∞) e^(−y^2 ) dxdy=diverge

$$\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx}+\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−{y}^{\mathrm{2}} } {dy}\neq\underset{\mathrm{0}} {\overset{+\infty} {\int}}\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } +{e}^{−{y}^{\mathrm{2}} } {dxdy} \\ $$$$\mathrm{since} \\ $$$$\mathrm{Left}=\sqrt{\pi} \\ $$$$\mathrm{Right}=\underset{\mathrm{0}} {\overset{+\infty} {\int}}\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dxdy}+\underset{\mathrm{0}} {\overset{+\infty} {\int}}\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−{y}^{\mathrm{2}} } {dxdy}=\mathrm{diverge} \\ $$

Answered by 123456 last updated on 22/Nov/15

I=∫_(−∞) ^(+∞) e^(−x^2 ) dx>0 since e^(−x^2 ) ≥0∀x∈R I^2 =(∫_(−∞) ^(+∞) e^(−x^2 ) dx)^2 =∫_(−∞) ^(+∞) e^(−x^2 ) dx∫_(−∞) ^(+∞) e^(−y^2 ) dy squaring it I^2 =∫_(−∞) ^(+∞) ∫_(−∞) ^(+∞) e^(−x^2 −y^2 ) dxdy fubini theorem x=rcos θ y=rsin θ dxdy=rdrdθ jacobian determinant (((∂x/∂r),(∂x/∂θ)),((∂y/∂r),(∂y/∂θ)))= determinant (((cos θ),(−rsin θ)),((sin θ),(rcos θ)))=r 0≤x<+∞,0≤y<+∞ r=(√(x^2 +y^2 )) θ=arctan_2 (x,y) 0≤r<+∞,0≤θ<2π (new limits) I^2 =∫_0 ^(+∞) ∫_0 ^(2π) re^(−r^2 ) dθdr I^2 =∫_0 ^(+∞) re^(−r^2 ) dr∫_0 ^(2π) dθ=(1/2)∙2π=π ∫_0 ^(+∞) re^(−r^2 ) dr is solved at coment I=(√π) (>0)

$$\mathrm{I}=\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx}>\mathrm{0}\:\:\:\:\:\:\mathrm{since}\:{e}^{−{x}^{\mathrm{2}} } \geqslant\mathrm{0}\forall{x}\in\mathbb{R} \\ $$$$\mathrm{I}^{\mathrm{2}} =\left(\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} =\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} } {dx}\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−{y}^{\mathrm{2}} } {dy}\:\:\:\mathrm{squaring}\:\mathrm{it} \\ $$$$\mathrm{I}^{\mathrm{2}} =\underset{−\infty} {\overset{+\infty} {\int}}\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy}\:\:\:\:\:\mathrm{fubini}\:\mathrm{theorem} \\ $$$${x}={r}\mathrm{cos}\:\theta \\ $$$${y}={r}\mathrm{sin}\:\theta \\ $$$${dxdy}={rdrd}\theta\:\:\:\:\:\mathrm{jacobian}\:\begin{vmatrix}{\frac{\partial{x}}{\partial{r}}}&{\frac{\partial{x}}{\partial\theta}}\\{\frac{\partial{y}}{\partial{r}}}&{\frac{\partial{y}}{\partial\theta}}\end{vmatrix}=\begin{vmatrix}{\mathrm{cos}\:\theta}&{−{r}\mathrm{sin}\:\theta}\\{\mathrm{sin}\:\theta}&{{r}\mathrm{cos}\:\theta}\end{vmatrix}={r} \\ $$$$\mathrm{0}\leqslant{x}<+\infty,\mathrm{0}\leqslant{y}<+\infty \\ $$$${r}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\theta=\mathrm{arctan}_{\mathrm{2}} \left({x},{y}\right) \\ $$$$\mathrm{0}\leqslant{r}<+\infty,\mathrm{0}\leqslant\theta<\mathrm{2}\pi\:\:\:\:\left(\mathrm{new}\:\mathrm{limits}\right) \\ $$$$\mathrm{I}^{\mathrm{2}} =\underset{\mathrm{0}} {\overset{+\infty} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}{re}^{−{r}^{\mathrm{2}} } {d}\theta{dr} \\ $$$$\mathrm{I}^{\mathrm{2}} =\underset{\mathrm{0}} {\overset{+\infty} {\int}}{re}^{−{r}^{\mathrm{2}} } {dr}\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{2}\pi=\pi \\ $$$$\underset{\mathrm{0}} {\overset{+\infty} {\int}}{re}^{−{r}^{\mathrm{2}} } {dr}\:\mathrm{is}\:\mathrm{solved}\:\mathrm{at}\:\mathrm{coment} \\ $$$$\mathrm{I}=\sqrt{\pi}\:\:\left(>\mathrm{0}\right) \\ $$

Commented by Filup last updated on 22/Nov/15

Wow! ThankYou very much!

$${Wow}!\:\mathscr{T}{hank}\mathscr{Y}{ou}\:{very}\:{much}! \\ $$

Commented by Filup last updated on 22/Nov/15

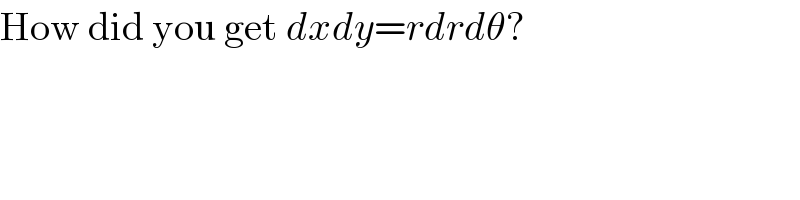
How did you get dxdy=rdrdθ?

$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:{dxdy}={rdrd}\theta? \\ $$

Commented by 123456 last updated on 22/Nov/15

jacobian of transformation J(r,θ)=((∂(r,θ))/(∂(x,y)))= determinant (((∂x/∂r),(∂x/∂θ)),((∂y/∂r),(∂y/∂θ))) dxdy=∣J(r,θ)∣drdθ

$$\mathrm{jacobian}\:\mathrm{of}\:\mathrm{transformation} \\ $$$$\mathrm{J}\left({r},\theta\right)=\frac{\partial\left({r},\theta\right)}{\partial\left({x},{y}\right)}=\begin{vmatrix}{\frac{\partial{x}}{\partial{r}}}&{\frac{\partial{x}}{\partial\theta}}\\{\frac{\partial{y}}{\partial{r}}}&{\frac{\partial{y}}{\partial\theta}}\end{vmatrix} \\ $$$${dxdy}=\mid\mathrm{J}\left({r},\theta\right)\mid{drd}\theta \\ $$

Commented by Filup last updated on 22/Nov/15

I have no idea what that is. It seems I have some research to conduct

$$\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{idea}\:\mathrm{what}\:\mathrm{that}\:\mathrm{is}.\:\mathrm{It}\:\mathrm{seems} \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{some}\:\mathrm{research}\:\mathrm{to}\:\mathrm{conduct} \\ $$

Commented by 123456 last updated on 22/Nov/15

its like a subtituition method for multivariable integral ∫_0 ^(+∞) e^(−r^2 ) rdr u=−r^2 ,du=−2rdr r=0⇒u=0 r→∞⇒u→−∞ −(1/2)∫_0 ^(−∞) e^u du=(1/2)∫_(−∞) ^0 e^u du=1/2 the jacobian generalize above idea to multivariable integrais like ∫_0 ^1 ∫_0 ^1 (x+y)(x−y)dxdy u=x+y v=x−y ∫∫_D uv ∣J(u,v)∣dudv

$$\mathrm{its}\:\mathrm{like}\:\mathrm{a}\:\mathrm{subtituition}\:\mathrm{method}\:\mathrm{for}\:\mathrm{multivariable}\:\mathrm{integral} \\ $$$$\underset{\mathrm{0}} {\overset{+\infty} {\int}}{e}^{−{r}^{\mathrm{2}} } {rdr} \\ $$$${u}=−{r}^{\mathrm{2}} ,{du}=−\mathrm{2}{rdr} \\ $$$${r}=\mathrm{0}\Rightarrow{u}=\mathrm{0} \\ $$$${r}\rightarrow\infty\Rightarrow{u}\rightarrow−\infty \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{−\infty} {\int}}{e}^{{u}} {du}=\frac{\mathrm{1}}{\mathrm{2}}\underset{−\infty} {\overset{\mathrm{0}} {\int}}{e}^{{u}} {du}=\mathrm{1}/\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{jacobian}\:\mathrm{generalize}\:\mathrm{above}\:\mathrm{idea}\:\mathrm{to} \\ $$$$\mathrm{multivariable}\:\mathrm{integrais}\:\mathrm{like} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}+{y}\right)\left({x}−{y}\right){dxdy} \\ $$$${u}={x}+{y} \\ $$$${v}={x}−{y} \\ $$$$\int\underset{\mathrm{D}} {\int}{uv}\:\mid\mathrm{J}\left({u},{v}\right)\mid{dudv} \\ $$

Commented by Filup last updated on 22/Nov/15

I just went and did a quick run−through. J(r,θ)=((∂(r,θ))/(∂(x,y)))= determinant (((∂x/∂r),(∂x/∂θ)),((∂y/∂r),(∂y/∂θ))) D=det(J(r,θ))=(∂x/∂r) (∂x/∂r)−(∂y/∂r) (∂y/∂θ)=r ∴∫∫e^(−x^2 −y^2 ) dxdy = ∫∫De^(−x^2 −y^2 ) drdθ =∫∫re^(−r^2 ) drdθ ?

$$\mathrm{I}\:\mathrm{just}\:\mathrm{went}\:\mathrm{and}\:\mathrm{did}\:\mathrm{a}\:\mathrm{quick}\:\mathrm{run}−\mathrm{through}. \\ $$$$ \\ $$$${J}\left({r},\theta\right)=\frac{\partial\left({r},\theta\right)}{\partial\left({x},{y}\right)}=\begin{vmatrix}{\frac{\partial{x}}{\partial{r}}}&{\frac{\partial{x}}{\partial\theta}}\\{\frac{\partial{y}}{\partial{r}}}&{\frac{\partial{y}}{\partial\theta}}\end{vmatrix} \\ $$$${D}={det}\left({J}\left({r},\theta\right)\right)=\frac{\partial{x}}{\partial{r}}\:\frac{\partial{x}}{\partial{r}}−\frac{\partial{y}}{\partial{r}}\:\frac{\partial{y}}{\partial\theta}={r} \\ $$$$ \\ $$$$\therefore\int\int{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {dxdy}\:=\:\int\int{De}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } {drd}\theta \\ $$$$=\int\int{re}^{−{r}^{\mathrm{2}} } {drd}\theta \\ $$$$? \\ $$

Commented by Filup last updated on 22/Nov/15

How do you determine the new limits?

$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{new}\:\mathrm{limits}? \\ $$

Commented by 123456 last updated on 22/Nov/15

−r^2 −x^2 −y^2 =−r^2 (cos^2 θ+sin^2 θ)=−r^2

$$−{r}^{\mathrm{2}} \\ $$$$−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =−{r}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta\right)=−{r}^{\mathrm{2}} \\ $$

Commented by 123456 last updated on 22/Nov/15

its a bit complex (mr.prakash could explain it better to you later) 0≤x<+∞∧0≤y<+∞ this limit give all the real plane R^2 in the new cordinates (polar) the same region is givd by 0≤r<+∞∧0≤θ<2π the radius varry fom 0 to +∞ and you rotate its to get the full R^2 in general drawing your region could help you to change the variables.

$$\mathrm{its}\:\mathrm{a}\:\mathrm{bit}\:\mathrm{complex}\:\left(\mathrm{mr}.\mathrm{prakash}\:\mathrm{could}\:\mathrm{explain}\:\mathrm{it}\:\mathrm{better}\:\mathrm{to}\:\mathrm{you}\:\mathrm{later}\right) \\ $$$$\mathrm{0}\leqslant{x}<+\infty\wedge\mathrm{0}\leqslant{y}<+\infty \\ $$$$\mathrm{this}\:\mathrm{limit}\:\mathrm{give}\:\mathrm{all}\:\mathrm{the}\:\mathrm{real}\:\mathrm{plane}\:\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{new}\:\mathrm{cordinates}\:\left(\mathrm{polar}\right)\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{region}\:\mathrm{is}\:\mathrm{givd}\:\mathrm{by} \\ $$$$\mathrm{0}\leqslant{r}<+\infty\wedge\mathrm{0}\leqslant\theta<\mathrm{2}\pi \\ $$$$\mathrm{the}\:\mathrm{radius}\:\mathrm{varry}\:\mathrm{fom}\:\mathrm{0}\:\mathrm{to}\:+\infty\:\mathrm{and}\:\mathrm{you} \\ $$$$\mathrm{rotate}\:\mathrm{its}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{full}\:\mathbb{R}^{\mathrm{2}} \\ $$$$\mathrm{in}\:\mathrm{general}\:\mathrm{drawing}\:\mathrm{your}\:\mathrm{region}\:\mathrm{could} \\ $$$$\mathrm{help}\:\mathrm{you}\:\mathrm{to}\:\mathrm{change}\:\mathrm{the}\:\mathrm{variables}. \\ $$

Commented by Filup last updated on 22/Nov/15

Whoops! Thanks for pointing out that typo. Ok, I understand now! I have done minimal work on matricies but I worked it all out just now! Thank you for helping me! The limits are probably the most confusing right now. I′ll look into it!

$${Whoops}!\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{pointing}\:\mathrm{out}\:\mathrm{that} \\ $$$$\mathrm{typo}.\:\mathrm{Ok},\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}!\: \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{have}\:\mathrm{done}\:\mathrm{minimal}\:\mathrm{work}\:\mathrm{on}\:\mathrm{matricies} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{worked}\:\mathrm{it}\:\mathrm{all}\:\mathrm{out}\:\mathrm{just}\:\mathrm{now}! \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{helping}\:\mathrm{me}! \\ $$$$ \\ $$$${The}\:\mathrm{limits}\:\mathrm{are}\:\mathrm{probably}\:\mathrm{the}\:\mathrm{most}\:\mathrm{confusing} \\ $$$$\mathrm{right}\:\mathrm{now}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{look}\:\mathrm{into}\:\mathrm{it}! \\ $$$$ \\ $$

Commented by Filup last updated on 22/Nov/15

I figured out what i was misunderstanding about the limits ∫_0 ^( ∞) re^(−r^2 ) dr→ −(1/2)∫_0 ^∞ −2re^(−r^2 ) dr u=−r^2 , du=−2rdr r=∞, u=−∞ r=0, u=0 =−(1/2)∫_0 ^(−∞) e^u du =(1/2)∫_(−∞) ^0 e^u du Simple problem now understood!

$$\mathrm{I}\:\mathrm{figured}\:\mathrm{out}\:\mathrm{what}\:\mathrm{i}\:\mathrm{was}\:\mathrm{misunderstanding} \\ $$$$\mathrm{about}\:\mathrm{the}\:\mathrm{limits} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {re}^{−{r}^{\mathrm{2}} } {dr}\rightarrow\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\infty} {\int}}−\mathrm{2}{re}^{−{r}^{\mathrm{2}} } {dr} \\ $$$${u}=−{r}^{\mathrm{2}} ,\:\:{du}=−\mathrm{2}{rdr} \\ $$$${r}=\infty,\:{u}=−\infty \\ $$$${r}=\mathrm{0},\:{u}=\mathrm{0} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{−\infty} {\int}}{e}^{{u}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{−\infty} {\overset{\mathrm{0}} {\int}}{e}^{{u}} {du} \\ $$$$ \\ $$$$\mathrm{Simple}\:\mathrm{problem}\:\mathrm{now}\:\mathrm{understood}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com