Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 25378 by Tinkutara last updated on 09/Dec/17

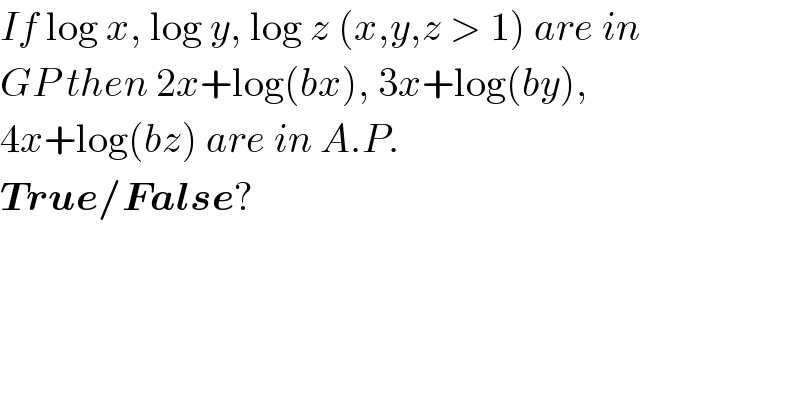
If log x, log y, log z (x,y,z > 1) are in GP then 2x+log(bx), 3x+log(by), 4x+log(bz) are in A.P. True/False?

$${If}\:\mathrm{log}\:{x},\:\mathrm{log}\:{y},\:\mathrm{log}\:{z}\:\left({x},{y},{z}\:>\:\mathrm{1}\right)\:{are}\:{in} \\ $$ $${GP}\:{then}\:\mathrm{2}{x}+\mathrm{log}\left({bx}\right),\:\mathrm{3}{x}+\mathrm{log}\left({by}\right), \\ $$ $$\mathrm{4}{x}+\mathrm{log}\left({bz}\right)\:{are}\:{in}\:{A}.{P}. \\ $$ $$\boldsymbol{{True}}/\boldsymbol{{False}}? \\ $$

Answered by Rasheed.Sindhi last updated on 09/Dec/17

((log y)/(log x))=((log z)/(log y)) Given To be proved: {3x+log(by)}−{2x+log(bx)} ={4x+log(bz)}−{3x+log(by)} x+log(by)−log(bx)=x+log(bz)−log(by) x+log(((by)/(bx)))=x+log(((bz)/(by))) log((y/x))=log((z/y)) log y−log x=log z−log y ∴ log x,log y, logz are in AP We can also prove vice versa i-e If log x,log y, logz are in AP then 2x+... , 3x+... , 4x+... are also in AP. ∴ If log x,log y, logz are in GP then 2x+..,3x+..,4x+... can′t be in GP (∵ a sequence can′t be both AP and GP simultneously in general.) Hence False.

$$\frac{\mathrm{log}\:{y}}{\mathrm{log}\:{x}}=\frac{\mathrm{log}\:{z}}{\mathrm{log}\:{y}}\:\:\:\mathrm{Given} \\ $$ $$\mathrm{To}\:\mathrm{be}\:\mathrm{proved}: \\ $$ $$\left\{\mathrm{3}{x}+\mathrm{log}\left({by}\right)\right\}−\left\{\mathrm{2}{x}+\mathrm{log}\left({bx}\right)\right\} \\ $$ $$\:\:\:\:\:=\left\{\mathrm{4}{x}+\mathrm{log}\left({bz}\right)\right\}−\left\{\mathrm{3}{x}+\mathrm{log}\left({by}\right)\right\} \\ $$ $${x}+\mathrm{log}\left({by}\right)−\mathrm{log}\left({bx}\right)={x}+\mathrm{log}\left({bz}\right)−\mathrm{log}\left({by}\right) \\ $$ $${x}+\mathrm{log}\left(\frac{{by}}{{bx}}\right)={x}+\mathrm{log}\left(\frac{{bz}}{{by}}\right) \\ $$ $$\mathrm{log}\left(\frac{{y}}{{x}}\right)=\mathrm{log}\left(\frac{{z}}{{y}}\right) \\ $$ $$\mathrm{log}\:\mathrm{y}−\mathrm{log}\:\mathrm{x}=\mathrm{log}\:\mathrm{z}−\mathrm{log}\:\mathrm{y}\:\: \\ $$ $$\therefore\:\mathrm{log}\:\mathrm{x},\mathrm{log}\:\mathrm{y},\:\mathrm{logz}\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP} \\ $$ $$\mathrm{We}\:\mathrm{can}\:\mathrm{also}\:\mathrm{prove}\:\mathrm{vice}\:\mathrm{versa} \\ $$ $$\mathrm{i}-\mathrm{e}\:\mathrm{If}\:\mathrm{log}\:\mathrm{x},\mathrm{log}\:\mathrm{y},\:\mathrm{logz}\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP} \\ $$ $$\mathrm{then}\:\mathrm{2x}+...\:,\:\mathrm{3x}+...\:,\:\mathrm{4x}+...\:\mathrm{are}\: \\ $$ $$\mathrm{also}\:\mathrm{in}\:\mathrm{AP}. \\ $$ $$\therefore\:\mathrm{If}\:\mathrm{log}\:\mathrm{x},\mathrm{log}\:\mathrm{y},\:\mathrm{logz}\:\mathrm{are}\:\mathrm{in}\:\mathrm{GP} \\ $$ $$\mathrm{then}\:\mathrm{2x}+..,\mathrm{3x}+..,\mathrm{4x}+...\:\mathrm{can}'\mathrm{t}\:\mathrm{be} \\ $$ $$\mathrm{in}\:\mathrm{GP}\:\left(\because\:\mathrm{a}\:\mathrm{sequence}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{both}\right. \\ $$ $$\left.\mathrm{AP}\:\mathrm{and}\:\mathrm{GP}\:\mathrm{simultneously}\:\mathrm{in}\:\mathrm{general}.\right) \\ $$ $$\mathrm{Hence}\:\mathrm{False}. \\ $$

Commented byTinkutara last updated on 09/Dec/17

Thank you Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com