Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 25379 by A1B1C1D1 last updated on 09/Dec/17

lim_(x → 0) ((((1 + x)^a − 1)/x)) for a ∈ R Don′t using L′hospital rules.

$$\underset{\mathrm{x}\:\rightarrow\:\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left(\mathrm{1}\:+\:\mathrm{x}\right)^{\mathrm{a}} \:−\:\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{for}\:\mathrm{a}\:\in\:\mathbb{R} \\ $$$$ \\ $$$$\mathrm{Don}'\mathrm{t}\:\mathrm{using}\:\mathrm{L}'\mathrm{hospital}\:\mathrm{rules}. \\ $$

Answered by Rasheed.Sindhi last updated on 10/Dec/17

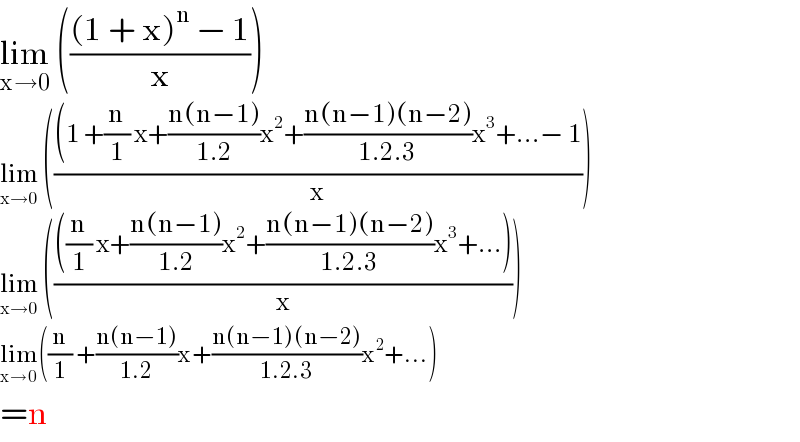
lim_(x→0) ((((1 + x)^n − 1)/x)) lim_(x→0) ((((1 +(n/1) x+((n(n−1))/(1.2))x^2 +((n(n−1)(n−2))/(1.2.3))x^3 +...− 1)/x)) lim_(x→0) (((((n/1) x+((n(n−1))/(1.2))x^2 +((n(n−1)(n−2))/(1.2.3))x^3 +...))/x)) lim_(x→0) ((n/1) +((n(n−1))/(1.2))x+((n(n−1)(n−2))/(1.2.3))x^2 +...) =n

$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left(\mathrm{1}\:+\:\mathrm{x}\right)^{\mathrm{n}} \:−\:\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left(\mathrm{1}\:+\frac{\mathrm{n}}{\mathrm{1}}\:\mathrm{x}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\mathrm{x}^{\mathrm{3}} +...−\:\mathrm{1}\right.}{\mathrm{x}}\right) \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left(\frac{\mathrm{n}}{\mathrm{1}}\:\mathrm{x}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\mathrm{x}^{\mathrm{3}} +...\right)}{\mathrm{x}}\right) \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{n}}{\mathrm{1}}\:+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{1}.\mathrm{2}}\mathrm{x}+\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\mathrm{x}^{\mathrm{2}} +...\right) \\ $$$$=\mathrm{n} \\ $$

Commented by A1B1C1D1 last updated on 09/Dec/17

Thank you

$$\mathrm{Thank}\:\mathrm{you} \\ $$

Answered by moxhix last updated on 10/Dec/17

another way put f(x)=(1+x)^a f ′(x)=a(1+x)^(a−1) →f ′(0)=a f ′(0)=lim_(x→0) (((1+x)^a −(1+0)^a )/(x−0)) ∴lim_(x→0) (((1+x)^a −1)/x)=a

$${another}\:{way} \\ $$$${put}\:{f}\left({x}\right)=\left(\mathrm{1}+{x}\right)^{{a}} \\ $$$${f}\:'\left({x}\right)={a}\left(\mathrm{1}+{x}\right)^{{a}−\mathrm{1}} \rightarrow{f}\:'\left(\mathrm{0}\right)={a} \\ $$$${f}\:'\left(\mathrm{0}\right)=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\left(\mathrm{1}+{x}\right)^{{a}} −\left(\mathrm{1}+\mathrm{0}\right)^{{a}} }{{x}−\mathrm{0}} \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\left(\mathrm{1}+{x}\right)^{{a}} −\mathrm{1}}{{x}}={a} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com