Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 2545 by Rasheed Soomro last updated on 22/Nov/15

Prove that 3^(3n) −26n−1 is divisible by 676, where n∈Z^+

$$\mathcal{P}{rove}\:{that}\:\mathrm{3}^{\mathrm{3}{n}} −\mathrm{26}{n}−\mathrm{1}\:{is}\:{divisible}\:{by}\:\mathrm{676}, \\ $$$${where}\:{n}\in\mathbb{Z}^{+} \\ $$

Commented by Yozzi last updated on 22/Nov/15

Use induction.

$${Use}\:{induction}. \\ $$

Answered by Yozzi last updated on 22/Nov/15

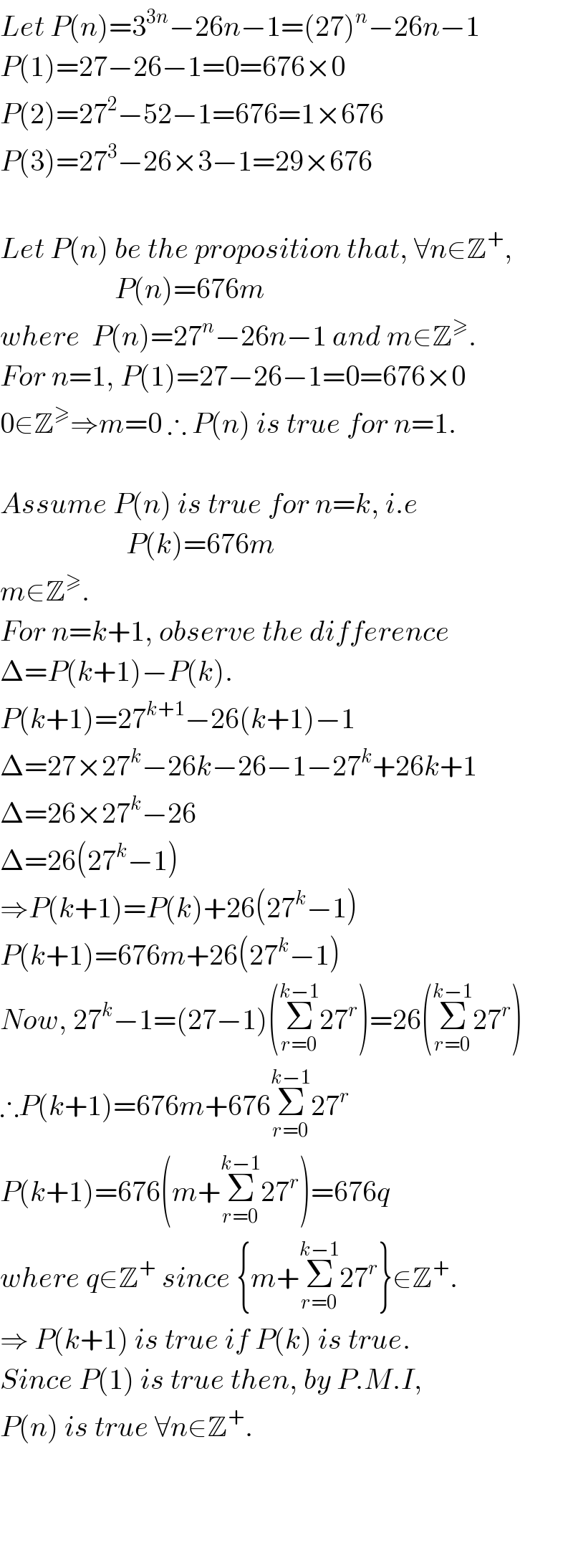
Let P(n)=3^(3n) −26n−1=(27)^n −26n−1 P(1)=27−26−1=0=676×0 P(2)=27^2 −52−1=676=1×676 P(3)=27^3 −26×3−1=29×676 Let P(n) be the proposition that, ∀n∈Z^+ , P(n)=676m where P(n)=27^n −26n−1 and m∈Z^≥ . For n=1, P(1)=27−26−1=0=676×0 0∈Z^≥ ⇒m=0 ∴ P(n) is true for n=1. Assume P(n) is true for n=k, i.e P(k)=676m m∈Z^≥ . For n=k+1, observe the difference Δ=P(k+1)−P(k). P(k+1)=27^(k+1) −26(k+1)−1 Δ=27×27^k −26k−26−1−27^k +26k+1 Δ=26×27^k −26 Δ=26(27^k −1) ⇒P(k+1)=P(k)+26(27^k −1) P(k+1)=676m+26(27^k −1) Now, 27^k −1=(27−1)(Σ_(r=0) ^(k−1) 27^r )=26(Σ_(r=0) ^(k−1) 27^r ) ∴P(k+1)=676m+676Σ_(r=0) ^(k−1) 27^r P(k+1)=676(m+Σ_(r=0) ^(k−1) 27^r )=676q where q∈Z^+ since {m+Σ_(r=0) ^(k−1) 27^r }∈Z^+ . ⇒ P(k+1) is true if P(k) is true. Since P(1) is true then, by P.M.I, P(n) is true ∀n∈Z^+ .

$${Let}\:{P}\left({n}\right)=\mathrm{3}^{\mathrm{3}{n}} −\mathrm{26}{n}−\mathrm{1}=\left(\mathrm{27}\right)^{{n}} −\mathrm{26}{n}−\mathrm{1} \\ $$$${P}\left(\mathrm{1}\right)=\mathrm{27}−\mathrm{26}−\mathrm{1}=\mathrm{0}=\mathrm{676}×\mathrm{0} \\ $$$${P}\left(\mathrm{2}\right)=\mathrm{27}^{\mathrm{2}} −\mathrm{52}−\mathrm{1}=\mathrm{676}=\mathrm{1}×\mathrm{676} \\ $$$${P}\left(\mathrm{3}\right)=\mathrm{27}^{\mathrm{3}} −\mathrm{26}×\mathrm{3}−\mathrm{1}=\mathrm{29}×\mathrm{676} \\ $$$$ \\ $$$${Let}\:{P}\left({n}\right)\:{be}\:{the}\:{proposition}\:{that},\:\forall{n}\in\mathbb{Z}^{+} , \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{P}\left({n}\right)=\mathrm{676}{m} \\ $$$${where}\:\:{P}\left({n}\right)=\mathrm{27}^{{n}} −\mathrm{26}{n}−\mathrm{1}\:{and}\:{m}\in\mathbb{Z}^{\geqslant} . \\ $$$${For}\:{n}=\mathrm{1},\:{P}\left(\mathrm{1}\right)=\mathrm{27}−\mathrm{26}−\mathrm{1}=\mathrm{0}=\mathrm{676}×\mathrm{0} \\ $$$$\mathrm{0}\in\mathbb{Z}^{\geqslant} \Rightarrow{m}=\mathrm{0}\:\therefore\:{P}\left({n}\right)\:{is}\:{true}\:{for}\:{n}=\mathrm{1}. \\ $$$$ \\ $$$${Assume}\:{P}\left({n}\right)\:{is}\:{true}\:{for}\:{n}={k},\:{i}.{e} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{P}\left({k}\right)=\mathrm{676}{m} \\ $$$${m}\in\mathbb{Z}^{\geqslant} . \\ $$$${For}\:{n}={k}+\mathrm{1},\:{observe}\:{the}\:{difference} \\ $$$$\Delta={P}\left({k}+\mathrm{1}\right)−{P}\left({k}\right).\: \\ $$$${P}\left({k}+\mathrm{1}\right)=\mathrm{27}^{{k}+\mathrm{1}} −\mathrm{26}\left({k}+\mathrm{1}\right)−\mathrm{1} \\ $$$$\Delta=\mathrm{27}×\mathrm{27}^{{k}} −\mathrm{26}{k}−\mathrm{26}−\mathrm{1}−\mathrm{27}^{{k}} +\mathrm{26}{k}+\mathrm{1} \\ $$$$\Delta=\mathrm{26}×\mathrm{27}^{{k}} −\mathrm{26} \\ $$$$\Delta=\mathrm{26}\left(\mathrm{27}^{{k}} −\mathrm{1}\right) \\ $$$$\Rightarrow{P}\left({k}+\mathrm{1}\right)={P}\left({k}\right)+\mathrm{26}\left(\mathrm{27}^{{k}} −\mathrm{1}\right) \\ $$$${P}\left({k}+\mathrm{1}\right)=\mathrm{676}{m}+\mathrm{26}\left(\mathrm{27}^{{k}} −\mathrm{1}\right) \\ $$$${Now},\:\mathrm{27}^{{k}} −\mathrm{1}=\left(\mathrm{27}−\mathrm{1}\right)\left(\underset{{r}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\mathrm{27}^{{r}} \right)=\mathrm{26}\left(\underset{{r}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\mathrm{27}^{{r}} \right) \\ $$$$\therefore{P}\left({k}+\mathrm{1}\right)=\mathrm{676}{m}+\mathrm{676}\underset{{r}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\mathrm{27}^{{r}} \\ $$$${P}\left({k}+\mathrm{1}\right)=\mathrm{676}\left({m}+\underset{{r}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\mathrm{27}^{{r}} \right)=\mathrm{676}{q} \\ $$$${where}\:{q}\in\mathbb{Z}^{+} \:{since}\:\left\{{m}+\underset{{r}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\mathrm{27}^{{r}} \right\}\in\mathbb{Z}^{+} . \\ $$$$\Rightarrow\:{P}\left({k}+\mathrm{1}\right)\:{is}\:{true}\:{if}\:{P}\left({k}\right)\:{is}\:{true}. \\ $$$${Since}\:{P}\left(\mathrm{1}\right)\:{is}\:{true}\:{then},\:{by}\:{P}.{M}.{I}, \\ $$$${P}\left({n}\right)\:{is}\:{true}\:\forall{n}\in\mathbb{Z}^{+} . \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 22/Nov/15

NICE^(Very) !

$$\overset{{Very}} {\boldsymbol{{NICE}}}\:! \\ $$

Answered by Rasheed Soomro last updated on 22/Nov/15

AN EASY Approach p(n): 3^(3n) −26n−1 is divisible by 676 Case−1_(−) :For n=1 3^(3n) −26n−1=3^3 −26−1=0 and 676∣0 Hence p(n) is true for n=1 Case−2 : Assume that for n=k , p(n) is true I−e 676 ∣ (3^(3k) −26k−1) Now for n=k+1, we have 3^(3(k+1)) −26(k+1)−1 =3^(3k+3) −26k−26−1 =27.3^(3k) −26k−27 =27.3^(3k) −27(26k)−27+26(26k) =27(3^(3k) −26k−1)+676k ∵ 676 ∣ (3^(3k) −26k−1) [By hypothesis]] and 676 ∣ 676k ∴ 676 ∣ 27(3^(3k) −26k−1)+676k ∴ p(n) is true for n=k+1,if it is true for n=k QED

$$\mathbb{AN}\:\:\:\mathcal{EASY}\:\boldsymbol{\mathrm{Approach}} \\ $$$$\boldsymbol{{p}}\left(\boldsymbol{{n}}\right):\:\:\:\mathrm{3}^{\mathrm{3}\boldsymbol{{n}}} −\mathrm{26}\boldsymbol{{n}}−\mathrm{1}\:\boldsymbol{{is}}\:\boldsymbol{{divisible}}\:\boldsymbol{{by}}\:\mathrm{676} \\ $$$$\underset{−} {\boldsymbol{{Case}}−\mathrm{1}}\::\boldsymbol{{F}}{or}\:\boldsymbol{{n}}=\mathrm{1} \\ $$$$\:\mathrm{3}^{\mathrm{3}\boldsymbol{{n}}} −\mathrm{26}\boldsymbol{{n}}−\mathrm{1}=\mathrm{3}^{\mathrm{3}} −\mathrm{26}−\mathrm{1}=\mathrm{0}\:\boldsymbol{{and}}\:\:\:\:\:\mathrm{676}\mid\mathrm{0} \\ $$$$\boldsymbol{{Hence}}\:\boldsymbol{{p}}\left(\boldsymbol{{n}}\right)\:\boldsymbol{{is}}\:\boldsymbol{{true}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\mathrm{1} \\ $$$$\boldsymbol{{Case}}−\mathrm{2}\::\:\boldsymbol{{Assume}}\:\boldsymbol{{that}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\boldsymbol{{k}}\:,\:\boldsymbol{{p}}\left(\boldsymbol{{n}}\right)\:\boldsymbol{{is}}\:\boldsymbol{{true}} \\ $$$$\boldsymbol{{I}}−\boldsymbol{{e}}\:\:\:\mathrm{676}\:\mid\:\left(\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}} −\mathrm{26}\boldsymbol{{k}}−\mathrm{1}\right) \\ $$$$\boldsymbol{{Now}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\boldsymbol{{k}}+\mathrm{1},\:\boldsymbol{{we}}\:\boldsymbol{{have}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{3}\left(\boldsymbol{{k}}+\mathrm{1}\right)} −\mathrm{26}\left(\boldsymbol{{k}}+\mathrm{1}\right)−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:=\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}+\mathrm{3}} −\mathrm{26}\boldsymbol{{k}}−\mathrm{26}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:=\mathrm{27}.\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}} −\mathrm{26}\boldsymbol{{k}}−\mathrm{27} \\ $$$$\:\:\:\:\:\:\:=\mathrm{27}.\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}} −\mathrm{27}\left(\mathrm{26}\boldsymbol{{k}}\right)−\mathrm{27}+\mathrm{26}\left(\mathrm{26}\boldsymbol{{k}}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{27}\left(\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}} −\mathrm{26}\boldsymbol{{k}}−\mathrm{1}\right)+\mathrm{676}\boldsymbol{{k}} \\ $$$$\left.\:\:\:\:\:\because\:\:\mathrm{676}\:\mid\:\left(\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}} −\mathrm{26}\boldsymbol{{k}}−\mathrm{1}\right)\:\left[\boldsymbol{{By}}\:\boldsymbol{{hypothesis}}\right]\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{and}}\:\mathrm{676}\:\mid\:\mathrm{676}\boldsymbol{{k}} \\ $$$$\:\:\:\:\:\:\therefore\:\mathrm{676}\:\mid\:\mathrm{27}\left(\mathrm{3}^{\mathrm{3}\boldsymbol{{k}}} −\mathrm{26}\boldsymbol{{k}}−\mathrm{1}\right)+\mathrm{676}\boldsymbol{{k}} \\ $$$$\therefore\:\:\boldsymbol{{p}}\left(\boldsymbol{{n}}\right)\:\boldsymbol{{is}}\:\boldsymbol{{true}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\boldsymbol{{k}}+\mathrm{1},\boldsymbol{{if}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{true}}\:\boldsymbol{{for}}\:\boldsymbol{{n}}=\boldsymbol{{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{QED}} \\ $$

Commented by Yozzi last updated on 22/Nov/15

Nicely □

$${Nicely}\:\:\Box \\ $$

Commented by Rasheed Soomro last updated on 23/Nov/15

□ THANKS! Actually I saw this problem and its solution in a book and wanted to share with friends on this platform. Therefore in order to get oppertunity I posted the question. I like your answer because its your own whereas my answer is bookish and not my own.Anyway it is such that it be shared.

$$\Box\:\mathcal{THANK}\mathbb{S}! \\ $$$${Actually}\:{I}\:{saw}\:{this}\:{problem}\:{and}\:{its}\:{solution}\:{in}\:{a}\:{book} \\ $$$${and}\:{wanted}\:{to}\:{share}\:{with}\:{friends}\:{on}\:{this}\:{platform}. \\ $$$${Therefore}\:{in}\:{order}\:{to}\:{get}\:{oppertunity}\:{I}\:{posted}\:{the}\:{question}. \\ $$$$\:\:\:\:\:\mathcal{I}\:{like}\:{your}\:{answer}\:{because}\:{its}\:{your}\:{own}\:{whereas}\:{my} \\ $$$${answer}\:{is}\:{bookish}\:{and}\:{not}\:{my}\:{own}.{Anyway}\:{it}\:{is}\:{such}\:{that} \\ $$$${it}\:{be}\:{shared}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com